SVM的基础原理

因为看cs231的时候用了一下multi-class的svm，所以又把svm给复习了一下，教材是周志华的西瓜书，这里是大概的笔记。

1.线性可分

对于一个数据集：

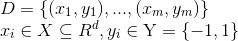
如果存在一个超平面X能够将D中的正负样本精确地划分到S的两侧，超平面如下：

那么数据集D就是线性可分的，否则，不可分。

w称为法向量，决定了超平面的方向；b为位移量，决定了超平面与原点的距离。

样本空间中的任意点x到超平面X的距离（不太熟悉的可以复习高数中空间几何那一章的内容）可以写为：

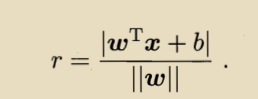
使得下面两式成立的训练样本称为支持向量：

两个异类支持向量（一个等于+1，一个等于-1）到超平面的距离之和为:

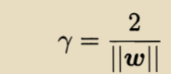
它称之为“间隔”

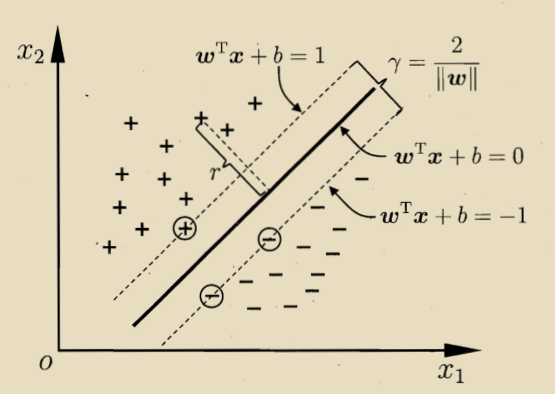
想找到最大间隔的划分超平面，就是使最大：

等价于：

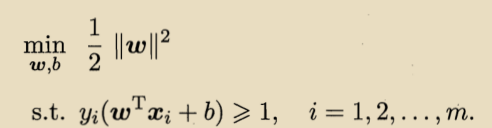
这就是支持向量机的基本模型。

对偶问题：

上式的拉格朗日函数可写为：

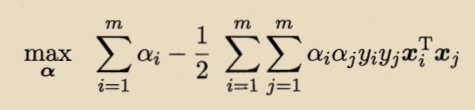
其中，

对参数w和b求导可得：

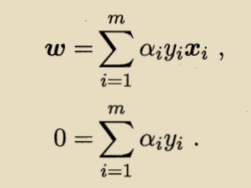
将上式带入到拉格朗日函数中，消去w和b,得到对偶表达式：

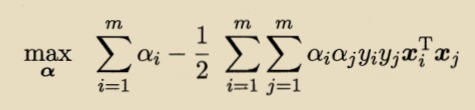
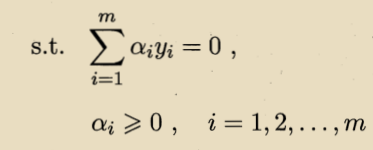
接着用SMO的方法来求解

接着求B，因为根据我们的受限条件，任意一个支持向量都可以计算b，但是为了模型的鲁棒性，接着我们把所有的支持向量来求平均

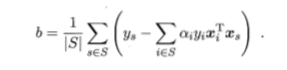
其中S为支持向量集