可持久化数据结构QwQ(持续更新中)
可持久化留下的迹象 我们俯身欣赏
——《膜你抄》By Menci&24OI
Micardi最近在学可持久化的东西,可持久化线段树、可持久化并查集、可持久化01Trie......等等等等恶心人的东西QwQ。不过呢,犯其至难,图其至远,如果能静下心来搞定这些乱七八糟的玩意,相信对自己的OI之路也会大有裨益吧QwQ。
(不过照Micardi的尿性这或许会是一篇更不完的博文QwQ)
言归正传!
1.主席树(可持久化线段树)
属于Micardi的数据结构!
什么是主席树?
主席树,本名可持久化线段树——顾名思义,它是一种基于线段树、并且可持久的一种数据结构。为什么要叫主席树?因为它是由一位名叫黄嘉泰的巨佬发明的......而这位巨佬的名字缩写对应了前国家主席2333333因此得名。主席树还有个名字叫函数式线段树,这我们就不用去管因为什么了因为我也不太懂啊QAQ......
主席树怎么用?
来,让我们步入正题:
Q1:给出序列an,你需要对该序列进行两种操作:1.在某一历史版本基础上修改某个元素值;2.查询某一历史版本里的某一元素值。我们定义初始序列为版本0,每进行一次操作都会生成一个新的版本。序列内元素个数n、操作数m均≤5×106。
单点修改+单点查询,很自然地,我们想到了线段树、树状数组(分块、莫队、splay)......于是最暴力的做法显而易见:每一个版本我们都建立一颗线段树,然后模拟修改和查询。时间复杂度O(mnlogn),显然无法承受——而且m棵线段树,真的不怕赤果果的MLE嘛?
这个时候,我们就要搬出我们的主席树啦!
我们考虑这样一个问题:从算法正确性上考虑,不停地建立线段树——是对的,我们需要做的是优化这种做法可怕的时空复杂度。如何优化呢?我们要从线段树特点上下手啦:
假设已知序列1,2,3,4,5,我们建一颗线段树:
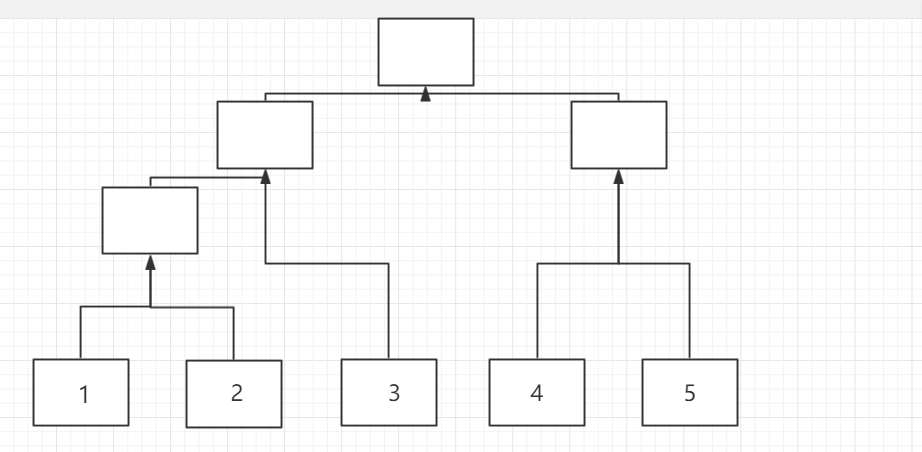
如果我们现在要修改3,会有哪些节点被修改呢?
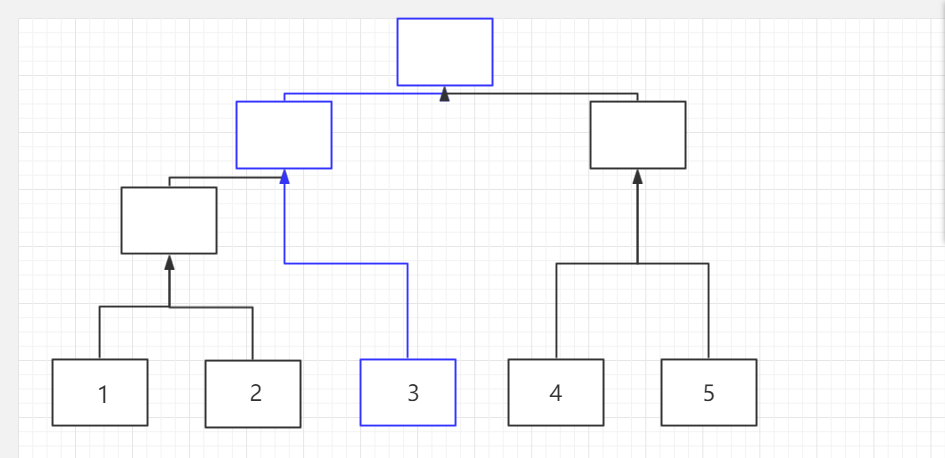
很显然啦,只有这个叶子节点到树根一条路上的节点会被修改——深入思考一下不难发现,对于每一次单点修改,我们其实只需要修改它->它爸->它爷爷->......->树根这些节点。由于线段树是一颗平衡二叉树,树高差不多就是logn(这么不严谨应该拖出去打死)所以我们每次只需要修改logn个节点即可——完全用不着再重新建一整颗线段树。
可是我们怎么知道要改哪些呢?——画画图也不难发现,由于线段树每一个节点左儿子的sum存储的是该节点对应区间左半边的信息,右儿子存储的是右半边的信息,假设我们要修改的位置是x,那么如果x在左半边(即x<=mid)我们就去修改左子树,保留右子树,反之亦然。这样从根节点递归到叶子结点,我们就可以完成一次修改啦:
#include<bits/stdc++.h>
#define mid ((l+r)/2)
using namespace std; const int N=; int sum[N<<],L[N<<],R[N<<],rt[N<<],a[N],cnt;
int n,m; int build(int l,int r)
{
int rt=++cnt;
if(l==r)
{
sum[rt]=a[l];
return rt;
}
L[rt]=build(l,mid);R[rt]=build(mid+,r);
return rt;
} int upd(int pre,int l,int r,int x,int v)//把第pre个版本修改成v
{
int rt=++cnt;
L[rt]=L[pre],R[rt]=R[pre],sum[rt]=sum[pre];
if(l==r){sum[rt]=v;return rt;}
if(x<=mid)L[rt]=upd(L[pre],l,mid,x,v);
else R[rt]=upd(R[pre],mid+,r,x,v);
return rt;
} int query(int pre,int l,int r,int x)
{
if(l==r)return sum[pre];
if(x<=mid)return query(L[pre],l,mid,x);
else return query(R[pre],mid+,r,x);
} int main()
{
scanf("%d%d",&n,&m);
for(register int i=;i<=n;++i)scanf("%d",&a[i]);
rt[]=build(,n);
for(register int i=;i<=m;++i)
{
int opt,x,y;
scanf("%d%d%d",&x,&opt,&y);
if(opt==)
{
int z;scanf("%d",&z);
rt[i]=upd(rt[x],,n,y,z);
}
else
{
rt[i]=rt[x];
printf("%d\n",query(rt[x],,n,y));
}
}
return ;
}
Q2:给出序列an,查询区间第k小值。序列长度n、查询次数m均≤2×105。
静态区间第k小值......暴力倒是非常好写。O(mnlogn)随便搞就搞出来了——不过思考一下如何在时限内跑完呢?
我会莫队!我会整体二分!既然你讲主席树那么这一定要用主席树写!......
咳,这的确是主席树的经典模板之一。我们还是从一个栗子开始——3 2 1 4:
开始我先搞一颗空树:
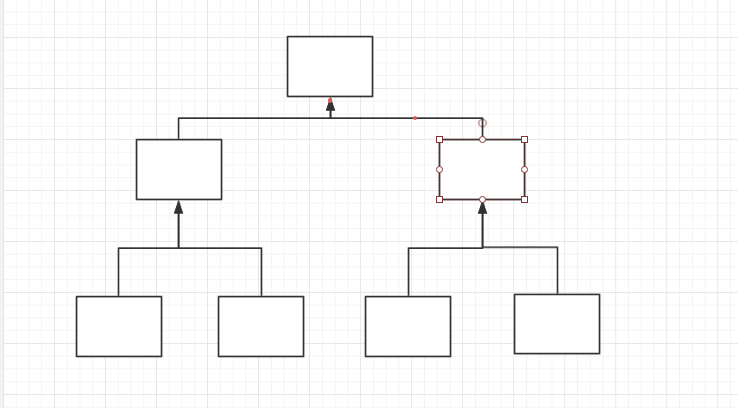
可持久化数据结构QwQ(持续更新中)的更多相关文章
- 史上最全的spark面试题——持续更新中
史上最全的spark面试题——持续更新中 2018年09月09日 16:34:10 为了九亿少女的期待 阅读数 13696更多 分类专栏: Spark 面试题 版权声明:本文为博主原创文章,遵循C ...
- Pig基础学习【持续更新中】
*本文参考了Pig官方文档以及已有的一些博客,并加上了自己的一些知识性的理解.目前正在持续更新中.* Pig作为一种处理大规模数据的高级查询语言,底层是转换成MapReduce实现的,可以作为MapR ...
- Pig语言基础-【持续更新中】
***本文参考了Pig官方文档以及已有的一些博客,并加上了自己的一些知识性的理解.目前正在持续更新中.*** Pig作为一种处理大规模数据的高级查询语言,底层是转换成MapReduce实现的, ...
- java视频教程 Java自学视频整理(持续更新中...)
视频教程,马士兵java视频教程,java视频 1.Java基础视频 <张孝祥JAVA视频教程>完整版[RMVB](东西网) 历经5年锤炼(史上最适合初学者入门的Java基础视频)(传智播 ...
- 《WCF技术剖析》博文系列汇总[持续更新中]
原文:<WCF技术剖析>博文系列汇总[持续更新中] 近半年以来,一直忙于我的第一本WCF专著<WCF技术剖析(卷1)>的写作,一直无暇管理自己的Blog.在<WCF技术剖 ...
- 白话kubernetes的十万个为什么(持续更新中...) - kubernetes
Kubernetes简称? 答:k8s或kube. Kubernetes是什么? 答:由Google开发的一个强大的平台,可以在集群环境中管理容器化应用程序.本质上是一种特殊的数据库,里面存储的是能够 ...
- 前端深入之js篇丨Array数组操作从入门到成神Up Up Up,持续更新中
写在前面 随着前端深入的不断学习,发现数组这个数据结构在前端中有着相当大的存在感,由于我初学前端的时候并没有系统性的学习数组,所以我将通过这篇文章同你一起学习数组,希望我们能一起进步,学会熟练操作数组 ...
- 2020年腾讯实习生C++面试题&持续更新中(2)
2020年腾讯实习生C++面试题&持续更新中(2) hello,大家好~ 我是好好学习天天,天天编程的天天,一个每天都死磕技术,及时分享的技术宅~ 昨天分享的题目不知道大家是否看过了,以后我计 ...
- 2020年腾讯实习生C++面试题&持续更新中(5)
2020年腾讯实习生C++面试题&持续更新中(5) 大家好呀,我是好好学习天天编程的天天~ 昨天一位小伙伴反馈已经拿到了腾讯offer,很是替小伙伴的激动~ 那今天还是持续给大家分享面经,希望 ...
- 【前端面试】Vue面试题总结(持续更新中)
Vue面试题总结(持续更新中) 题目参考链接 https://blog.csdn.net/weixin_45257157/article/details/106215158 由于已经有很多前辈深造VU ...
随机推荐
- Opencv 分水岭分割图片
#include <iostream>#include <opencv2/opencv.hpp> using namespace std;using namespace cv; ...
- 825. Friends Of Appropriate Ages有效的好友请求的数量
[抄题]: Some people will make friend requests. The list of their ages is given and ages[i] is the age ...
- 解决VS2013中的控制台一闪而过的问题
修改项目配置,右键点击项目,在右键菜单中选择属性,然后在弹出的对话框左侧列表中中选择 “配置属性”-->“链接器”-->“系统”,然后在右侧的列表中, 在第一项”子系统“的值中选择”控制台 ...
- linux zip解压缩中文乱码
这里提供两个解决方案: 1.python处理下:https://gist.github.com/wangjiezhe/7841a350983a147b6d7e 2.java的zip4j:http:// ...
- Windows查看端口占用及杀掉进程
"到底是谁占用了80端口,该怎么查,怎么终止它?",这里就简单讲解一下,在windows下如何查看80端口占用情况?是被哪个进程占用?如何终止等.这里主要是用到windows下的D ...
- 关于HBase的memstoreFlushSize。
memstoreFlushSize是什么呢? memstoreFlushSize为HRegion上设定的一个阈值,当MemStore的大小超过这个阈值时,将会发起flush请求. 它的计算首先是由Ta ...
- R Markdown 速查表
- centos7设置、查看、删除环境变量的方法
centos查看环境变量与设置环境变量在使用过程中很常见,本文整理了一些常用的与环境变量相关的命令,感兴趣的朋友可以参考下希望对你有所帮助 1. 显示环境变量HOME(红色部分代表要输入的命令,不要把 ...
- maven 引用本地jar
1.添加lib文件夹在src文件夹中.2.拷贝所需要的test.jar包到lib文件夹.3.在pom文件加入如下依赖 <!--添加本地私有包--><dependency> &l ...
- Jrebel 独立部署tomcat 远程同步项目
一直在用 jrebel 感觉热部署的 功能,修改xml配置文件等,省去了很多的重新启动的时间. 由于偶然间发现 jrebel 还有remote 路由功能.这样,在服务器端用jrebel部署的项目和本地 ...
