29-中国剩余定理CRT
中国剩余定理的具体描述是这样的:

给出你n个ai和mi,最后让求出x的最小值是多少。
中国剩余定理说明:假设整数m1, m2, ... , mn两两互质,则对任意的整数:a1, a2, ... , an,方程组 有解,并且通解可以用如下方式构造得到:
有解,并且通解可以用如下方式构造得到:
- 设
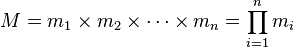 是整数m1, m2, ... , mn的乘积,并设
是整数m1, m2, ... , mn的乘积,并设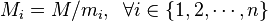 是除了mi以外的n - 1个整数的乘积。
是除了mi以外的n - 1个整数的乘积。 - 设
 为
为 模
模 的数论倒数:
的数论倒数:
- 方程组
 的通解形式为:
的通解形式为: 在模
在模 的意义下,方程组
的意义下,方程组 只有一个解:
只有一个解: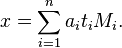
使用中国剩余定理来求解上面的“物不知数”问题,便可以理解《孙子歌诀》中的数字含义。这里的线性同余方程组是:
三个模数m1 3, m2
3, m2 5, m3
5, m3 7的乘积是M
7的乘积是M 105,对应的M1
105,对应的M1 35, M2
35, M2 21, M3
21, M3 15. 而可以计算出相应的数论倒数:t1
15. 而可以计算出相应的数论倒数:t1 2, t2
2, t2 1, t3
1, t3 1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:
1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:
而将原方程组中的余数相应地乘到这三个基础解上,再加起来,其和就是原方程组的解:
这个和是233,实际上原方程组的通解公式为:
《孙子算经》中实际上给出了最小正整数解,也就是k -2时的解:x
-2时的解:x 23.
23.
- ///n个mi互质
- const LL maxn = 20;
- LL a[maxn], m[maxn], n;
- LL CRT(LL a[], LL m[], LL n)
- {
- LL M = 1;
- for (int i = 0; i < n; i++) M *= m[i];
- LL ret = 0;
- for (int i = 0; i < n; i++)
- {
- LL x, y;
- LL tm = M / m[i];
- ex_gcd(tm, m[i], x, y);
- ret = (ret + tm * x * a[i]) % M;
- }
- return (ret + M) % M;
- }
分割线
- ///n个mi不互质
- const LL maxn = 1000;
- LL a[maxn], m[maxn], n;
- LL CRT(LL a[], LL m[], LL n) {
- if (n == 1) {
- if (m[0] > a[0]) return a[0];
- else return -1;
- }
- LL x, y, d;
- for (int i = 1; i < n; i++) {
- if (m[i] <= a[i]) return -1;
- d = ex_gcd(m[0], m[i], x, y);
- if ((a[i] - a[0]) % d != 0) return -1; //不能整除则无解
- LL t = m[i] / d;
- x = ((a[i] - a[0]) / d * x % t + t) % t; //第0个与第i个模线性方程的特解
- a[0] = x * m[0] + a[0];
- m[0] = m[0] * m[i] / d;
- a[0] = (a[0] % m[0] + m[0]) % m[0];
- }
- return a[0];
- }
以上大部分内容来自wiki
29-中国剩余定理CRT的更多相关文章
- 「中国剩余定理CRT」学习笔记
设正整数$m_1, m_2, ... , m_r$两两互素,对于同余方程组 $x ≡ a_1 \ (mod \ m_1)$ $x ≡ a_2 \ (mod \ m_2)$ $...$ $x ≡ a_r ...
- 中国剩余定理CRT(孙子定理)
中国剩余定理 给出以下的一元线性同余方程组: $\Large(s):\left\{\begin{aligned}x\equiv a_1\ (mod\ m_1)\\x\equiv a_2\ (mod\ ...
- 【bzoj3782】上学路线 dp+容斥原理+Lucas定理+中国剩余定理
题目描述 小C所在的城市的道路构成了一个方形网格,它的西南角为(0,0),东北角为(N,M).小C家住在西南角,学校在东北角.现在有T个路口进行施工,小C不能通过这些路口.小C喜欢走最短的路径到达目的 ...
- acm数论之旅--中国剩余定理
ACM数论之旅9---中国剩余定理(CRT)(壮哉我大中华╰(*°▽°*)╯) 中国剩余定理,又名孙子定理o(*≧▽≦)ツ 能求解什么问题呢? 问题: 一堆物品 3个3个分剩2个 5个5个分剩3个 ...
- 卢卡斯定理&&中国剩余定理
卢卡斯定理(模数较小,且是质数) 式子C(m,n)=C(m/p,n/p)*C(m%p,n%p)%p 至于证明(我也不会QAQ,只要记住公式也该就好了). 同时卢卡斯定理一般用于组合数取模上 1.首先当 ...
- gcd,扩展欧几里得,中国剩余定理
1.gcd: int gcd(int a,int b){ ?a:gcd(b,a%b); } 2.中国剩余定理: 题目:学生A依次给n个整数a[],学生B相应给n个正整数m[]且两两互素,老师提出问题: ...
- NOI 2018 屠龙勇士 (拓展中国剩余定理excrt+拓展欧几里得exgcd)
题目大意:略 真是一波三折的一道国赛题,先学了中国剩余定理,勉强看懂了模板然后写的这道题 把取出的宝剑攻击力设为T,可得Ti*x=ai(mod pi),这显然是ax=c(mod b)的形式 这部分用e ...
- POJ 1006:Biorhythms 中国剩余定理
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 121194 Accepted: 38157 Des ...
- RSA遇上中国剩余定理
1.Introduction 最近读论文刚好用到了这个,之前只是有耳闻,没有仔细研究过,这里就好好捋一下,会逐步完善 不过貌似CRT(中国剩余定理)的实现更容易被攻击 2. RSA: Overview ...
- 《孙子算经》之"物不知数"题:中国剩余定理
1.<孙子算经>之"物不知数"题 今有物不知其数,三三数之剩二,五五数之剩七,七七数之剩二,问物几何? 2.中国剩余定理 定义: 设 a,b,m 都是整数. 如果 m ...
随机推荐
- 网络流量监控分析工具 Ntopng 安装
官方说明:http://packages.ntop.org/ http://packages.ntop.org/centos-stable/ http://packages.ntop.o ...
- Oracle存储过程记录异常日志
一般我们会将一些涉及到数据库的定时任务直接用存储过程搞定,省去了后端代码的开发.部署,简单.快速,但这种方式存在一个弊端——当存储过程执行出错了,我们无法感知.解决办法也简单,学代码那样去捕获异常.打 ...
- C/S模式与B/
网络程序开发的两种计算模式--C/S模式与B/S模式.两种各有千秋,用于不同场合. C/S适用于专人使用,安全性要求较高的系统: B/S适用于交互性比较频繁的场合,容易被人们所接受,倍受用户和软件开发 ...
- 关于使用PyExecJS+nodejs使用与js反混淆
来源:https://cuiqingcai.com/5024.html 梳理这篇博客的时候出问题,我默认的是jscript作为pyexcJs的引擎,问题很大,大部分的js都无法加载,各种包用不了,只能 ...
- Docker for windows 7 - 加载 docker images
背景 由于之前一直是在 Linux 上面跑,所以对于docker for windows 部分不是很熟. 由于我们的合作伙伴需要在windows 上面跑我们的docker image, 所以在自己的w ...
- PyQt5+python+pycharm开发环境配置
Qt Designer的安装方法 使用Qt Designer可以使用GUI的方式快速生成PyQt代码,本文介绍Qt Designer的安装以及在PyCharm中的配置方法. pip install P ...
- htm标签的语意
标签名 英文全拼 标签语意 div division 分割 span span 范围 ol ordered list 排序列表 ul unordered list 不排序列表 li list item ...
- [安全分享]斗鱼&360补天沙龙分享-跨域资源那些事
[安全分享]斗鱼&360补天沙龙分享-跨域资源那些事 主要内容: 文件: http://scan.javasec.cn/补天&斗鱼-跨域资源那些事.pdf
- GridControl 添加全选列
这里通过List对象绑定GridControl,且不用在GirdControl界面中添加任何列,实现CheckBox列的方法 1.列表中出现CheckBox列 非常简单,在绑定的List实体中,增加一 ...
- 【Java】编程
3.Java I/O流输入输出,序列化,NIO,NIO.2 https://www.cnblogs.com/jiangwz/p/9193776.html 4.JAVA调用WCF(转) https:// ...



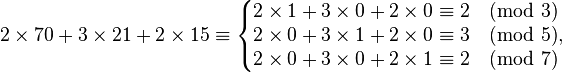

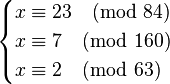 与
与 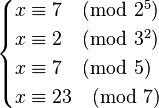 同解。
同解。