大白书 209 remember the word

F - Remember the Word

Time Limit:3000MS     Memory Limit:0KB     64bit IO Format:%lld & %llu

Submit Status Practice UVA 1401

Appoint description: 
System Crawler  (2015-03-07)

Description

 

Neal is very curious about combinatorial problems, and now here comes a problem about words. Knowing that Ray has a photographic memory and this may not trouble him, Neal gives it to Jiejie.

Since Jiejie can't remember numbers clearly, he just uses sticks to help himself. Allowing for Jiejie's only 20071027 sticks, he can only record the remainders of the numbers divided by total amount of sticks.

The problem is as follows: a word needs to be divided into small pieces in such a way that each piece is from some given set of words. Given a word and the set of words, Jiejie should calculate the number of ways the given word can be divided, using the words in the set.

Input

The input file contains multiple test cases. For each test case: the first line contains the given word whose length is no more than 300 000.

The second line contains an integer S<tex2html_verbatim_mark> , 1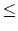S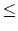4000<tex2html_verbatim_mark> .

Each of the following S<tex2html_verbatim_mark> lines contains one word from the set. Each word will be at most 100 characters long. There will be no two identical words and all letters in the words will be lowercase.

There is a blank line between consecutive test cases.

You should proceed to the end of file.

Output

For each test case, output the number, as described above, from the task description modulo 20071027.

Sample Input

abcd
4
a
b
cd
ab

Sample Output

Case 1: 2

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int ch[][],val[];
int sz,d[];
int idx(char c)
{
    return c-'a';
}
void insert(char *s,int v)
{
    int  u=,n=strlen(s);
    for(int i=;i<n;i++)
    {
        int c=idx(s[i]);
        if(!ch[u][c])
        {
            memset(ch[sz],,sizeof(ch[sz]));
            val[sz]=;
            ch[u][c]=sz++;
        }
        u=ch[u][c];
    }
    val[u]=v;
}
int main()
{
    char s[],a[];
     int  i,x,t=,j;
    while(~scanf("%s",s))
     {
         memset(d,,sizeof(d));
          sz=;
        memset(ch[],,sizeof(ch[]));
         scanf("%d",&x);
         for(i=;i<=x;i++)
         {
             scanf("%s",a);
             insert(a,-);
         }
         int root,i,j,k;
         int len=strlen(s);
          d[len]=;
       for(i=len-;i>=;i--)
        {
             root=;
          for(j=,k=i;k<len;j++,k++)
           {
             int c=idx(s[k]);
             if(ch[root][c]==)
                break;
             else if(val[ch[root][c]]==-)
             {
               d[i] += d[i+j+];
              if(d[i] >= ) d[i] %= ;
             }
              root=ch[root][c];
          }

     }
         printf("Case %d: %d\n",t++,d[]%);
     }
}