【网络流24题】No.4 魔术球问题 （二分+最小路径覆盖）

【题意】

　　假设有 n 根柱子， 现要按下述规则在这 n 根柱子中依次放入编号为 1， 2， 3， ¼的球。
（ 1）每次只能在某根柱子的最上面放球。
（ 2）在同一根柱子中，任何 2 个相邻球的编号之和为完全平方数。
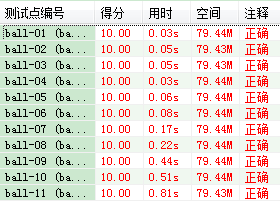
试设计一个算法， 计算出在 n 根柱子上最多能放多少个球。 例如，在 4 根柱子上最多可
放 11 个球。

输入文件示例
input.txt
4

输出文件示例

output.txt

11
1 8
2 7 9
3 6 10
4 5 11

【分析】

　　二分答案。然后连边u->v 表示v可以放在u后面，然后就是一个有向图的最小路径覆盖（点不能重复）

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<queue>
 #include<cmath>
 using namespace std;
 #define Maxn 4100
 #define INF 0xfffffff

 struct node
 {
     int x,y,f,o,next;
 }t[Maxn*];int len;
 int first[Maxn];

 int mymin(int x,int y) {return x<y?x:y;}

 void ins(int x,int y,int f)
 {
     t[++len].x=x;t[len].y=y;t[len].f=f;
     t[len].next=first[x];first[x]=len;t[len].o=len+;
     t[++len].x=y;t[len].y=x;t[len].f=;
     t[len].next=first[y];first[y]=len;t[len].o=len-;
 }

 int st,ed;
 queue<int > q;
 int dis[Maxn];
 bool bfs()
 {
     while(!q.empty()) q.pop();
     memset(dis,-,sizeof(dis));
     q.push(st);dis[st]=;
     while(!q.empty())
     {
         int x=q.front();
         for(int i=first[x];i;i=t[i].next) if(t[i].f>)
         {
             int y=t[i].y;
             if(dis[y]==-)
             {
                 dis[y]=dis[x]+;
                 q.push(y);
             }
         }
         q.pop();
     }
     if(dis[ed]==-) return ;
     return ;
 }

 int ffind(int x,int flow)
 {
     if(x==ed) return flow;
     int now=;
     for(int i=first[x];i;i=t[i].next) if(t[i].f>)
     {
         int y=t[i].y;
         if(dis[y]==dis[x]+)
         {
             int a=ffind(y,mymin(flow-now,t[i].f));
             t[i].f-=a;
             t[t[i].o].f+=a;
             now+=a;
         }
         if(now==flow) break;
     }
     if(now==) dis[x]=-;
     return now;
 }

 void output()
 {
     for(int i=;i<=len;i+=)
      printf("%d->%d %d\n",t[i].x,t[i].y,t[i].f);
 }

 int max_flow()
 {
     int ans=;
     while(bfs())
     {
         ans+=ffind(st,INF);
         // printf("--%d\n",ans);
         // output();
     }
     return ans;
 }

 int n;
 bool check(int x)
 {
     len=;
     memset(first,,sizeof(first));
     for(int i=;i<=x;i++)
      for(int j=i+;j<=x;j++)
      {
          int yy=i+j,y=(int)sqrt((double)yy);
          if(y*y==yy)
          {
              ins(i,j+x,);
          }
      }
     st=*x+;ed=st+;
     for(int i=;i<=x;i++) ins(st,i,);
     for(int i=;i<=x;i++) ins(i+x,ed,);
     // if(x==10) output();
     int y=max_flow();
     return x-y<=n;
 }

 int nt[Maxn];
 bool vis[Maxn];

 int main()
 {
     scanf("%d",&n);
     int l=,r=;
     while(l<r)
     {
         int mid=(l+r+)>>;
         if(check(mid)) l=mid;
         else r=mid-;
     }
     printf("%d\n",l);
     check(l);
     // output();
     memset(nt,,sizeof(nt));
     memset(vis,,sizeof(vis));
     for(int i=;i<=len;i+=) if(t[i].x!=st&&t[i].y!=ed&&t[i].f==)
         nt[t[i].x]=t[i].y-l,vis[t[i].y-l]=;
     for(int i=;i<=l;i++) if(vis[i])
     {
         int x=i;
         while(x)
         {
             printf("%d ",x);
             x=nt[x];
         }
         printf("\n");
     }
     return ;
 }

缓慢飘过~~

2016-11-04 10:45:42