[杂题]CSUOJ1413 Area of a Fractal

题目链接

题意：题中给了图，所以不看字大概也知道

　　  求的是第n个图形的面积。

就是找规律 递推 一类的...

先给结论：

很鬼畜的公式：    $\displaystyle\frac{3\times 17^n+2\times 7^n}{5}$

递推式是:  $\displaystyle S_n = S_{n-1}\times 17-4\times 7^{n-1}$

重点在于17和7是怎么来的。

在题图的基础上画些个框框

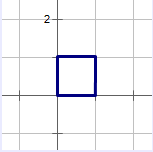
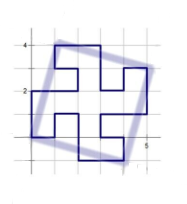
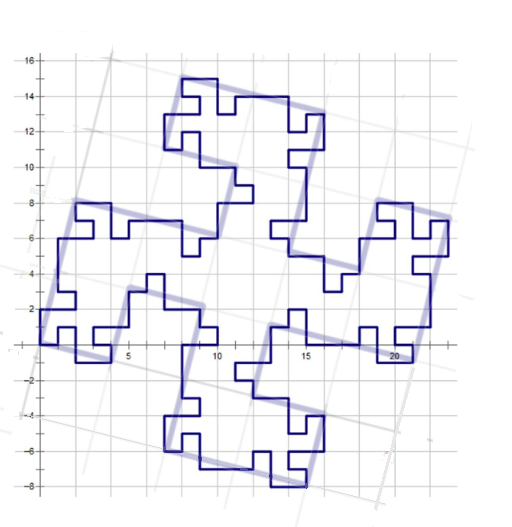
观察可以发现 图1中的 $1\times 1$的方格变成了图2中$\sqrt{17}\times \sqrt{17}$的方格

　　　　其中17就是$4\times 4 + 1\times 1$

所以第二个方格的面积为前一个方格的17倍。

显然17倍了之后还不是该图形的面积，因为有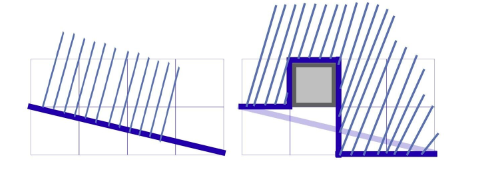（灰格子）的面积少了。

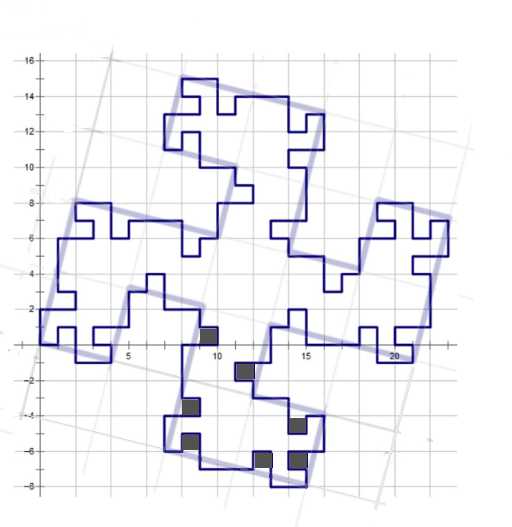
数一下就会发现4个拐中的每个拐都缺了7块

就这样 神奇的7和17都得到了。。。

然后解啊解啊就能解出那个鬼畜的公式了。

有了公式这题就很简单了

只需要用ex_gcd求出5的逆元，然后套一套公式，模一模就完成了~

代码：

 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <climits>
 #include <cctype>
 #include <cmath>
 #include <string>
 #include <sstream>
 #include <iostream>
 #include <algorithm>
 #include <iomanip>
 using namespace std;
 #include <queue>
 #include <stack>
 #include <vector>
 #include <deque>
 #include <set>
 #include <map>
 typedef long long LL;
 typedef long double LD;
 const double pi=acos(-1.0);
 const double eps=1e-;
 #define INF 0x3f3f3f
 #define lson l, m, rt<<1
 #define rson m+1, r, rt<<1|1
 typedef pair<int, int> PI;
 typedef pair<int, PI > PP;
 #ifdef _WIN32
 #define LLD "%I64d"
 #else
 #define LLD "%lld"
 #endif
 //#pragma comment(linker, "/STACK:1024000000,1024000000")
 //LL quick(LL a, LL b){LL ans=1;while(b){if(b & 1)ans*=a;a=a*a;b>>=1;}return ans;}
 //inline int read(){char ch=' ';int ans=0;while(ch<'0' || ch>'9')ch=getchar();while(ch<='9' && ch>='0'){ans=ans*10+ch-'0';ch=getchar();}return ans;}
 inline void print(LL x){printf(LLD, x);puts("");}
 //inline void read(LL &ret){char c;int sgn;LL bit=0.1;if(c=getchar(),c==EOF) return ;while(c!='-'&&c!='.'&&(c<'0'||c>'9')) c=getchar();sgn=(c=='-')?-1:1;ret=(c=='-')?0:(c-'0');while(c=getchar(),c>='0'&&c<='9') ret=ret*10+(c-'0');if(c==' '||c=='\n'){ ret*=sgn; return ; }while(c=getchar(),c>='0'&&c<='9') ret+=(c-'0')*bit,bit/=10;ret*=sgn;}
 const int mod=;

 LL quick(LL a, LL b)
 {
     LL ans=;
     while(b)
     {
         if(b & )ans=(ans*a)%mod;
         a=(a*a)%mod;
         b>>=;
     }
     return ans%mod;
 }

 void ex_gcd(int a, int b, int &x, int &y)
 {
     if(b)
     {
         ex_gcd(b, a%b, x, y);
         int tmp=x;
         x=y;
         y=tmp-(a/b)*y;
     }
     else
     {
         x=, y=;
         return ;
     }
 }
 int main()
 {
     int t;
     scanf("%d", &t);
     while(t--)
     {
         int n;
         scanf("%d", &n);
         if(n==)
         {
             printf("1\n");
             continue;
         }
         int x, y;
         ex_gcd(, mod, x, y);
         print((((*quick(, n))%mod+(*quick(, n))%mod)*x)%mod);
     }
     return ;
 }

CSUOJ 1413