20169210《Linux内核原理与分析》第二周作业

《Linux内核原理与分析》第二周作业

本周作业分为两部分：第一部分为观看学习视频并完成实验楼实验一；第二部分为看《Linux内核设计与实现》1、2、18章并安装配置内核。

---

第一部分

本部分主要是观看孟老师的学习视频，学习计算机是如何工作的，并根据提示完成实验。

寄存器

通用寄存器:

• AX：累加器
• BX：基地址寄存器
• CX：计数寄存器
• DX：数据寄存器
• BP：堆栈基址针
• SI、DI：变址寄存器
• SP：堆栈顶指针

段寄存器:

• CS：代码段寄存器，指向包含程序指令的段。
• SS：栈段寄存器，指向包含当前程序栈的段。
• DS：数据段寄存器，指向包含静态数据或者全局数据段。
• ES：附加寄存器，指向附加数据段。

寻址方式

• movl %eax，%edx edx=eax 寄存器寻址
• movl $0x123，%edx edx=0x123 立即寻址
• movl 0x123，%edx edx=*（int32_t）0x123 直接寻址
• movl （%ebx），%edx edx=（int32_t）ebx 间接寻址
• movl 4（%ebx），%edx edx=（int32_t）(ebx+4) 变址寻址

b、w、l、q分别代表8位、16位、32位和64位。

实验

实验一为反汇编一段c语言代码。

首先用如下命令输入一段C语言代码

$vi main.c

然后用如下命令反汇编

$gcc -S -o main.s main.c -m32

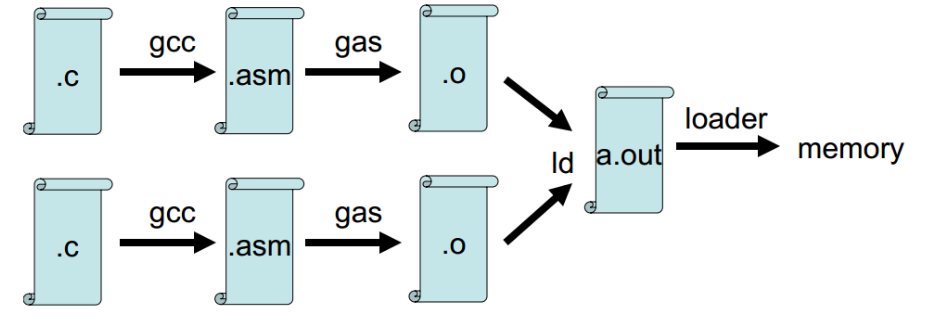
其中gcc命令及其相关命令如下图所示

用如下命令查看汇编代码

$vi main.s

前面带“ . ”的语句是用于链接辅助信息的，并不会执行，所以要去掉，结果如下

g:
	pushl	%ebp
	movl	%esp, %ebp
	movl	8(%ebp), %eax
	addl	$3, %eax
	popl	%ebp
	ret
f:
	pushl	%ebp
	movl	%esp, %ebp
	subl	$4, %esp
	movl	8(%ebp), %eax
	movl	%eax, (%esp)
	call	g
	leave
	ret
main:
	pushl	%ebp
	movl	%esp, %ebp
	subl	$4, %esp
	movl	$8, (%esp)
	call	f
	addl	$1, %eax
	leave
	ret

具体的堆栈分析如下图所示

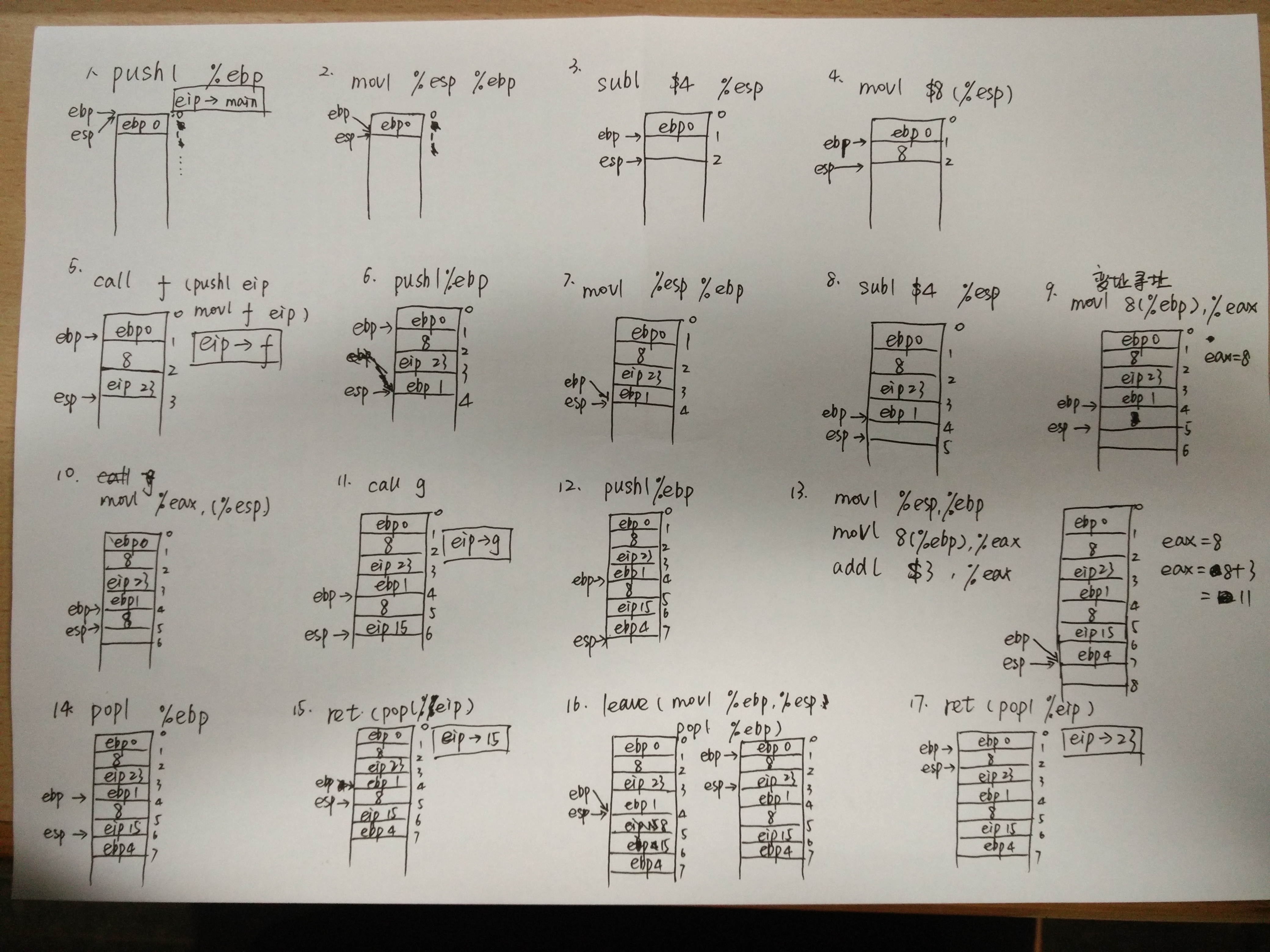
其中

pushl   %ebp

表示压栈

popl   %ebp

表示出栈

第二部分

本部分为阅读《Linux内核设计与实现》并安装好Linux内核。

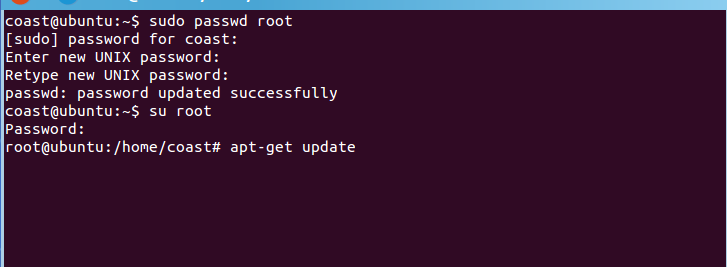
首先用如下命令设置好root密码，并进入root用户。

$sudo passwd root
$su root

如图所示

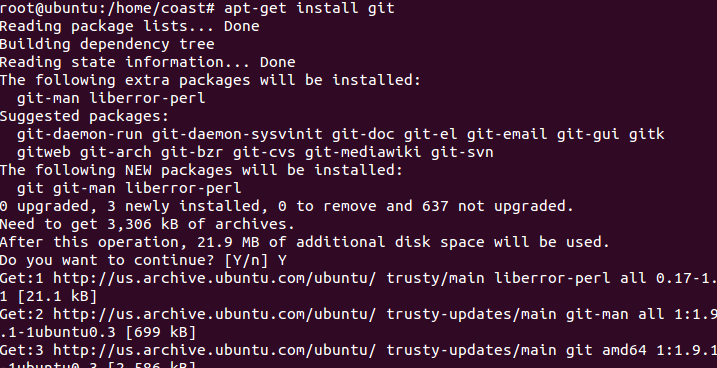
接下来是安装git并下载安装包,命令如下

$apt-get update
$apt-get install git

如下图所示

由于下载的是linux-4.7.6.tar.xz，所以需要解压，命令如下

$cd Downloads
$tar -xvf linux-4.7.6.tar.xz

如下图所示

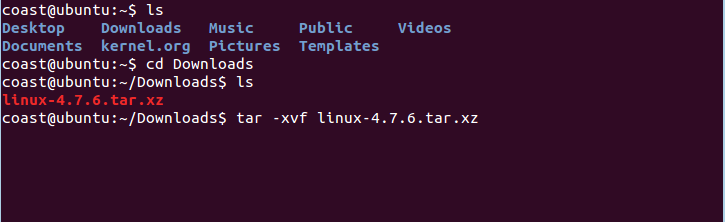
解压完成后进行配置，使用以下命令

$cd linux-4.7.6
$make menuconfig

结果如下

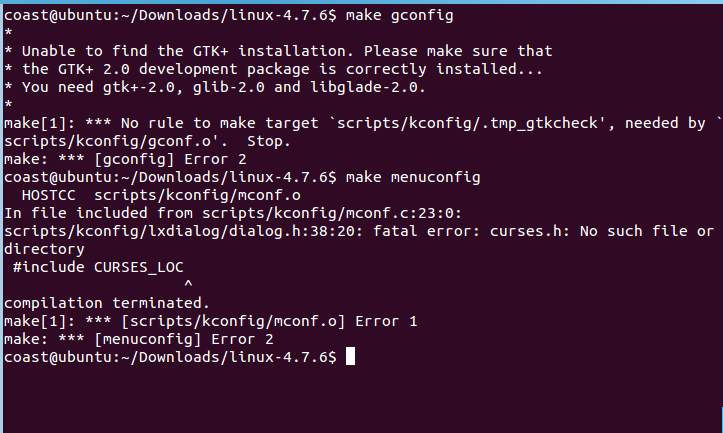
在配置时遇到了问题，暂时不知道什么原因，也不知道解决办法，等日后找到解决办法再更新。