题目仿佛在讽刺我。。。

第一题：

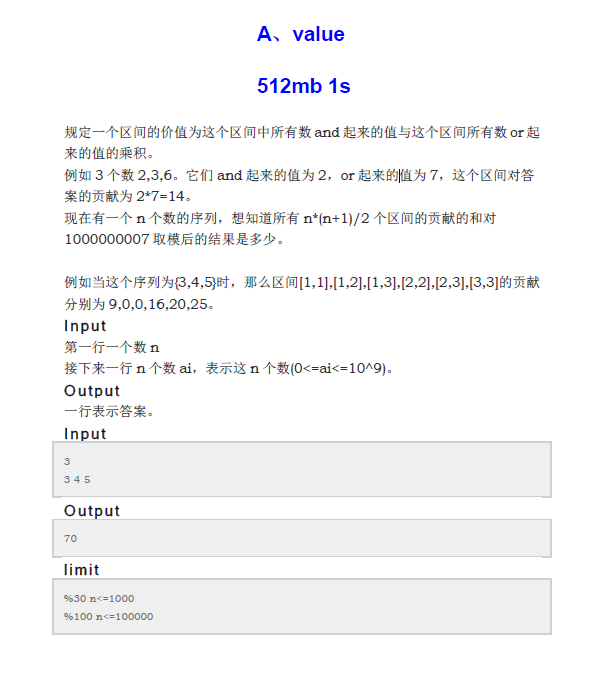
题解：

考虑枚举区间右端点，维护所以左到当前的 and 和 or 。注意 and 每次变化至少有一个二进制位从1变 0，or 每次至少有一个位从0变 1，所以最多有log段不同的值。用两个链表维护这log个值，暴力计算答案即可。
O( nlogn)

我原本打的是一个树状数组的O（nlognlogn）算法。。然后被卡了。。只有50分。。

看了看奥爷爷的代码，发现他直接用一个链表同时维护and和or值，真奇怪啊不是(logn)^2吗。。然后男神说这个也是log级别的，因为两个区间不同只能是边界上跨越。

代码：

  1.  #include<cstdio>
  2.  #include<cstdlib>
  3.  #include<cstring>
  4.  #include<iostream>
  5.  #include<algorithm>
  6.  using namespace std;
  7.  
  8.  typedef long long LL;
  9.  const int N=;
  10.  const LL mod=;
  11.  int n,al;
  12.  struct node{int last,next;LL t0,t1,sum;}a[N];
  13.  
  14.  int main()
  15.  {
  16.      // freopen("a.in","r",stdin);
  17.      // freopen("a.out","w",stdout);
  18.      freopen("value.in","r",stdin);
  19.      freopen("value.out","w",stdout);
  20.      scanf("%d",&n);
  21.      al=;
  22.      int x,last=;
  23.      LL ans=;
  24.      for(int i=;i<=n;i++)
  25.      {
  26.          scanf("%d",&x);
  27.          for(int j=last;j;j=a[j].last)
  28.          {
  29.              a[j].t0&=x;
  30.              a[j].t1|=x;
  31.          }
  32.          a[++al].t0=x;a[al].t1=x;a[al].sum=;
  33.          a[al].last=last;
  34.          if(last) a[last].next=al;
  35.          last=al;
  36.  
  37.          for(int j=last;j;j=a[j].last)
  38.          {
  39.              int p=a[j].last;
  40.              if(p && a[p].t0==a[j].t0 && a[p].t1==a[j].t1)
  41.              {
  42.                  a[p].sum+=a[j].sum;
  43.                  a[p].next=a[j].next;
  44.                  if(a[j].next) a[a[j].next].last=p;
  45.                  else last=p;//debug last=p not last=j
  46.              }
  47.          }
  48.  
  49.          for(int j=last;j;j=a[j].last)
  50.          {
  51.              ans=(ans+((((a[j].t0*a[j].t1)%mod)*a[j].sum)%mod))%mod;
  52.          }
  53.      }
  54.      printf("%I64d\n",ans);
  55.      return ;
  56.  }

第二题 bzoj3652

3652: 大新闻

Time Limit: 10 Sec  Memory Limit: 512 MBSec  Special Judge
Submit: 207  Solved: 106
[Submit][Status][Discuss]

Description

Input 两个整数n和p。p/100表示题目中描述的概率

Output 输出期望在模1000000007下的值


Sample Input

3 50

Sample Output

2

HINT

1<=N<=10^18

 
题解：
这题的数位dp达到我都昏了。。因为我打得挺复杂的。。
首先贴一个我的代码吧。
  1.  #include<cstdio>
  2.  #include<cstdlib>
  3.  #include<cstring>
  4.  #include<iostream>
  5.  #include<algorithm>
  6.  using namespace std;
  7.  
  8.  typedef long long LL;
  9.  const LL mod=;
  10.  const int N=;
  11.  LL n,m,p,bit[N],vis[N][][],cnt[N][],f[N][][][][],g[N][][];
  12.  int d[N];
  13.  
  14.  LL ad(LL x,LL y){return ((x+y)%mod+mod)%mod;}
  15.  
  16.  int find_vis(int x,int now,int flag)
  17.  {
  18.      if(x==) return ;
  19.      if(vis[x][now][flag]!=-) return vis[x][now][flag];
  20.      int mx=;if(flag || (x-==)) mx=d[x-];
  21.      LL ans=;
  22.      for(int i=;i<=mx;i++)
  23.      {
  24.          ans=ad(ans,find_vis(x-,i,flag&(i==d[x-])));
  25.      }
  26.      vis[x][now][flag]=ans;
  27.      // printf("x = %d  now = %d  flag = %d  = %d\n",x,now,flag,ans);
  28.      return ans;
  29.  }
  30.  
  31.  void find_cnt()
  32.  {
  33.      for(int i=;i<=m;i++) cnt[i][]=cnt[i][]=bit[m];
  34.      for(int i=m;i>=;i--)
  35.      {
  36.          if(d[i]==)
  37.          {
  38.              for(int j=i-;j>=;j--)
  39.              {
  40.                  cnt[j][]=ad(cnt[j][],-bit[i-]);
  41.                  cnt[j][]=ad(cnt[j][],-bit[i-]);
  42.              }
  43.              cnt[i][]=ad(cnt[i][],-bit[i]);
  44.              for(int j=i+;j<=m;j++)
  45.              {
  46.                  cnt[j][d[j]]=ad(cnt[j][d[j]],-bit[i]);
  47.              }
  48.          }
  49.      }
  50.  
  51.  }
  52.  
  53.  int dfs(int x,int now1,int now2,int flag1,int flag2)
  54.  {
  55.      if(x==) return ;
  56.  
  57.      if(f[x][now1][now2][flag1][flag2]!=-) return f[x][now1][now2][flag1][flag2];
  58.      LL ans=,now=;
  59.      int mx1=;if(flag1 || (x-==)) mx1=d[x-];
  60.      int mx2=;if(flag2 || (x-==)) mx2=d[x-];
  61.      if(now1+now2==) ans=ad(ans,(vis[x][now1][flag1]*bit[x])%mod);
  62.      for(int i=;i<=mx1;i++)
  63.      {
  64.          if(flag2 && (i^)>mx2)
  65.          {
  66.              int f1=flag1&(i==d[x-]);
  67.              int f2=flag2&(==d[x-]);
  68.              ans=ad(ans,dfs(x-,i,,f1,f2));
  69.          }
  70.          else
  71.          {
  72.              int f1=flag1&(i==d[x-]);
  73.              int f2=flag2&((i^)==d[x-]);
  74.              ans=ad(ans,dfs(x-,i,i^,f1,f2));
  75.          }
  76.      }
  77.      f[x][now1][now2][flag1][flag2]=ans;
  78.      // printf("f x = %d  now1 = %d  now2 = %d  flag1 = %d  flag2 = %d  ans = %d\n",x,now1,now2,flag1,flag2,ans);
  79.      return ans;
  80.  }
  81.  
  82.  int DFS(int x,int now,int flag)
  83.  {
  84.      if(x==) return ;
  85.      if(g[x][now][flag]!=-) return g[x][now][flag];
  86.      int mx=;if(flag || (x-==)) mx=d[x-];
  87.      LL ans=;
  88.      ans=ad(ans,(((vis[x][now][flag]*cnt[x][now^])%mod)*bit[x])%mod);
  89.      for(int i=;i<=mx;i++)
  90.      {
  91.          ans=ad(ans,DFS(x-,i,flag&(i==d[x-])));
  92.      }
  93.      g[x][now][flag]=ans;
  94.      // printf("g x = %d  now = %d  flag = %d  = %d\n",x,now,flag,ans);
  95.      return ans;
  96.  }
  97.  
  98.  LL quickpow(LL x,LL y)
  99.  {
  100.      LL ans=;
  101.      while(y)
  102.      {
  103.          if(y&) ans=(ans*x)%mod;
  104.          x=(x*x)%mod;
  105.          y/=;
  106.      }
  107.      return ans;
  108.  }
  109.  
  110.  int main()
  111.  {
  112.      freopen("a.in","r",stdin);
  113.      // freopen("a.out","w",stdout);
  114.      // freopen("news.in","r",stdin);
  115.      // freopen("news.out","w",stdout);
  116.      scanf("%lld%lld",&n,&p);
  117.      LL x=n-;m=;
  118.      memset(d,,sizeof(d));
  119.      while(x)
  120.      {
  121.          d[++m]=x%;
  122.          x/=;
  123.      }
  124.      bit[]=;
  125.      for(int i=;i<=;i++) bit[i]=(bit[i-]*)%mod;
  126.      memset(cnt,,sizeof(cnt));
  127.      memset(vis,-,sizeof(vis));
  128.      memset(f,-,sizeof(f));
  129.      memset(g,-,sizeof(g));
  130.      find_vis(m+,,);
  131.      find_cnt();
  132.  
  133.      LL a1=dfs(m+,,,,);
  134.      LL a2=DFS(m+,,);
  135.      LL bn=quickpow(n%mod,mod-);
  136.      LL bb=quickpow(,mod-);
  137.      LL ans=;
  138.  
  139.      // for(int i=1;i<=3;i++)
  140.          // for(int j=0;j<=1;j++)
  141.              // printf("cnt %d %d = %I64d\n",i,j,cnt[i][j]);
  142.  
  143.      ans=ad(ans,(((a1*bn)%mod)*((p*bb)%mod))%mod);
  144.      ans=ad(ans,(((((a2*bn)%mod)*bn)%mod)*(((-p)*bb)%mod))%mod);
  145.      // printf("a1=%I64d a2=%I64d\n",a1,a2);
  146.      printf("%lld\n",ans);
  147.      return ;
  148.  }

x表示当前填到哪一位。flag表示当前是否和边界重合。

dfs是做加密的情况，也就是确定当前填的x，然后让跟它异或的y尽量大。

DFS是做不加密的情况，也就是确定当前填的x，然后y所有可能都算上。

其中vis是维护到当前状态的方案数。

cnt是表示当前某个数位上是0或1的方案数。

好了还是这种做法太复杂了。。

学习了一下出题人的做法。

出题人题解：

  1.  #include<cstdio>
  2.  #include<cstdlib>
  3.  #include<cstring>
  4.  #include<cmath>
  5.  #include<iostream>
  6.  #include<algorithm>
  7.  using namespace std;
  8.  
  9.  typedef long long LL;
  10.  const LL mod=;
  11.  const int N=;
  12.  LL n,m,p,bit[N],f[N][][],g[N][][];
  13.  int a[N];
  14.  
  15.  LL quickpow(LL x,LL y)
  16.  {
  17.      LL ans=;
  18.      while(y)
  19.      {
  20.          if(y&) ans=(ans*x)%mod;
  21.          x=(x*x)%mod;
  22.          y/=;
  23.      }
  24.      return ans;
  25.  }
  26.  
  27.  void dp_1()
  28.  {
  29.      memset(f,,sizeof(f));
  30.      memset(g,,sizeof(g));
  31.      g[][][]=;
  32.      int now1,now2;
  33.      for(int i=;i<m;i++)
  34.          for(int x1=;x1<=;x1++)
  35.              for(int x2=;x2<=;x2++)
  36.              {
  37.                  if(g[i][x1][x2]==) continue;
  38.                  for(int j=;j<=;j++)
  39.                  {
  40.                      int k=j^;
  41.                      if(j>a[i+] && x1) continue;
  42.                      if(j==a[i+] && x1) now1=;
  43.                      else now1=;
  44.                      if(k>a[i+] && x2) k=;
  45.                      if(k==a[i+] && x2) now2=;
  46.                      else now2=;
  47.                      g[i+][now1][now2]=(g[i+][now1][now2]+g[i][x1][x2])%mod;
  48.                      f[i+][now1][now2]=(f[i+][now1][now2]+f[i][x1][x2]+((g[i][x1][x2]*(j^k))%mod*bit[i+])%mod)%mod;
  49.                  }
  50.              }
  51.  }
  52.  
  53.  void dp_2()
  54.  {
  55.      memset(f,,sizeof(f));
  56.      memset(g,,sizeof(g));
  57.      g[][][]=;
  58.      int now1,now2;
  59.      for(int i=;i<m;i++)
  60.          for(int x1=;x1<=;x1++)
  61.              for(int x2=;x2<=;x2++)
  62.              {
  63.                  if(g[i][x1][x2]==) continue;
  64.                  for(int j=;j<=;j++)
  65.                  {
  66.                      if(j>a[i+] && x1) continue;
  67.                      if(x1 && j==a[i+]) now1=;
  68.                      else now1=;
  69.                      for(int k=;k<=;k++)
  70.                      {
  71.                          if(k>a[i+] && x2) continue;
  72.                          if(x2 && k==a[i+]) now2=;
  73.                          else now2=;
  74.                          g[i+][now1][now2]=(g[i+][now1][now2]+g[i][x1][x2])%mod;
  75.                          f[i+][now1][now2]=(f[i+][now1][now2]+f[i][x1][x2]+(g[i][x1][x2]*(j^k))%mod*bit[i+]%mod)%mod;
  76.                      }
  77.                  }
  78.              }
  79.  }
  80.  
  81.  int main()
  82.  {
  83.      freopen("a.in","r",stdin);
  84.      // freopen("news.in","r",stdin);
  85.      // freopen("news.out","w",stdout);
  86.      scanf("%lld%lld",&n,&p);
  87.      LL x=n-,a1=,a2=;m=;
  88.      while(x)
  89.      {
  90.          a[++m]=x%;
  91.          x/=;
  92.      }
  93.      for(int i=;i<=m/;i++) swap(a[i],a[m-i+]);
  94.      bit[m]=;
  95.      for(int i=m-;i>=;i--) bit[i]=(bit[i+]*)%mod;
  96.      // for(int i=1;i<=m;i++) printf("%d ",a[i]);printf("\n");
  97.  
  98.      dp_1();
  99.      for(int i=;i<=;i++)
  100.          for(int j=;j<=;j++)
  101.              a1=(a1+f[m][i][j])%mod;
  102.      dp_2();
  103.      for(int i=;i<=;i++)
  104.          for(int j=;j<=;j++)
  105.              a2=(a2+f[m][i][j])%mod;
  106.  
  107.      LL bn=quickpow(n%mod,mod-);
  108.      LL bb=quickpow(,mod-);
  109.      LL ans=;
  110.  
  111.      ans=(ans+((a1*bn%mod)*(p*bb%mod))%mod)%mod;
  112.      ans=(ans+((((a2*bn%mod)*bn)%mod)*((-p)*bb%mod))%mod)%mod;
  113.      // printf("a1=%I64d a2=%I64d\n",a1,a2);
  114.      printf("%lld\n",ans);
  115.  
  116.      return ;
  117.  }

第三题：

3653: 谈笑风生

Time Limit: 20 Sec  Memory Limit: 512 MB
Submit: 689  Solved: 264
[Submit][Status][Discuss]

Description

设T 为一棵有根树，我们做如下的定义：
• 设a和b为T 中的两个不同节点。如果a是b的祖先，那么称“a比b不知道
高明到哪里去了”。
• 设a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定
常数x，那么称“a 与b 谈笑风生”。
给定一棵n个节点的有根树T，节点的编号为1 到 n，根节点为1号节点。你需
要回答q 个询问，询问给定两个整数p和k，问有多少个有序三元组(a;b;c)满足：
1. a、b和 c为 T 中三个不同的点，且 a为p 号节点；
2. a和b 都比 c不知道高明到哪里去了；
3. a和b 谈笑风生。这里谈笑风生中的常数为给定的 k。

Input

输入文件的第一行含有两个正整数n和q，分别代表有根树的点数与询问的个数。接下来n - 1行，每行描述一条树上的边。每行含有两个整数u和v，代表在节点u和v之间有一条边。
接下来q行，每行描述一个操作。第i行含有两个整数，分别表示第i个询问的p和k。

Output

输出 q 行，每行对应一个询问，代表询问的答案。

Sample Input

5 3
1 2
1 3
2 4
4 5
2 2
4 1
2 3

Sample Output

3
1
3

HINT

1<=P<=N

1<=K<=N

N<=300000

Q<=300000

 
题解：
 
跟我最近做的主席树模版题非常像啊。。
  1.  #include<cstdio>
  2.  #include<cstdlib>
  3.  #include<cstring>
  4.  #include<iostream>
  5.  #include<algorithm>
  6.  using namespace std;
  7.  
  8.  typedef long long LL;
  9.  const int N=*,M=*;
  10.  // const int N=2*300000,M=30*300000;
  11.  struct node{
  12.      int x,y,next;
  13.  }a[N];
  14.  struct trnode{
  15.      int lc,rc;
  16.      LL sum;
  17.  }t[M];
  18.  int n,m,num,len,tl;
  19.  int first[N],dfn[N],edfn[N],dep[N],tot[N],root[N];
  20.  
  21.  int minn(int x,int y){return x<y ? x:y;}
  22.  
  23.  void ins(int x,int y)
  24.  {
  25.      a[++len].x=x;a[len].y=y;
  26.      a[len].next=first[x];first[x]=len;
  27.  }
  28.  
  29.  int add(int rt,int x,int d)
  30.  {
  31.      int now=++tl,tmp=now;
  32.      int l=,r=n,mid;
  33.      while(l<r)
  34.      {
  35.          mid=(l+r)/;
  36.          if(x<=mid)
  37.          {
  38.              r=mid;
  39.              t[now].lc=++tl;
  40.              t[tl].lc=t[tl].rc=;
  41.              t[now].rc=t[rt].rc;
  42.              rt=t[rt].lc;
  43.              now=tl;
  44.          }
  45.          else
  46.          {
  47.              l=mid+;
  48.              t[now].lc=t[rt].lc;
  49.              t[now].rc=++tl;
  50.              t[tl].lc=t[tl].rc=;
  51.              rt=t[rt].rc;
  52.              now=tl;
  53.          }
  54.          t[now].sum=t[rt].sum+d;
  55.      }
  56.      return tmp;
  57.  }
  58.  
  59.  LL query(int lx,int rx,int ql,int qr,int l,int r)
  60.  {
  61.      if(ql==l && qr==r) return t[rx].sum-t[lx].sum;//debug 一开始更新到了叶子节点。。
  62.      int mid=(l+r)/;
  63.      if(qr<=mid) return query(t[lx].lc,t[rx].lc,ql,qr,l,mid);
  64.      if(ql>mid) return query(t[lx].rc,t[rx].rc,ql,qr,mid+,r);
  65.      return query(t[lx].lc,t[rx].lc,ql,mid,l,mid)+query(t[lx].rc,t[rx].rc,mid+,qr,mid+,r);
  66.  }
  67.  
  68.  void dfs(int x,int fa)
  69.  {
  70.      dep[x]=dep[fa]+;
  71.      dfn[x]=++num;
  72.      tot[x]=;
  73.      for(int i=first[x];i;i=a[i].next)
  74.      {
  75.          int y=a[i].y;
  76.          if(y==fa) continue;
  77.          dfs(y,x);
  78.          tot[x]+=tot[y];
  79.      }
  80.      edfn[x]=num;
  81.  }
  82.  
  83.  void build_tree(int x,int fa)
  84.  {
  85.      root[dfn[x]]=add(root[dfn[x]-],dep[x],tot[x]-);
  86.      for(int i=first[x];i;i=a[i].next)
  87.      {
  88.          int y=a[i].y;
  89.          if(y==fa) continue;
  90.          build_tree(y,x);
  91.      }
  92.  }
  93.  
  94.  void output(int x,int l,int r)
  95.  {
  96.      printf("x = %d l = %d  r = %d  lc = %d  rc = %d  sum = %d\n",x,l,r,t[x].lc,t[x].rc,t[x].sum);
  97.      int mid=(l+r)/;
  98.      if(t[x].lc) output(t[x].lc,l,mid);
  99.      if(t[x].rc) output(t[x].rc,mid+,r);
  100.  }
  101.  
  102.  int main()
  103.  {
  104.      // freopen("a.in","r",stdin);
  105.      freopen("tree.in","r",stdin);
  106.      freopen("tree.out","w",stdout);
  107.      scanf("%d%d",&n,&m);
  108.      num=;tl=;len=;
  109.      memset(first,,sizeof(first));
  110.      for(int i=;i<n;i++)
  111.      {
  112.          int x,y;
  113.          scanf("%d%d",&x,&y);
  114.          ins(x,y);
  115.          ins(y,x);
  116.      }
  117.      dfs(,);
  118.      root[]=;t[].lc=t[].rc=;
  119.      build_tree(,);
  120.      LL ans;int p,k;
  121.      for(int i=;i<=m;i++)
  122.      {
  123.          scanf("%d%d",&p,&k);
  124.          ans=((LL)minn(dep[p]-,k))*((LL)(tot[p]-));
  125.          ans+=query(root[dfn[p]],root[edfn[p]],minn(n,dep[p]+),minn(n,dep[p]+k),,n);
  126.          printf("%lld\n",ans);
  127.      }
  128.      return ;
  129.  }

【20151105noip膜你赛】bzoj3652 bzoj3653的更多相关文章

  1. cdcqの省选膜你赛

    cdcqの省选膜你赛 比赛当天因为在杠hnoi2016的大数据结构没有参加,今天补了一下.挺好玩的虽然不看一句话题意的话真的卡读题 此生无悔入东方,来世愿生幻想乡 2651. 新史「新幻想史 -现代史 ...

  2. 【良心noip膜你赛】总结

    一点都不良心!!!! AK 快乐爆零快乐!!! 1. A. value512mb 1s规定一个区间的价值为这个区间中所有数 and 起来的值与这个区间所有数 or 起来的值的乘积.例如 3 个数 2, ...

  3. 2016-5-19模拟测试 bzoj3652 bzoj3653 bzoj3654

    T1 description 给定正整数\(n\),定义\(f(x) = \max{y \ \mathrm{xor}\ x}(y<n)\) \(x\)在\([0,n)\)随机取值,求\(f(x) ...

  4. EZ 2018 1 21 2018noip第五次膜你赛

    这次分数普遍偏高,而且yu'ben'ao又AK了! 但是最后一题莫名爆0让我很感伤啊(搓了1个多小时的20分暴力)! 难度偏低,主要是T2没剪枝,炸了3个点. T1 这种SB题恐怕是千年难遇了,PJ- ...

  5. EZ 2018 01 14 2018noip第四次膜你赛

    这次惨烈的炸了个精光(只有20),然后对我的OI想法造成了巨大的转折. (以上有点作,其实我只是再也不用vector存图了而已(用邻接表)) 难度很不均匀,而且题型很狗(还有结论题???) T1 坑人 ...

  6. EZ 2017 12 30 2018noip第二次膜你赛

    去年的比赛了,然而今天才改好. 总体难度适中,有大佬AK. 主要是自己SB第二题没想出来,然后又是可怜的100来分. T1 一道二分+数学的题目. 我们可以二分叫的次数,然后用公式(等差数列,公差都是 ...

  7. EZ 2017 12 17初二初三第一次膜你赛

    以后平时练习还是写一写吧. (题目搞来搞去太烦了,直接PDF存起来) T1 水题(???),主要是数据水,正解是设一个阙值,然而根本没人打.(暴力出奇迹) CODE #include<cstdi ...

  8. [SinGuLaRiTy] NOIP 膜你赛-Day 2

    [SinGuLaRiTy-1031] Copyright (c) SinGuLaRiTy 2017. All Rights Reserved. 对于所有题目: Time Limit: 1s | Mem ...

  9. [SinGuLaRiTy] NOIP膜你赛-Day 1

    [SinGuLRiTy-1022] Copyright (c) SinGuLaRITy 2017. All Rights Reserved.  对于所有题目:Time Limit:1s || Memo ...

随机推荐

  1. oracle数据库之游标的使用

    一.游标概念 为了处理 SQL 语句,ORACLE 必须分配一片叫上下文( context area )的区域来处理所必需的信息,其中包括要处理的行的数目,一个指向语句被分析以后的表示形式的指针以及查 ...

  2. AWVS使用基础教程

    什么是AWVS Acunetix Web Vulnerability Scanner(简称AWVS)是一款知名的网络漏洞扫描工具,它通过网络爬虫测试你的网站安全,检测流行安全漏洞,现已更新到10.(下 ...

  3. deep learning3

    9.3.Restricted Boltzmann Machine (RBM)受限玻尔兹曼基 假设有一个二部图,每一层的节点之间没有链接,一层是可视层,即输入数据层(v),一层是隐藏层(h),如果假设所 ...

  4. HUAS 1483 mex(莫队算法)

    考虑莫队算法,对于区间减小的情况,可以O(1)解决.对于区间增加的情况,可能需要O(n)解决.好在数据不卡莫队. 1200ms过了. 离线+线段树 760ms过了. # include <cst ...

  5. vijos1859[TJOI2014]电源插排

    题意:小 M 的实验室有很多电源插排.这些插排的编号从 1 到 N,由左向右排成一排.每天早晨,这些插排都是没有被使用的.每当一个学生来到实验室,他就将自己的笔记本电源插到某一个未被使用的插排上.实验 ...

  6. 【bzoj4579】[Usaco2016 Open]Closing the Farm 并查集

    题目描述 Farmer John and his cows are planning to leave town for a long vacation, and so FJ wants to tem ...

  7. 【bzoj4698】[Sdoi2008] Sandy的卡片 后缀数组

    题目描述 Sandy和Sue的热衷于收集干脆面中的卡片.然而,Sue收集卡片是因为卡片上漂亮的人物形象,而Sandy则是为了积攒卡片兑换超炫的人物模型.每一张卡片都由一些数字进行标记,第i张卡片的序列 ...

  8. Codeforces Round#516 Div.1 翻车记

    A:开场懵逼.然后发现有人1min过,于是就sort了一下,于是就过了.正经证明的话,考虑回文串两端点一定是相同的,所以最多有Σcnti*(cnti+1)/2个,cnti为第i种字母出现次数.而sor ...

  9. Give NetScaler a “Tune-Up”

    Give NetScaler a “Tune-Up” https://www.citrix.com/blogs/2014/10/21/give-netscaler-a-tune-up/ To Opti ...

  10. Android Bitmap和Drawable互转及使用BitmapFactory解析图片流

    一.Bitmap转Drawable Bitmap bmp=xxx; BitmapDrawable bd=new BitmapDrawable(bmp); 因为BtimapDrawable是Drawab ...