最短路-Bellmanford

简介：

给定一个图和一个源点，求源点到其余点的最短路径，图中有可能存在负权边。

算法步骤

1.初始化：将除源点外的所有顶点的最短距离估计值 dist[v] ← +∞, dist[s] ←0; 
2.迭代求解：反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离；（运行|v|-1次） 
3.检验负权回路：判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解；否则算法返回true，并且从源点可达的顶点v的最短距离保存在 dist[v]中。

如果存在从源点可达的权为负的回路。则 应为无法收敛而导致不能求出最短路径。

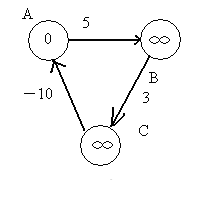
经过第一次遍历后，点B的值变为5，点C的值变为8，这时，注意权重为－10的边，这条边的存在，导致点A的值变为－2。（8＋ －10＝－2）

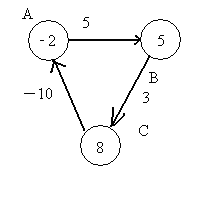
第二次遍历后，点B的值变为3，点C变为6，点A变为－4。正是因为有一条负边在回路中，导致每次遍历后，各个点的值不断变小。所以这是无限循环的。

#include<iostream>
#include<cstdio>
using namespace std;
#define MAX 0x3f3f3f3f
#define N 1010
int nodenum, edgenum, original; //点，边，起点
typedef struct Edge //边
{
    int u, v;
    int cost;
} Edge;
Edge edge[N];
int dis[N], pre[N];
bool Bellman_Ford()
{
    int ok;
    ; i <= nodenum; ++i) //初始化，起点本身赋值为0，其余赋值为最大
        dis[i] = (i == original ?  : MAX);
    ; i <= nodenum - ; ++i)
    {
        ok=;
        ; j <= edgenum; ++j)
            if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛（顺序一定不能反）
            {
                dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
                pre[edge[j].v] = edge[j].u;//这里用来存储路径
                ok=;
            }
        ) //优化这里，如果这趟没跟新任何节点就可以直接退出了。
            break;
    }
    ; //判断是否含有负权回路
    ; i <= edgenum; ++i)
        if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
        {
            flag = ;
            break;
        }
    return flag;
}
void print_path(int root) //打印最短路的路径（反向）
{
    while(root != pre[root]) //前驱
    {
        printf("%d-->", root);
        root = pre[root];
    }
    if(root == pre[root])
        printf("%d\n", root);
}

int main()
{
    scanf("%d%d%d", &nodenum, &edgenum, &original);//输入点边起点，一般起点规定为1
    pre[original] = original;//为了输出最短路用的，前驱为本身
    ; i <= edgenum; ++i)
    {
        scanf("%d%d%d", &edge[i].u, &edge[i].v, &edge[i].cost);//有向图
    }
    if(Bellman_Ford())//如果没有负权
        ; i <= nodenum; ++i) //每个点最短路
        {
            printf("%d\n", dis[i]);
            printf("Path:");
            print_path(i);
        }
    else
        printf("have negative circle\n");
    ;
}