【matlab】MTATLAB解线性方程组
在求解线性方程组时,会遇到以下几种情形:定解方程组、不定方程组、超定方程组、奇异方程组。
首先以定解线性方程组为例:
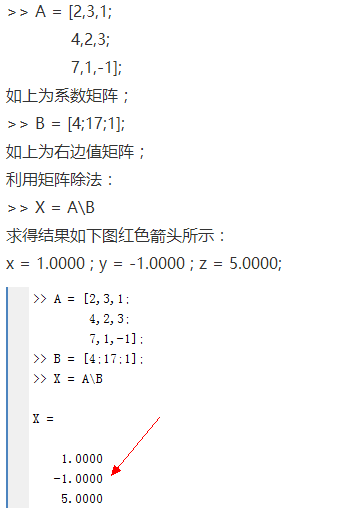
format rat 化成分数
format short
>> A=[,;,] A = >> B=[;] B = >> X=A\B X = 34.4828
12.4138 >> format rat
>> X X = /
/ >> /*+/* ans = / >>
>> format long
>> ans ans = 3.903448275862069e+02 >> format short
>> ans ans = 390.3448
【matlab】MTATLAB解线性方程组的更多相关文章
- matlab中求解线性方程组的rref函数
摘自:http://www.maybe520.net/blog/987/ matlab中怎么求解线性方程组呢? matlab中求解线性方程组可应用克拉默法则(Cramer's Rule)即通过det( ...
- 高斯消去法解线性方程组(MPI)
用一上午的时间,用MPI编写了高斯消去法解线性方程组.这次只是针对单线程负责一个线程方程的求解,对于超大规模的方程组,需要按行分块,后面会在这个基础上进行修改.总结一下这次遇到的问题: (1)MPI_ ...
- MATLAB矩阵的LU分解及在解线性方程组中的应用
作者:凯鲁嘎吉 - 博客园http://www.cnblogs.com/kailugaji/ 三.实验程序 五.解答(按如下顺序提交电子版) 1.(程序) (1)LU分解源程序: function [ ...
- Eigen解线性方程组
一. 矩阵分解: 矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积,可分为三角分解.满秩分解.QR分解.Jordan分解和SVD(奇异值)分解等,常见 ...
- 《Fluid Engine Development》 学习笔记1-求解线性方程组
我个人对基于物理的动画很感兴趣,最近在尝试阅读<Fluid Engine Development>,由于内容涉及太多的数学问题,而单纯学习数学又过于枯燥,难以坚持学习(我中途放弃好多次了) ...
- Widget Factory (高斯消元解线性方程组)
The widget factory produces several different kinds of widgets. Each widget is carefully built by a ...
- 计算方法 -- 解线性方程组直接法(LU分解、列主元高斯消元、追赶法)
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> ...
- 题解【AcWing883】高斯消元解线性方程组
题面 高斯消元模板题. 这里直接讲述一下高斯消元的算法流程: 枚举每一列 \(c\): 找到第 \(c\) 列绝对值最大的一行: 将这一行换到最上面: 将该行的第一个数变成 \(1\): 将下面所有行 ...
- matlab的解方程的例子
syms x y z=exp(2*x+y)+cos(3*x*y)-exp(1)-1; zz=subs(z,x,1) solve(zz)
随机推荐
- unity3d格式的导出与加载
http://blog.csdn.net/nateyang/article/details/7567831 1.导出.unity3d格式资源: http://game.ceeger.com/Scrip ...
- hdu 3572 Task Schedule(最大流&&建图经典&&dinic)
Task Schedule Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) To ...
- PgSql备份pg_dump与还原手记pg_restore(转)
可以直接跳转至最后面的示例进行查看 真没有想到,以前一直是PostgreSQL使用者,突然需要库移植又成了头一招了!原来它与mysql命令行操作区别还挺大. 不用怕,但绝对要细心,因为数据库操作是网站 ...
- 最长公共子序列(LCS)问题 Longest Common Subsequence 与最长公告字串 longest common substr
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列.令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk ...
- Opengl ES 1.x NDK实例开发之六:纹理贴图
开发框架介绍请參见:Opengl ES NDK实例开发之中的一个:搭建开发框架 本章在第三章(Opengl ES 1.x NDK实例开发之三:多边形的旋转)的基础上演示怎样使用纹理贴图,分别实现了三角 ...
- Git-在一个电脑上同时使用两个Git的账号
前言 又需要登录公司的账号,又想在电脑上使用自己的账号. 实现 首先是git config方面的设置,要取消掉原本对于git账号的全局设置. git config --global --unset u ...
- mysql课程记录
thread_pool可以使用Percona的版本和Mariadb的版本 都是支持的 主从切换是根据HA的方式,TDDL(Taobao Distribute Data Layer) 的方式的话,推 ...
- linux 下vi /vim 中文汉字乱码解决
http://my.oschina.net/laserdance/blog/53474很多win下编译的配置文件(译码格式有utf8/gbk)上传到linux服务器上时打开汉字乱码 解决方法如下: 修 ...
- 最实用、最常用的jQuery代码片段
// chinacoder.cn JavaScript Document $(document).ready(function() { //.filter(":not(:has(.selec ...
- Python Kivy 安装问题解决
Fix: Running this was suggested by @matham in #3889 and solves the problem described below:python -m ...
