【拓扑排序】【DFS】Painting A Board

[poj1691]Painting A Board

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3902		Accepted: 1924

Description

The CE digital company has built an Automatic Painting Machine (APM) to paint a flat board fully covered by adjacent non-overlapping rectangles of different sizes each with a predefined color. 

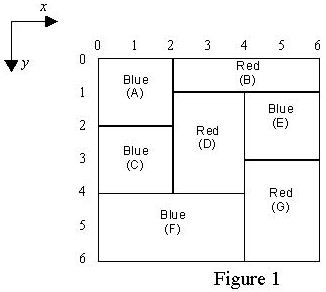
To color the board, the APM has access to a set of brushes. Each brush has a distinct color C. The APM picks one brush with color C and paints all possible rectangles having predefined color C with the following restrictions: 
To avoid leaking the paints and mixing colors, a rectangle can only be painted if all rectangles immediately above it have already been painted. For example rectangle labeled F in Figure 1 is painted only after rectangles C and D are painted. Note that each rectangle must be painted at once, i.e. partial painting of one rectangle is not allowed. 
You are to write a program for APM to paint a given board so that the number of brush pick-ups is minimum. Notice that if one brush is picked up more than once, all pick-ups are counted. 

Input

The first line of the input file contains an integer M which is the number of test cases to solve (1 <= M <= 10). For each test case, the first line contains an integer N, the number of rectangles, followed by N lines describing the rectangles. Each rectangle R is specified by 5 integers in one line: the y and x coordinates of the upper left corner of R, the y and x coordinates of the lower right corner of R, followed by the color-code of R. 
Note that: 

1. Color-code is an integer in the range of 1 .. 20.
2. Upper left corner of the board coordinates is always (0,0).
3. Coordinates are in the range of 0 .. 99.
4. N is in the range of 1..15.

Output

One line for each test case showing the minimum number of brush pick-ups.

Sample Input

1
7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

Sample Output

3

Source

Tehran 1999

 

题目大意：给一个板子，涂下面的板子前要先涂完上面所有与之相邻的。同一种画笔拿起一次算一次使用，请问最少多少次涂完画板？

试题分析：建图，求所有的拓扑序后每个拓扑序暴力求解次数，找最少的就好了

 

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
inline int read(){
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
int T;
bool dis[41][41];

int x1[41],y1[41],x2[41],y2[41],col[41];
int N,res,ans=999999;
int tu[41];
bool vis[41];
int que[41];

void dfs(int st){
	if(st==N) {
	    res=0;
	    for(int k=1;k<=N;k++) if(que[k]!=que[k-1]) res++;
		ans=min(ans,res);
		return ;
	}
	for(int i=1;i<=N;i++){
		if(!tu[i]&&!vis[i]){
			for(int j=1;j<=N;j++) if(dis[i][j]) tu[j]--;
			vis[i]=true;que[st+1]=col[i];
			dfs(st+1);
			vis[i]=false;
			for(int j=1;j<=N;j++) if(dis[i][j]) tu[j]++;
		}
	}
	return ;
}

int main(){
    T=read();
    while(T--){
    	ans=999999;
    	memset(tu,0,sizeof(tu));
    	memset(dis,false,sizeof(dis));
        N=read();
        for(int i=1;i<=N;i++){
            x1[i]=read(),y1[i]=read();
            x2[i]=read(),y2[i]=read();
            col[i]=read();
        }
        for(int i=1;i<=N;i++){
        	for(int j=1;j<=N;j++)
                if(i!=j&&x2[j]==x1[i]&&((y1[i]>=y1[j]&&y1[i]<=y2[j])||(y2[i]<=y2[j]&&y2[i]>=y1[j])||(y1[i]<=y1[j]&&y2[i]>=y2[j])||(y1[i]>=y1[j]&&y2[i]<=y2[j]))) dis[j][i]=true,tu[i]++;
		}
		dfs(0);
        printf("%d\n",ans);
    }
}