POJ 3519 Minimal Backgammon

Minimal Backgammon

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 1195		Accepted: 700		Special Judge

Description

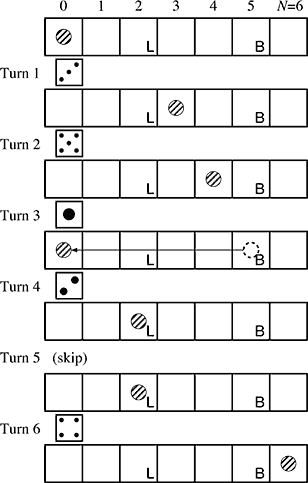Figure 2: An example game

Here is a very simple variation of the game backgammon, named “Minimal Backgammon”. The game is played by only one player, using only one of the dice and only one checker (the token used by the player).

The game board is a line of (N + 1) squares labeled as 0 (the start) to N (the goal). At the beginning, the checker is placed on the start (square 0). The aim of the game is to bring the checker to the goal (square N). The checker proceeds as many squares as the roll of the dice. The dice generates six integers from 1 to 6 with equal probability.

The checker should not go beyond the goal. If the roll of the dice would bring the checker beyond the goal, the checker retreats from the goal as many squares as the excess. For example, if the checker is placed at the square (N − 3), the roll “5” brings the checker to the square (N − 2), because the excess beyond the goal is 2. At the next turn, the checker proceeds toward the goal as usual.

Each square, except the start and the goal, may be given one of the following two special instructions.

• Lose one turn (labeled “L” in Figure 2)
  If the checker stops here, you cannot move the checker in the next turn.

• Go back to the start (labeled “B” in Figure 2)
  If the checker stops here, the checker is brought back to the start.

Given a game board configuration (the size N, and the placement of the special instructions), you are requested to compute the probability with which the game succeeds within a given number of turns.

Input

The input consists of multiple datasets, each containing integers in the following format.

N T L B
Lose₁
⋯
Lose_L
Back₁
⋯
Back_B

N is the index of the goal, which satisfies 5 ≤ N ≤ 100. T is the number of turns. You are requested to compute the probability of success within T turns. T satisfies 1 ≤ T ≤ 100. L is the number of squares marked “Lose one turn”, which satisfies 0 ≤ L ≤ N − 1. B is the number of squares marked “Go back to the start”, which satisfies 0 ≤ B ≤ N − 1. They are separated by a space.

Lose_i’s are the indexes of the squares marked “Lose one turn”, which satisfy 1 ≤ Lose_i ≤ N − 1. All Lose_i’s are distinct, and sorted in ascending order. Back_i’s are the indexes of the squares marked “Go back to the start”, which satisfy 1 ≤ Back_i ≤ N − 1. All Back_i’s are distinct, and sorted in ascending order. No numbers occur both in Lose_i’s and Back_i’s.

The end of the input is indicated by a line containing four zeros separated by a space.

Output

For each dataset, you should answer the probability with which the game succeeds within the given number of turns. The output should not contain an error greater than 0.00001.

Sample Input

6 1 0 0
7 1 0 0
7 2 0 0
6 6 1 1
2
5
7 10 0 6
1
2
3
4
5
6
0 0 0 0

Sample Output

0.166667
0.000000
0.166667
0.619642
0.000000
题目大意：第一行输入N,T,L,B,表示总共有编号为0-N的一排格子，N号格子为目标格子，其中有L个格子走到那些格子上要停止一次，B个格子，走到那些格子上就要直接返回到0号格子，紧接着输入L个数字表示要停止一次的格子的编号，后面是B个数字，表示要返回到0号格子的格子的编号，每一轮抛一枚骰子，骰子上是多少就前进几步，如果超出了编号为N的格子，则开始后退，问在T轮之内到达目标格子的概率。
解题方法：概率DP,dp[i][j]代表第i轮走到第j号格子的概率。

#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;

double dp[][];//dp[i][j]代表第i轮走到第j号格子的概率

int main()
{
    int Back[], Lose[], N, T, L, B, index;
    while(scanf("%d%d%d%d", &N, &T, &L, &B) != EOF)
    {
        if (N ==  && T ==  && L ==  && B == )
        {
            break;
        }
        memset(dp, , sizeof(dp));
        memset(Back, , sizeof(Back));
        memset(Lose, , sizeof(Lose));
        for (int i = ; i < L; i++)
        {
            scanf("%d", &index);
            Lose[index] = ;//要停止一次的格子的编号
        }
        for (int i = ; i < B; i++)
        {
            scanf("%d", &index);
            Back[index] = ;//要返回的格子的编号
        }
        dp[][] = ;
        for (int i = ; i < T; i++)
        {
            for (int j = N - ; j >= ; j--)
            {
                if (dp[i][j] == )//如果第i轮到达j号格子的概率为0，则直接忽略
                {
                    continue;
                }
                if (Back[j] == )
                {//走到j号格子要返回0号格子，则第i步走到0号格子的概率加上dp[i][j]
                    dp[i][] += dp[i][j];
                }
                else
                {
                    if (Lose[j] == )//如果走到j号格子要停止一次，直接跳过第i + 1轮
                    {
                        for (int k = ; k <= ; k++)
                        {
                            if (j + k <= N)
                            {
                                dp[i + ][j + k] += dp[i][j] / ;
                            }
                            else
                            {//如果走到超过最大值N，则从N开始后退
                                dp[i + ][ * N - j - k] += dp[i][j] / ;
                            }
                        }
                    }
                    else
                    {
                        for (int k = ; k <= ; k++)
                        {
                            if (j + k <= N)
                            {
                                dp[i + ][j + k] += dp[i][j] / ;
                            }
                            else
                            {
                                dp[i + ][ * N - j - k] += dp[i][j] / ;
                            }
                        }
                    }
                }
            }
        }
        double ans = ;
        //从第1轮到第T轮到达终点的概率之和，因为每一轮都有可能到达终点
        for (int i = ; i <= T; i++)
        {
            ans += dp[i][N];
        }
        printf("%.6f\n", ans);
    }
    return ;
}