vijos1144（小胖守皇宫）

也是ural1039

描述

huyichen世子事件后，xuzhenyi成了皇上特聘的御前一品侍卫。

皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；某些宫殿间可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。

可是xuzhenyi手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

帮助xuzhenyi布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

格式

输入格式

输入文件中数据表示一棵树，描述如下：

第1行 n，表示树中结点的数目。

第2行至第n+1n+1行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号i（0<i≤n0<i≤n），在该宫殿安置侍卫所需的经费k，该点的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1,r2,⋯,rmr1,r2,⋯,rm。

对于一个n（0<n≤15000<n≤1500）个结点的树，结点标号在1到n之间，且标号不重复。保证经费总和不超过231−1231−1。

输出格式

输出文件仅包含一个数，为所求的最少的经费。

样例1

样例输入1[复制]

 

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

样例输出1[复制]

 

25

限制

 

提示

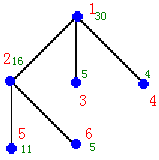
选择3,4,2费用最小为25

来源

huyichen

---

题解

有一棵树，每个点或者相邻的点必须要驻扎人，求驻扎总费用最小，典型的树形动规

分析

对于节点i,有三种状态：1、自守   2、子守  3、父守

方程:

f[i,1]:=Σ(min{f[son,1],f[son,2],f[son,3]})+a[i]

f[i,2]:=Σ(min{f[son,1],f[son,2]})+m 　　　//m的意思是所有son的自守与子守的差最小值，如果大于0就要加上这说明没有一个儿子是自守，不符合定义，就必须加上m，算作这个儿子守

f[i,3]:=Σ(f[son,2])　　　　　　　　　 //son的自守情况已经被上面的情况包含了

第2种情况要特别注意,要求它的子结点中必须有一个是1状况的,所以令m=min{f[son[j],1]-f[son[j],2]},如果m>0说明在决策的时候，它的子结点没有一个是1状况的，这样就要加上m,否则令m=0.

这个方程看了一下午久才懂

AC代码

#include<iostream>
#include<cstdio>
#define MAX 1000000000
using namespace std;
int root,n,tot=,num,c,m,kk;
int cost[];
int head[];
int from[];
int to[];
int f[][];// 1自守,2子守,3父守
void add(int a,int b)
{
    tot++;
    to[tot]=b;
    from[tot]=head[a];
    head[a]=tot;
}
int _min(int a,int b)
{
    return a<b?a:b;
}
void treedp(int x)
{
    if(head[x]==)//叶子节点
    {
        f[x][]=f[x][]=cost[x];
        return;
    }
    int m,t;
    f[x][]=cost[x];
    f[x][]=f[x][]=;
    m=MAX;
    while(head[x]>)
    {
        t=to[head[x]];
        treedp(t);
        f[x][]=f[x][]+_min(f[t][],_min(f[t][],f[t][]));
        f[x][]=f[x][]+_min(f[t][],f[t][]);
        f[x][]=f[x][]+f[t][];
        if(m>f[t][]-f[t][])
            m=f[t][]-f[t][];
        head[x]=from[head[x]];
    }
    if(m>) f[x][]+=m;
}
int main()
{
    scanf("%d",&n);
    root=n*(n+)/;
    for(int i=;i<=n;i++)
    {
        scanf("%d%d%d",&num,&c,&m);
        cost[num]=c;
        for(int j=;j<=m;j++)
        {
            scanf("%d",&kk);
            root-=kk;
            add(num,kk);
        }
    }
    treedp(root);
    cout<<_min(f[root][],f[root][]);
    return ;
}