Floyd 求最短路（poj 1161）

Floyd-Warshall算法介绍：

Floyd-Warshall算法的原理是动态规划。

设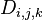为从到的只以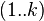集合中的节点为中间节点的最短路径的长度。

1. 若最短路径经过点k，则；
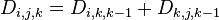2. 若最短路径不经过点k，则。

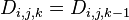因此，。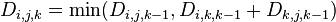

在实际算法中，为了节约空间，可以直接在原来空间上进行迭代，这样空间可降至二维。

 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
 for each vertex v
    dist[v][v] ←
 for each edge (u,v)
    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
 for k from  to |V|
    for i from  to |V|
       for j from  to |V|
          if dist[i][j] > dist[i][k] + dist[k][j]
             dist[i][j] ← dist[i][k] + dist[k][j]
         end if

题目：Walls

题意：给定一个图，求其中几个点相连最少要穿越的边数。

思路：这题的图要重新建，不能用原图，新图是这样的：将一个圈化为点，之间的关系是两个圈是否有公共边，然后就是求最短路问题了；

#include <iostream>
#include <algorithm>
#include <stdlib.h>
#include <time.h>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <set>

#define c_false ios_base::sync_with_stdio(false); cin.tie(0)
#define INF 0x3f3f3f3f
#define INFL 0x3f3f3f3f3f3f3f3f
#define zero_(x,y) memset(x , y , sizeof(x))
#define zero(x) memset(x , 0 , sizeof(x))
#define MAX(x) memset(x , 0x3f ,sizeof(x))
#define swa(x,y) {LL s;s=x;x=y;y=s;}
using namespace std ;
#define N 500

const double PI = acos(-1.0);
typedef long long LL ;
int mapp[N][N], region[N][N], p_num[N], n, m, r;
struct Person{
    int adr;
    int t;      ///所在环数；
    int reg[N]; ///环
}person[N];

int find_dis(int i, int j){  ///寻找i,j 两区域间的边，若没有，返回-1
    int ii, jj;
    for(ii = ; ii <= p_num[i]; ii++){
        for(jj = ; jj <= p_num[j]; jj++){
            if(region[i][ii] == region[j][jj]){
                if(region[i][ii+] == region[j][jj+] || region[i][ii+] == region[j][jj-] ||
                   region[i][ii-] == region[j][jj+] || region[i][ii-] == region[j][jj-])
                    return ;
            }
        }
    }
    return -;
}

void Floyd(){ 　　　　///寻找最短路
    int i, j, k;
    for(k = ; k<= m; k++)
        for(i = ; i<= m; i++)
            for(j = ; j<= m; j++)
                mapp[i][j] = mapp[j][i] = min(mapp[i][j], mapp[i][k]+mapp[k][j]);
}

int search_(int i){  //查找i区域到俱乐部每个成员间的距离和；
    int j, k, s = ;
    for(j = ; j<= r;j++){
        int d = INF;
        for(k = ; k <=person[j].t; k++)
            d = min(d, mapp[person[j].reg[k]][i]);
        s+=d;
    }
    return s;
}
int main(){
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int i,j,k;
    while(~scanf("%d",&m)){
        scanf("%d%d",&n,&r);
        for(i = ; i<= r;i++){
            scanf("%d",&person[i].adr);
            person[i].t = ;
        }
        for(i = ; i <= m; i++){
            scanf("%d", &p_num[i]);
            for(j = ; j <= p_num[i]; j++){
                scanf("%d", &region[i][j]);
                for(k = ; k <= r; k++){
                    if(person[k].adr == region[i][j])
                        person[k].reg[ ++person[k].t] = i;
                }
            }
            region[i][] = region[i][ p_num[i] ];
            region[i][p_num[i]+] = region[i][];
        }
        for(i = ; i <= m; i++){
            for(j = ; j<=m; j++){
                if(i == j){
                    mapp[i][j] = mapp[j][i] = ;continue;
                }
                int ans = find_dis(i, j);
                if(ans == ) mapp[i][j] = mapp[j][i] =;
                else mapp[i][j] = mapp[j][i] =INF;
            }
        }
        Floyd();
        int min_dis = search_();
        for(i = ; i <=m ;i++){
            int  d =search_(i);
            min_dis = min(d, min_dis);
        }
        printf("%d\n",min_dis);
    }
    return ;
}