Boyer-Moore Majority Vote Algorithm

介绍算法之前, 我们来看一个场景, 假设您有一个未排序的列表。您想知道列表中是否存在一个数量占列表的总数一半以上的元素, 我们称这样一个列表元素为 Majority 元素.如果有这样一个元素, 求出它？如果没有，你需要知道没有。你想要尽可能高效地完成这个工作。

这个问题的一个常见场景可能是容错计算。您执行多个冗余计算，然后验证大多数结果是否一致。

Boyer-Moore Majority Vote Algorithm

算法描述

Boyer-Moore 算法在 Boyer-Moore Majority Vote Algorithm 中提出。该算法使用 O（1）额外空间和 O（N）时间。它只需要遍历输入列表中2遍。实现这一点也很简单，虽然有点麻烦来了解它的工作原理。

第一次遍历列表，会生成 Majority 元素的候选值。第二遍只是计算该元素的频数以确认是否是 Majority 元素。第一遍是有趣的部分。

在第一遍，我们需要2个值：

候选值 candidate，初始设置可以为任何值。
一个计数器 count，初始设置为0。
对于输入列表中的每个元素，我们首先检查计数值。如果计数等于0，我们将候选值设置为当前元素的值。接下来，首先将元素的值与当前候选值进行比较。如果它们相同，我们将计数加1.如果它们不同，我们计数减1。

在python：


candidate = 0
count = 0

//// 第 1 次遍历
for value in List:
  if count == 0:
    candidate = value
  if candidate == value:
    count += 1
  else:
    count -= 1

// 第 2 次遍历
Majority = num.count(candidate)
if (Majority > List.size/2):
  return Majority

第 1 遍遍历结束时，如果存在 Majority，候选值将是 Majority。第二次遍历可以验证候选值 candidate 是否是 Majority。

算法解析

为了看这是如何工作的，我们只需要考虑包含 Majority 的情况。如果该列表不包含 Majority 元素，则第二次遍历会轻易地拒绝该候选者。

首先，考虑第一个元素不是 Majority 元素的列表，例如，Majority为 0 的列表：

[5，5，0，0，0，5，0，0，5]

当处理第一个元素时，我们将 5 分配给候选值，计数器初始化为 1。由于 5 不是 Majority，在遍历到列表的最后一个元素之前的某个时刻，count将会下降到 0。在上面的例子中，这发生在第 4 个元素：

列表值：
[5，5，0，0，...

计数值：
[1，2，1，0，...

在计数返回到 0 的时候，我们已经消耗了和元素 5 相同数量的其他元素。如果所有其他元素都是这种情况下的 Majority 元素，那么我们已经消耗了2个Majority 元素和2个非Majority元素。这是我们可以消费的最多的Majority元素，但即使这样, Majority 元素仍然是输入列表剩余部分的大部分（在我们的示例中，余数为... 0，5，0，0， 5]）。

我们可以看到，如果第一个元素是多数元素，并且在某个时间点计数器下降到 0，那么我们还可以看到，多数元素仍然是输入列表剩余部分的大部分，因为我们再次消耗了相等数的Majority元素和非Majority元素。

这反过来证明了当列表前面候选值计数器降到 0 时, 会被丢弃，而不会影响算法的第一遍的最终结果。我们可以一遍又一遍地重复地抛弃我们前面输入的范围，直到找到一个范围，该范围是我们输入的后缀，其中count不会下降到0。

给定一个输入列表后缀，其中 count 从不下降到 0，我们必须有更多的值等于第一个元素，而不是不值的值。因此，第一个元素（候选值）必须是该列表的 Majority，并且是输入列表中的 Majority 的唯一可能的候选值，尽管仍然可能没有 Majority。

Majority Element II

此题来自 leetcode 229 Majority Element II

问题描述:

Given an integer array of size n, find all elements that appear more than ⌊ n/3 ⌋ times. The algorithm should run in linear time and in O(1) space.

给定一个大小为 n 的整数数组，找到所有出现超过 ⌊n / 3⌋次的元素。该算法应在线性时间 O(n) 和额外的 O（1）空间复杂度

思路: 首先就是看看列表中最多会有几个这样的 Majority 元素, 由于这里的 Majority 元素的为频数大于 ⌊n / 3⌋, 所以这样的元素最多有 2 个. 下面是 Most voted Solution, 灵活的使用的了 Boyer-Moore Voted Algorithm.

class Solution:

def majorityElement(self, nums):
    if not nums:
        return []
    count1, count2, candidate1, candidate2 = 0, 0, 0, 1

    // 第一轮循环
    for n in nums:
        if n == candidate1:
            count1 += 1
        elif n == candidate2:
            count2 += 1
        elif count1 == 0:
            candidate1, count1 = n, 1
        elif count2 == 0:
            candidate2, count2 = n, 1
        else:
            count1, count2 = count1 - 1, count2 - 1
    // 第二轮循环
    res = [n for n in (candidate1, candidate2) if nums.count(n) > len(nums) // 3]

    return res

上述代码第一轮循环之后, 会选出 2 个 Majority 候选值, 这会有 3 种情况:

列表没有 Majority 元素, 那么第一轮选出的候选值在第二轮都会被淘汰
列表只有 1 个 Majority 元素, 那么第一轮选出的 2 个候选值会有 1 个在第二轮都会被淘汰
列表有 2 个 Majority 元素, 那么第一轮选出的 2 个候选值都是 Majority, 第二轮自然没法淘汰任何一个

上面第 1 种情况中, 由于列表没有 Majority 元素, 自然没有元素的频数大于 ⌊n / 3⌋, 第二轮 2 个候选值都会被淘汰. 难缠的是第 2 种情况, 所以放在最后, 下面先说第 3 种情况

第 3 种情况, 列表中有 2 个 Majority 元素, 两个加起来的数量至少是列表元素的 2/3 以上, 按照 Boyer-Moore Voted Algorithm 中基本概念是 “让我们取消彼此的投票", 所以列表其他元素总数少于总数的 1/3, 所以不可能否决 2 个 Majority 元素中的任何一个, 自然选出来的元素就是 Majority 元素. 下面来说说第二种情况

第 2 种情况中, 列表只有 1 个 Majority 元素, 数量是超过列表元素的 1/3, 那么这时候列表中其他元素总数可能会大于 Majority 元素, 那我们选择的候选值中会包括 Majority 元素吗? 答案是肯定的, 那么我们看看为什么是这样.

为了便于说明, 我们基于一个观察将问题等价转化为一个便于描述的情况. 我们观察到, 给予你一个列表 A, 如果该列表有 Majority 元素, 那么改变列表中元素的排列顺序得到列表 B, 那么列表 A 的 Majority 元素与列表 B 相同, 当然这是个显而易见的, 因为我们判断 Majority 元素的依据是元素出现的频数.

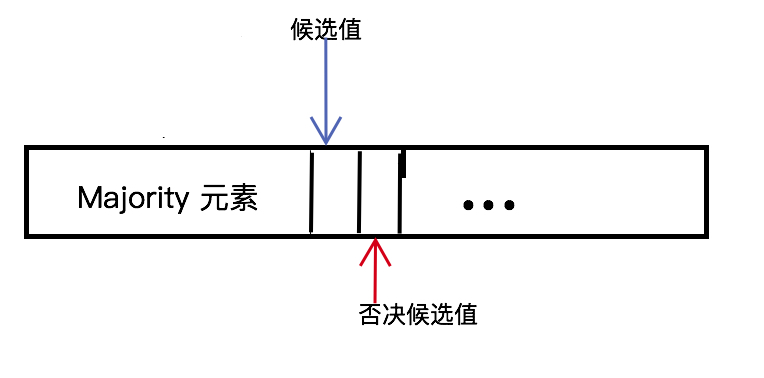
既然如此, 列表只有 1 个 Majority 元素, 我们假设列表的 Majority 元素都排在列表的开始位置, 那么非 Majority 元素想要投票否决 Majority 元素需要超过列表 1/3 的数量, 这乍看起来是有可能的, 不过实际上是不可能的, 由于我们选举了 2 个候选值, 因为上面 if/else 选择结构的逻辑是当输入元素不是2个候选值中的任何一个且2个候选值的计数器都不为1时, 才会将2个候选值的计数器减 1, 也就是说只有 1 个 Majority 元素的列表的另一个候选值是非Majority 元素, 并且会被其他非Majority 元素投票否决. 我们可以假设列表除去头部的 Majority 元素, 其他的元素都不相等, 当遍历列表元素到第一个非Majority 元素时, 元素别选举为候选值这时Majority 元素的计数器不变), 然后又被否决(这时Majority 元素的计数器也会减去1), 依次进行下去, 总数最多不超过 2n/3 - 2 的非Majority元素一般当选了候选值, 一半用来否决, 二者一半总数不会超过 n/3 -1, 没法否决掉总数超过 n/3 的Majority元素, 所以最终 Majority 元素会在候选值中, 第二轮循环被选出.

摘自多数投票算法