POJ 1661 Help Jimmy(DP,注意边界)

Help Jimmy

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9399		Accepted: 3025

Description

"Help Jimmy" 是在下图所看到的的场景上完毕的游戏。 




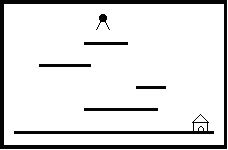
场景中包含多个长度和高度各不同样的平台。

地面是最低的平台，高度为零，长度无限。 



Jimmy老鼠在时刻0从高于全部平台的某处開始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑。它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时。開始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。 



设计一个程序。计算Jimmy究竟地面时可能的最早时间。 

Input

第一行是測试数据的组数t（0 <= t <= 20）。每组測试数据的第一行是四个整数N。X。Y，MAX。用空格分隔。N是平台的数目（不包含地面），X和Y是Jimmy開始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描写叙述一个平台，包含三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。

1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i
= 1..N）。全部坐标的单位都是米。 



Jimmy的大小和平台的厚度均忽略不计。假设Jimmy恰好落在某个平台的边缘，被视为落在平台上。

全部的平台均不重叠或相连。測试数据保证问题一定有解。

Output

对输入的每组測试数据。输出一个整数。Jimmy究竟地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output

23

Source

POJ Monthly--2004.05.15 CEOI 2000

注意 [-10,10],[10,20],这两个平台在高度同意的情况下是能够跳的。

。

。

。被坑了好久

#include <iostream>
#include <fstream>
#include <string>
#include <time.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <stack>
#include <cstring>
#include <cmath>
#include <set>
#include <vector>
using namespace std;
#define INF 0x7fffffff
int n,x,y,maxn;
int dp[1111][2];//dp[i][0]表示到达i平台左端点最小值,dp[i][1]表示右端点最小值
bool vist[1111][2];
struct node{
	int l;
	int r;
	int h;
}dian[1111];

int cmp(const node &a,const node &b){
	return a.h>b.h;
}
int main() {
 //  freopen("G://test.txt","r",stdin);
	int t;
	scanf("%d",&t);
	while(t--){
    scanf("%d%d%d%d",&n,&x,&y,&maxn);
		memset(vist,false,sizeof(vist));
		dian[0].l=x;
		dian[0].r=x;
		dian[0].h=y;
		dp[0][0]=0;
		dp[0][1]=0;
		for(int i=1;i<=n;++i){
			scanf("%d%d%d",&dian[i].l,&dian[i].r,&dian[i].h);
			dp[i][0]=dp[i][1]=INF;
		}
		sort(dian+1,dian+n+1,cmp);
		for(int i=1;i<=n;++i){
			for(int j=0;j<i;++j){//枚举比i高的或者相等的（相等的以下if给T掉了）
				if(vist[j][0]==false){
					if(dian[j].h>dian[i].h&&dian[j].h-dian[i].h<=maxn&&dian[j].l>=dian[i].l&&dian[j].l<=dian[i].r){
						vist[j][0]=true;
						if(dp[j][0]==INF)
							continue;
						dp[i][0]=min(dp[i][0],dp[j][0]+dian[j].l-dian[i].l);
						dp[i][1]=min(dp[i][1],dp[j][0]+dian[i].r-dian[j].l);
					}
				}//左边

				if(vist[j][1]==false){
					if(dian[j].h>dian[i].h&&dian[j].h-dian[i].h<=maxn&&dian[j].r>=dian[i].l&&dian[j].r<=dian[i].r){
						vist[j][1]=true;
						if(dp[j][1]==INF)
							continue;
						dp[i][0]=min(dp[i][0],dp[j][1]+dian[j].r-dian[i].l);
						dp[i][1]=min(dp[i][1],dp[j][1]+dian[i].r-dian[j].r);
					}
				}//右边
			}//for
		}//for

		int ans=INF;
		for(int i=0;i<=n;++i){
			if(vist[i][0]==false&&dian[i].h<=maxn)
				ans=min(ans,dp[i][0]);
			if(vist[i][1]==false&&dian[i].h<=maxn)
				ans=min(ans,dp[i][1]);
		}
		if(ans==INF){
			printf("大兄弟。

。。大于等于这个边界我也是跪了\n");

		}
		else
		printf("%d\n",ans+y);

    }
    return 0;
}