深入浅出数据结构C语言版（14）——散列表

　　我们知道，由于二叉树的特性（完美情况下每次比较可以排除一半数据），对其进行查找算是比较快的了，时间复杂度为O(logN)。但是，是否存在支持时间复杂度为常数级别的查找的数据结构呢？答案是存在，那就是散列表（hash table，又叫哈希表）。散列表可以支持O(1)的插入，理想情况下可以支持O(1)的查找与删除。

　　散列表的基本思想很简单：

　　1.设计一个散列函数，其输入为数据的关键字，输出为散列值n（正整数），不同数据关键字必得出不同散列值n（即要求散列函数符合单射）

　　2.创建一个数组HashTable（即散列表），插入的数据存储在HashTable[n]中，n为数据的散列值且小于散列表的最大下标

　　这样一来，插入数据只需要计算出数据的散列值n，而后将数据存至HashTable[n]。查找数据则根据数据计算出散列值n，而后检查HashTable[n]是否存有数据即可，删除同理。这些操作都是O(1)。

　　但是稍加思索就会发现，上述思想是不可能在任意情况下都实现的：

　　一来，不可能任意情况下都有单射的散列函数，比如数据关键字为任意整数时，关键字-a与a该如何映射？

　　二来，即使散列函数是单射，散列表的大小也不可能总是保证大于所有可能的散列值，比如数据关键字为正整数，那么散列函数只需要令散列值等于数据关键字即可保证单射，但是如果数据总量为1000，而数据的可能最大值为10000000，难道我们创建一个大小为10000000的散列表吗？

　　也就是说，我们实际实现散列表时，必须面对这两个问题：

　　1.如何实现一个尽可能“接近”单射的散列函数

　　2.当不同数据关键字散列值相同时，如何处理这种冲突

　　第一个问题显然是因情而异的，只有给定了数据类型和一定的数据特性，才能写出对应的、好的散列函数。比如数据的key为随机正整数时，简单的散列函数是直接返回key%tableSize，这样做也没有多大问题。但是如果知道散列表的tableSize为100，且数据的key个位和十位必然为0，那么这样的散列函数就是不行的，必须修改。

　　也就是说，第一个问题是不存在普适性解法的，实现一个良好的散列函数本身又是另一件算法设计的事情，所以我们对于第一个问题不进行深入讨论。接下来的讨论假定这样的情形：输入的数据（关键字）为长度不超过20的字符串，且散列函数如下：

//简单的散列函数，将字符串中字符的ASCII码值相加，然后返回其与tableSize求余后的结果
unsigned int Hash(const char *target,unsigned int tableSize)
{
    unsigned int HashVal = ;
    while (*target != '\0')
        HashVal += *target++;

    return HashVal%tableSize;
}

　　那么第二个问题呢？当不同数据映射到相同散列值时的冲突，是否存在普适性的解法？答案是存在，并且解法有很多种（但是此处只给出一种的代码，其他解法只提出思路）

　　常见的处理散列冲突的解法有三种：分离链接，开放定址，双散列。我们将给出分离链接法的代码，其他两种则略做讨论。

　　分离链接法的思想很简单：如果多个数据都映射到了n，那就让这多个数据都待在HashTable[n]。

　　显然，要让多个数据都待在HashTable[n]处，那么HashTable的元素类型必然不是与数据相同的类型（如果是的话，HashTable[n]处只可能存下一个数据），而应该是一个链表。

　　举例来说，假定tableSize为7，根据已给的散列函数，关键字"ac"和"bb"的散列值均为0，则散列表在插入"ac"和"bb"后应如下：

　　

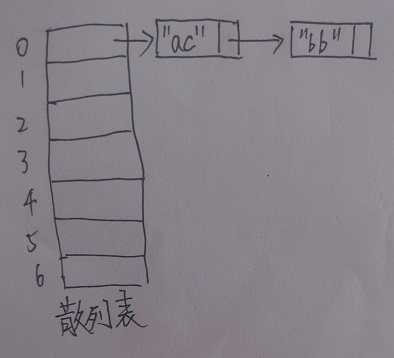
　　那么使用分离链接的散列表的查找方法也就是：计算出给定数据的散列值n，找到HashTable[n]（一个链表），在HashTable[n]这个链表中遍历，查找是否存在给定数据。删除的实现则是在查找的基础上实施链表的删除方法即可。

　　不难看出，良好的散列函数是极其重要的，假设散列函数总是给出相同的散列值，那么使用分离链接法的散列表最终就成了一个链表（所有数据都映射散列值n，于是所有数据都存储在了链表HashTable[n]中）

　　现在，我们可以开始一步步实现一个散列表了，其散列函数我们在上面已经给出，其处理冲突的方法为分离链接。

　　首先，HashTable的元素是链表，所以必须给出链表结点的定义：

#define STRSIZE 20

struct ListNode {
    char str[STRSIZE];
    struct ListNode *next;
};
typedef struct ListNode *List;
typedef List Position;   //Position用于查找和删除

　　接下来是设计HashTable本身，即确定HashTable的元素类型，最简单的办法是令struct ListNode作为HashTable的类型：

struct ListNode HashTable[TABLESIZE];

　　但这样将带来一个问题：如何判断HashTable[n]中是空的还是只有一个元素？所以我们令List作为HashTable的元素类型，即令HashTable的元素为指向链表第一个元素的指针。这样一来，如果HashTable[n]处的链表为空，则HashTable[n]就等于NULL。

List HashTable[TABLESIZE];

　　但是为了使我们的散列表更有适应性，我们希望令tableSize作为一个变量，即散列表的大小可以根据编程需要来给定，于是我们将散列表设计成如下结构，并在程序中使用指针来访问散列表。同时，我们给出初始化散列表的代码：

struct HashTbl {
    unsigned int size;
    List *table;  //table才是真正的那个散列表
};
typedef struct HashTbl *HashTable;  //我们访问散列表将通过指针，因为例如查找这样的函数需要散列表作为参数，如果传入一个struct HashTbl，不如传入一个struct HashTbl *

//根据给定大小创建散列表
HashTable Initialize(unsigned int tableSize)
{
    //创建散列表头，并根据给定大小tableSize创建表头中的散列表
    HashTable h = (HashTable)malloc(sizeof(struct HashTbl));
    h->size = tableSize;
    h->table = (List *)malloc(sizeof(List)*tableSize);

    //将散列表的每个元素（指向链表第一个元素的指针）初始化为NULL
    for (int i = ;i < tableSize;++i)
        h->table[i] = NULL;

    return h;
}

　　接下来是插入操作的代码

//将字符串source插入到h中的散列表
void Insert(HashTable h, const char *source)
{
    //此处实质为Find()操作，但为了顺便求出source的散列值，我们不直接使用Find()
    //若source已在散列表中，我们直接返回
    unsigned int HashVal = Hash(source, h->size);
    Position p = h->table[HashVal];
    while (p != NULL && strcmp(p->str, source))
    {
        p = p->next;
    }
    if (p != NULL)
        return;

    //若source不在散列表中，我们计算source的散列值，并将source插入到散列表的对应位置
    Position newNode = (Position)malloc(sizeof(struct ListNode));
    strcpy_s(newNode->str, STRSIZE, source);
    newNode->next = h->table[HashVal];
    h->table[HashVal] = newNode;
}

　　查找和删除操作都不难（查找的代码在插入中已经实现了），此处不予赘述。

　　接下来我们谈谈什么是开放定址法。

　　首先，根据散列表的基本思想，如果一个数据散列值为n，那它就应该“定址”于HashTable[n]处，这也可以说是分离链接法的根本（既然你们散列值为n，那你们就都得待在HashTable[n]）

　　而开放定址法就顾名思义了，数据不再是“定址”的，一个数据关键字散列值为n，但其不一定位于HashTable[n]处。

　　开放定址法是这么做的：如果数据关键字散列值为n，则先尝试将其插入到HashTable[n]处，若HashTable[n]处已有数据，则插入到HashTable[(n+1)%tableSize]处，如果该处亦有数据，则插入到HashTable[(n+2)%tableSize]处，以此类推，直至遇到某处为空，插入数据至该处，或者走遍散列表依然没有空处，则插入失败。这样的插入称为“线性探测”

　　查找操作则是：计算散列值n，比较HashTable[n]与数据，若相同则找到，否则比较HashTable[(n+1)%tableSize]与数据，以此类推，直至到了某个空结点，则说明没找到

　　删除操作则必须是懒惰删除，因为若实质删除，则开放定址法的插入和查找都将乱套，也就是说HashTable的元素类型必然是一个包含数据类型的新结构体，其存在frequency域用于表示数据是否存在或相同数据存在多少个。

　　

　　开放定址法相比于分离链接法可以节省指针空间，但也带来了两个问题：

　　1.如果插入数据时，总是按照n=n+1的形式去找一个空的HashTable[n]，那么数据很容易出现“集中”现象。（比如插入三个散列值为80的数据，再插入两个散列值为81和83的数据，那么它们都将“挤在”HashTable[80]到HashTable[84]间）

　　2.设装填因子Ω=已插入数据个数/tableSize，那么Ω越接近于1，开放定址法的各项操作就越慢，而且很可能出现插入失败

　　对于第一个问题，有两种改善的办法，一种是采用“平方探测”形式的插入，即令n+=2*++n-1，而不是n=n+1，这样可以减少一次集中，但相同散列值的数据依然可能出现“二次集中”现象。另一种办法则是双散列，即出现冲突时令n=n*hash2(key)，本质上来说，平方探测、线性探测和双散列是相似的，都是在出现冲突时另寻一处存放数据，当然，这个另寻一处必须是可重现的。

　　对于第二个问题，解决办法是再散列，即当Ω大于一定程度后，重新创建新的、更大的散列表，而后将数据移至新散列表。也就是“再次散列”。

　　使用分离链接法的散列表的示例程序代码：

　　https://github.com/nchuXieWei/ForBlog-----HashTable