[SinGuLaRiTy] NOIP互测模拟赛

	源文件名	输入输出文件	时间限制	内存限制
淘气的cch	cch.cpp	cch.in/out	1500ms	600MB
高爆螺旋狗	hedog.cpp	hedog.in/out	1000ms	512MB
毁灭计划	destroy.cpp	destroy.in/out	3000ms	256MB

淘气的cch

题目描述

cch太淘气了，一天，SunIsMe发现他把yhn家的墙壁都重新粉刷了一遍，yhn家的每块墙壁可以被分成M*N块，每一块有一种颜色（可以用一个整数表示），cch每粉刷一面墙壁有且仅把某一矩形区域刷成自己想要的颜色。yhn回家发现cch在搞事情，把cch打了一顿解气后，发现cch很有艺术天赋啊，每一面墙都是一幅抽象派巨著啊！不过，yhn可不想让他的每一块墙壁长得不一样，于是他让cch把他涂过的墙壁重新粉刷成一样的。粉刷墙壁是要耗体力的，每次cch可以改变一块墙壁中某一块的颜色，让其加1或减1，cch还想至少让自己的一幅画保留下来（也就是说至少有一块墙壁不重新粉刷），不过cch觉得自己笨成yhn了，于是拜托可以轻松AK这套题的你来帮忙。

一句话题意：有若干个整数矩阵，要求选择一个矩阵，使得它与其他矩阵的距离之和最小，此处矩阵与矩阵的距离指对应位置上的整数之差的绝对值(至于矩阵怎么产生的请看样例解释)。

输入格式

第1行给出原来每块墙的长宽M，N，cch涂过的墙的数量K，和颜色的数量Q。

第2到M+1行，每行给出一个长度为N的整数串，表示原来每块墙壁的颜色。

第M+2到M+K+2行，每行五个整数ai，bi，ci，di，ei，表示cch涂过的第i块墙壁的（ai，bi）到（ci，di）这块矩形部分被ei覆盖。

输出格式

第1行，一个整数，表示最少的重新粉刷次数。

样例数据

样例输入1	样例输出1
3 3 2 3 0 0 0 0 0 0 0 0 0 1 1 2 2 1 2 2 3 3 2	10
样例输入2	样例输出2
5 5 3 10 1 2 3 4 5 5 1 2 3 4 4 5 1 2 3 3 4 5 1 2 2 3 4 5 1 1 1 3 4 6 1 2 3 3 5 1 3 3 4 9	59

<样例解释>

对于样例1,cch粉刷后产生了两个矩阵:

0 0 0 1 1 0 0 0 0

0 0 0 => 1 1 0 和 0 2 2

0 0 0 0 0 0 0 2 2

两个矩阵的距离就是(1-0)+(1-0)+(0-0)+(1-0)+(2-1)+(2-0)+(0-0)+(2-0)+(2-0)=10.

<数据范围>

对于所有数据，N,M<=1000, K<=300000, Q<=30。

解析

维护每一种颜色在每一面墙中出现次数和的二维前缀和，枚举选择的墙，记每一面墙与原墙的距离为Total，则Ans=Total-被修改的矩形中每一面墙与原墙的距离+被修改的矩形中其它的墙与被选择墙的距离，更新答案即可。

时间复杂度 O(MNQ+QK)

Code

#include<cstdio>

#include<iostream>

#include<cstring>

#include<algorithm>

#include<cmath>

#include<time.h>

using namespace std;

#define MAXN 1000

#define MAXM 1000

#define MAXK 300000

#define MAXQ 30

#define INF 0x3f3f3f3f

#define LLF 0x3f3f3f3f3f3f3f3fll

typedef long long int LL;

void Read(int &x){

    x=;char c=getchar();bool flag=;

    while(c<''||''<c){if(c=='-')flag=;c=getchar();}

    while(''<=c&&c<=''){x=x*+c-'';c=getchar();}

    if(flag)x=-x;

}

int M,N,K,Q;

int A[MAXK+],B[MAXK+],C[MAXK+],D[MAXK+],E[MAXK+];

LL num[MAXM+][MAXN+][MAXQ+];//第k种字符的数量

LL val[MAXM+][MAXN+][MAXQ+];//第k重字符的距离贡献

LL cnt[MAXM+][MAXN+];//(i,j)上的修改次数

int str[MAXM+][MAXN+];

LL Total;//每一种版本与原图的距离之和

LL query(int a,int b,int c,int d,int e){

    LL rn=Total;//假设一开始是初始矩形

    for(int i=;i<Q;++i){

        //加上当前版本覆盖矩形中和其它版本的距离

        rn+=abs(i-e)*(num[c][d][i]-num[a-][d][i]-num[c][b-][i]+num[a-][b-][i]);

        //减去当前版本覆盖矩形中原来的影响

        rn-=val[c][d][i]-val[a-][d][i]-val[c][b-][i]+val[a-][b-][i];

    }

    return rn;

}

int main(){

    freopen("cch.in","r",stdin);

    freopen("cch.out","w",stdout);

    Read(M),Read(N),Read(K),Read(Q);

    for(int i=;i<=M;++i)

        for(int j=;j<=N;++j)Read(str[i][j]);

    for(int i=;i<=K;++i){

        Read(A[i]),Read(B[i]),Read(C[i]),Read(D[i]),Read(E[i]);

        //差分

        ++num[A[i]][B[i]][E[i]],++num[C[i]+][D[i]+][E[i]];

        --num[C[i]+][B[i]][E[i]],--num[A[i]][D[i]+][E[i]];

    }

    //统计出每一个位置的字符数量

    for(int i=;i<=M;++i)

        for(int j=;j<=N;++j)

            for(int k=;k<Q;++k){

                num[i][j][k]+=num[i-][j][k]+num[i][j-][k]-num[i-][j-][k];

                cnt[i][j]+=num[i][j][k];

            }

    for(int i=;i<=M;++i)

        for(int j=;j<=N;++j)

            num[i][j][str[i][j]]+=K-cnt[i][j];

    //计算贡献

    Total=;

    for(int i=;i<=M;++i)

        for(int j=;j<=N;++j)

            for(int k=;k<Q;++k){

                val[i][j][k]=abs(k-str[i][j])*num[i][j][k];

                Total+=val[i][j][k];

            }

    //累加矩形前缀和

    for(int i=;i<=M;++i)

        for(int j=;j<=N;++j)

            for(int k=;k<Q;++k){

                num[i][j][k]+=num[i-][j][k]+num[i][j-][k]-num[i-][j-][k];

                val[i][j][k]+=val[i-][j][k]+val[i][j-][k]-val[i-][j-][k];

            }

    LL ans=LLF;

    for(int i=;i<=K;++i)

        ans=min(ans,query(A[i],B[i],C[i],D[i],E[i]));

    printf("%I64d\n",ans);

    //printf("%0.6lf\n",(double)clock()/CLOCKS_PER_SEC);

}

高爆螺旋狗

题目描述

社会主义阵营为了防御资本主义阵营的攻击，驯养了一只高爆螺旋狗，这只狗吃的火药越多，爆炸半径越大。如果资本主义的毒瘤 cch 带领他的克隆体进犯，会立马遭到螺旋狗的打击。

社会主义阵营的卫星会对战场拍摄二维图片 A。所谓‘图片’，是一个 N*N 的由小写字母组成的矩阵。Hineven 掌握 cch 的‘图片’是一个类似的由全小写字母组成，边长为 M 的二维矩阵 B，如果一个‘图片’R 中存在一种方案：挖出一块正方形区域使得其每个字母能与 B 中相同位置的字母一样,那么我们认为 B‘出现’在 R 中挖出的正方形区域内左上角一次。

cch 带着他的克隆体大军压境。Hineven 希望能用高爆螺旋狗一次消灭至少 K 只 cch 克隆体，高爆螺旋狗的爆炸范围是一个边长为 X 的正方形，并且可以直接作用在战场的任意地点，消灭‘出现’在作用范围内的所有 cch。但是每只 cch 克隆体的战斗力略有差别，位置为(i,j)的 cch 战斗力为整数 Cij，而高爆螺旋狗只能消灭战斗力在区间[L,R]内的 cch。L 和 R 满足等式 R-L=X-1。这意味着 Hineven 还要同时决定 L 与 R。

时间不多，Hineven 想让这只高爆螺旋狗至少炸飞 K 只 cch 克隆体,你需要尽快求出最小的 X，这直接决定了他会喂这只狗多少火药并且达到如何的杀伤效果。

一句话题意：给出两个全小写字母组成的正方形矩阵A和B和整数K，A与B的边长分别为 N 和 M，要求出最小的 X 使得有一种方案来从 A 中挖出一个 X*X 的‘子图片’让属性值在长度为 X 的区间内的 B 在‘子图片’中出现至少 K 次。

输入格式

第一行输入 N，M，K，让输入行数为 i 接下来 N 行，每行一个连续的小写长度为 N 的字符串表示矩阵 A 的第 i-1 行

接下来N 行，每行N 个用单个空格分开的整数表示能出现在i-(N+1)行的对应位置的cch克隆体的战斗力

接下来 M 行，每行一个连续的小写长度为 M 的字符串表示矩阵 B 的第 i-(N*2+1)行

输出格式

第一行输出一个整数，你的答案 X，如果你想告诉 Hineven 打败资本主义只是一个梦想(无解)，输出-1。

样例数据

样例输入	样例输出
3 2 2 chh cch occ 0 9 0 0 1 8 0 0 0 ch cc	3

<样例解释>

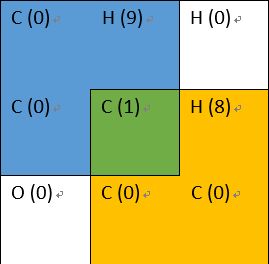
圈出 A 中(1,1)到(3,3)的 3*3 的正方形矩阵可以达到两次‘出现’出现的两只 cch的战斗力分别为 0 和 1，选择[0,2]长度为 X 的区间可以全部包含在内。

<数据范围>

对于 10%的数据 N，M<=10

对于 30%的数据 N, M<=60 对于另 30%的数据 N<=600，M<=100

对于 100%的数据 1<=M<=N<=600, 0<=K<=10^7, -100<=Cij<=100，且数据较为随机化

解析

首先发现这道题肯定和字符串匹配有关，把 B 的每一行作为模式串和 A 的每一行进行匹配，用 KMP 跑 M*(N-M)次匹配能算出所有 B 在 A 中出现的位置

时间复杂度 O((N-M)*M*(N+M))，另外JeremyGuo提供了理论上更快的O(N^2) Hash算法,将在Code部分里额外附上。

然后发现 X 和出现数量成正比关系，考虑二分答案，把 A 中的横座标，纵座标，以及每只 cch 的‘战斗力’分别作为第一，第二，第三个维度进行三维前缀和，二分 X 后暴力枚举立方体左上角进行判定。时间复杂度 O(N^2*max{Cij}*logN)

总时间复杂度为 O((N-M)*M*(N+M) + N^2*max{Cij}*logN)

Code

#include <cstdio>

#include <cstring>

#include <cstdlib>

#include <algorithm>

#include <cmath>

typedef long long LL;

const int MAXN = ;

const int MAXT = ;

using std :: min;

using std :: max;

char A[MAXN][MAXN], B[MAXN][MAXN];

int n, m, K;

int nxt[MAXN];

void getNext (char * str, int len) {

    int j = , k = -;

    nxt[] = -;

    while(j < len)

        if(k == - || str[j] == str[k])

            nxt[++j] = ++k;

        else k = nxt[k];

}

bool match[MAXN];

void doKMP (char * s1, char * s2, int l1, int l2) {

    memset(match, , sizeof match);

    if(l1 < l2) return ;

    int i, j;

    for(i = , j = ; i<l1; i++, j++) {

        if(j == l2) {match[i-l2] = true; i--; j = nxt[j]-;}

        else while(j != - && s1[i] != s2[j]) j = nxt[j];

    }

    if(j == l2) match[l1 - l2] = true;

}

bool tmp[MAXN][MAXN];

int pref[MAXN][MAXN][];

int attr[MAXN][MAXN];

bool check(int val) {

    int r = val;

    val -= m-;

    for(int i = r; i<=n; i++)

        for(int j = r; j<=n; j++)

            for(int k = min(MAXT, r); k<=MAXT; k++) {

                int t = max(, k-r);

                if(pref[i][j][k] - pref[i-val][j][k] - pref[i][j-val][k] - pref[i][j][t]

                   + pref[i-val][j-val][k] + pref[i-val][j][t] + pref[i][j-val][t]

                   - pref[i-val][j-val][t] >= K) return true;

            }

    return false;

}

inline int getInt() {

    int ret = ;

    char ch; bool f = false;

    while((ch = getchar()) < '' || ch > '') f |= (ch == '-');

    do {ret *= ; ret += ch - '';}

    while((ch = getchar()) >= '' && ch <= '');

    return f ? -ret : ret;

}

int main () {

    freopen("hedog.in","r",stdin);

    freopen("hedog.out","w",stdout);

    scanf("%d%d%d", &n, &m, &K);

    if(K == ) {puts("");return ;}

    for(int i = ; i<=n; i++)

            scanf("%s", A[i]+);

    for(int i = ; i<=n; i++)

        for(int j = ; j<=n; j++)

            attr[i][j] = getInt();

    for(int i = ; i<=m; i++)

        scanf("%s", B[i]+);

    memset(tmp, 0xff, sizeof tmp);

    for(int j = ; j<=m; j++) {

        getNext(B[j]+, m);

        for(int i = j; i<=n-(m-j); i++) {

            doKMP(A[i]+, B[j]+, n, m);

            for(int k = ; k<n; k++)

                tmp[i-j][k] &= match[k];

        }

    }

    for(int i = m; i<=n; i++)

        for(int j = m; j<=n; j++) {

            if(tmp[i-m][j-m]) pref[i][j][attr[i-m+][j-m+]+] = ;

            for(int k = ; k<=MAXT; k++)

                pref[i][j][k] += pref[i-][j][k] + pref[i][j-][k] + pref[i][j][k-]

                - pref[i-][j-][k] - pref[i-][j][k-] - pref[i][j-][k-]

                + pref[i-][j-][k-];

        }

    int l = m, r = n, ans = n+;

    while(l < r) {

        int mid = (l+r)>>;

        if(check(mid)) r = mid, ans = min(ans, mid);

        else l = mid + ;

    }

    if(ans == n+) ans = -;

    printf("%d\n", ans);

}

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <iostream>

using namespace std;

const int MAXN = ;

const int MAXT = ;

const int MOD_ROW = ;

const int MOD_COL = ;

const int MOD = ;

const int INF = 0x3f3f3f3f;

char A[MAXN+][MAXN+], B[MAXN+][MAXN+];

int n, m, height[MAXN+][MAXN+];

pair<int,int> poss[MAXN*MAXN+];

int sum[MAXN+][MAXN+][MAXT+], K;

namespace Hash{

    int hs[MAXN+][MAXN+], row[MAXN+][MAXN+], pow_row[MAXN+], pow_col[MAXN+];

    void Init(){

        pow_col[] = pow_row[] = ;

        for(int i=;i<=n;i++){

            pow_col[i] = 1ll * pow_col[i-] * MOD_COL % MOD;

            pow_row[i] = 1ll * pow_row[i-] * MOD_ROW % MOD;

        }

        for(int i=;i<=n;i++)

            for(int j=;j<=n;j++)

                row[i][j] = (1ll*row[i][j-]*MOD_ROW+A[i][j]-'a'+)%MOD;

        for(int i=;i<=n;i++)

            for(int j=;j<=n;j++)

                hs[i][j] = (1ll*hs[i-][j]*MOD_COL+row[i][j])%MOD;

    }

    int GetHash(int x1, int y1, int x2, int y2){

        int len_row = y2-y1+;

        int len_col = x2-x1+;

        int ret = ((hs[x2][y2]-1ll*hs[x1-][y2]*pow_col[len_col]%MOD)%MOD+MOD)%MOD;

        int tmp = ((hs[x2][y1-]-1ll*hs[x1-][y1-]*pow_col[len_col]%MOD)%MOD+MOD)%MOD;

        return ((ret-1ll*tmp*pow_row[len_row]%MOD)%MOD+MOD)%MOD;

    }

    int GetB(){

        int ret = , tmp;

        for(int i=;i<=m;i++){

            tmp = ;

            for(int j=;j<=m;j++)

                tmp = (1ll*tmp*MOD_ROW+B[i][j]-'a'+)%MOD;

            ret = (1ll*ret*MOD_COL+tmp)%MOD;

        }

        return ret;

    }

}

template<class T>

void Read(T& x){

    char ch;

    int f = ;

    while(ch=getchar(), ch<''||ch>'')

        if(ch == '-') f = -f;

    x = ch-'';

    while(ch=getchar(), ch>=''&&ch<='')

        x = x*+ch-'';

    ungetc(ch, stdin);

    x *= f;

}

bool check(int x1, int y1, int x2, int y2, int val){

    //if(x2 <= 0 || y2 <= 0) return false;

    for(int i=;i<=MAXT;i++){

        int l=max(, i-val);

        int sum1 = sum[x2][y2][i] - sum[x1-][y2][i] - sum[x2][y1-][i] + sum[x1-][y1-][i];

        int sum2 = sum[x2][y2][l] - sum[x1-][y2][l] - sum[x2][y1-][l] + sum[x1-][y1-][l];

        if(sum1 - sum2 >= K)

            return true;

    }

    return false;

}

int GetRand(int l, int r){

    return rand()%(r-l+)+l;

}

int main(){

    srand(MOD);

    freopen("hedog.in", "r", stdin);

    freopen("hedog.out", "w", stdout);

    int vis;

    Read(n); Read(m); Read(K);

    if(!K){

        printf("0\n");

        return ;

    }

    for(int i=;i<=n;i++)

        scanf("%s", A[i]+);

    for(int i=;i<=n;i++)

        for(int j=;j<=n;j++){

            Read(height[i][j]);

            height[i][j] += ;

        }

    for(int i=;i<=m;i++)

        scanf("%s", B[i]+);

    int hb = Hash::GetB();

    Hash::Init();

    for(int i=;i<=n;i++){

        if(i+m->n) break;

        for(int j=;j<=n;j++){

            if(j+m->n) break;

            vis = int(Hash::GetHash(i, j, i+m-, j+m-) == hb);

            //printf("1");

            for(int k=;k<=MAXT;k++){

                sum[i][j][k] = sum[i-][j][k]+sum[i][j-][k]-sum[i-][j-][k];

                if(vis && height[i][j] <= k)

                    sum[i][j][k]++;

            }

        }

        //puts("");

    }

    int pcnt = ;

    for(int i=;i<=n;i++){

        if(i+m- > n) break;

        for(int j=;j<=n;j++){

            if(j+m- > n) break;

            poss[++pcnt] = make_pair(i, j);

        }

    }

    for(int i=;i<=pcnt;i++)

        swap(poss[i], poss[GetRand(, i)]);

    int x=-;

    for(int p=;p<=pcnt;p++){

        int i = poss[p].first, j = poss[p].second;

        int L=m, R=min(n-i+, n-j+);

        R = min(R, (x==-?INF:x-));

        if(L <= R && !check(i, j, i+R-m, j+R-m, R)) continue;

        while(L <= R){

            int mid = (L+R)>>;

            if(check(i, j, i+mid-m, j+mid-m, mid)){

                x = mid;

                R = mid-;

            }else L = mid+;

        }

    }

    printf("%d\n", x);

    return ;

}

JeremyGuo Edition

毁灭计划

题目描述

资本主义cch在战场上建立了N个圆形堡垒,为此Ender作为一个熊孩子,想到了两个疯狂的毁灭计划,并将其命名为A计划和B计划。有了这两个计划,资本主义cch的阴谋就不会得逞。

A计划:压缩计划

压缩机产生的压强是非常恐怖的,于是乎Ender打算拆掉全世界所有的压缩机提炼出许多压缩核心并将其放置在圆形堡垒群外,形成一个封闭曲线,当所有的压缩核心开始运作,它们就会把堡垒压个粉碎。

B计划:铁板计划

这个计划非常的简单粗暴,Ender打算造一个巨型铁板,从天上扔下来直接拍死资本主义cch的堡垒。并且由于某种原因,任意两个被铁板覆盖的点之间的线段必须被铁板覆盖。

当0_1把这两个计划提交到总部后,总部觉得这两个计划非常的邪恶,决定两者都执行。

但计划的消耗是巨大的,并且要0_1自掏腰包,0_1打算尽可能减小这个消耗,A计划的消耗为封闭曲线的长度,B计划消耗为铁板面积。请你来计算最小消耗。

一句话题意:给出N个圆,和M,求一个圆的凸包，询问凸包周长和凸包面积(一看就是一道版题)

输入格式

第一行输入 N。

接下来 N 行,每行三个整数x,y,r。分别表示堡垒i的圆形坐标是(x,y),半径是r。

输出格式

输出两行,第一行表示计划A的消耗,第二行表示计划B的消耗。

保留三位小数。

样例数据

样例输入	样例输出
3 4 2 2 3 7 1 8 5 1 3.2	23.983 38.499

<样例解释>

如图

<数据范围>

对于 20%的数据 N<=10

对于另30%的数据 N<=100

对于另20%的数据 N<=500

对于另30%的数据 N<=1000

对于 100%的数据 |x|,|y|<=10000,0<=r<=100,圆有可能退化为点，圆可能重叠。

解析

首先给出30分解法: 可以发现二进制枚举按得数量就行了，观察可以发现f(n)=phi(n) g(n)=n，呵呵。

根据30分的做法，我们可以发现phi(n)最多向下递归Log（n）层就变成了1，呵呵，然后我们可以观察发现每个门相当于一个条件，表示控制它的两个开关是否同时按下。然后利用并查集或者二分图染色，检查是否可行就行了。

Code

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

#include<cstdlib>

#include<iostream>

#include<ctime>

#include<climits>

#include<stack>

#include<queue>

#include<vector>

#include<map>

#include<set>

typedef long long int LL;

typedef unsigned long long ULL;

const int INF=0x3f3f3f3f;

LL getint(){

    LL ans=;int f=;char c;

    while((c=getchar())<''||c>'')if(c=='-')f=-f;

    while(c>=''&&c<=''){ans=ans*+c-'';c=getchar();}

    return ans*f;

}

using namespace std;

//from here

const double eps=1e-,PI=3.14159265358979323846264338328;

bool equal(double a,double b){return a<=b+eps&&a>=b-eps;}

int sign(double a){

    if(a>eps)return ;

    if(a<-eps)return -;

    return ;

}

bool big(double a,double b){return a>b+eps;}

bool small(double a,double b){return a<b-eps;}

struct point{

    double x,y;

    point(){}

    int read(){return scanf("%lf%lf",&x,&y);}

    point(double _x,double _y){x=_x;y=_y;}

    point operator-()const{return point(-x,-y);}

    point operator+(point r)const{return point(x+r.x,y+r.y);}

    point operator-(point r)const{return point(x-r.x,y-r.y);}

    point operator*(double a)const{return point(x*a,y*a);}

    point operator/(double a)const{return point(x/a,y/a);}

    double operator*(point r)const{return x*r.x+y*r.y;}

    double operator^(point r)const{return x*r.y-y*r.x;}

    double length()const{return sqrt(x*x+y*y);}

    bool operator==(point r)const{return equal(x,r.x)&&equal(y,r.y);}

    point unit()const{return *this/length();}

    double atan(){return atan2(y,x);}

};

struct Round{

    point c;double r;

    void read(){c.read();scanf("%lf",&r);}

    point find(double a)const{return c+point(r*cos(a),r*sin(a));}

    vector<point> cutrd(const Round &B)const{

        vector<point>ret;

        point C=B.c;double R=B.r;

        point bar=C-c;

        double d=bar.length();

        if(small(d,abs(R-r)))

            return ret;

        else if(equal(d,abs(R-r))){

            if(equal(R,r))return ret;

            point pos;

            if(big(R,r))

                pos=find((-bar).atan());

            else

                pos=find(bar.atan());

            ret.push_back(pos);

            return ret;

        }

        double aph=asin((R-r)/d),bet=bar.atan();

        aph+=PI/;

        ret.push_back(find(bet+aph));

        ret.push_back(find(bet-aph));

        return ret;

    }

    bool in(const Round &B)const{

        return !big(r,B.r)&&!big((c-B.c).length(),abs(B.r-r));

    }

};

struct data{

    point c;

    int b;

    data(){}

    data(point _c,int _b){c=_c;b=_b;}

    bool operator<(const data &r)const{

        return equal(c.x,r.c.x)?small(c.y,r.c.y):small(c.x,r.c.x);

    }

};

//to here

const int MAXN=;

Round s[MAXN+];

data p[*MAXN*MAXN+];

data ans[*MAXN*MAXN+];

bool used[*MAXN+];

int main(){

    freopen("destroy.in","r",stdin);

    freopen("destroy.out","w",stdout);    

    int n=getint();

    for(int i=;i<=n;++i)

        s[i].read();

    int num=,cnt=,tmp=,buf=;

    for(int i=;i<=n;++i)if(!used[i])

        for(int j=;j<=n;++j)if(i!=j&&!used[j])

            if(s[j].in(s[i]))used[j]=;

    for(int i=;i<=n;++i)

        if(!used[i]){

            ++tmp;

            buf=i;

        }

    if(tmp==){

        printf("%.3lf\n",*PI*s[buf].r);

        printf("%.3lf\n",PI*s[buf].r*s[buf].r);

        return ;

    }

    for(int i=;i<=n;++i)if(!used[i])

        for(int j=;j<=n;++j)if(!used[j]){

            vector<point>ret=s[i].cutrd(s[j]);

            for(int t=;t<ret.size();++t)

                p[++num]=data(ret[t],i);

        }

    sort(p+,p+num+);

    tmp=;

    for(int i=;i<=num;++i){

        while(i<num&&p[i].c==p[i+].c)

            ++i;

        p[++tmp]=p[i];

    }

    num=tmp;

    ans[++cnt]=p[];

    ans[++cnt]=p[];

    for(int i=;i<=num;++i){

        while(cnt>&&sign((p[i].c-ans[cnt].c)^(ans[cnt].c-ans[cnt-].c))>=)

            --cnt;

        ans[++cnt]=p[i];

    }

    tmp=cnt;

    ans[++cnt]=p[num-];

    for(int i=num-;i>=;--i){

        while(cnt>tmp&&sign((p[i].c-ans[cnt].c)^(ans[cnt].c-ans[cnt-].c))>=)

            --cnt;

        ans[++cnt]=p[i];

    }

    ans[]=ans[cnt-];

    ans[cnt+]=ans[];

    double op=,ed=;

    for(int i=;i<cnt;++i){

        ed+=ans[i].c^ans[i+].c;

        if(ans[i].b==ans[i+].b){

            int r=s[ans[i].b].r;

            double aph=(ans[i].c-ans[i-].c).atan();

            double bet=(ans[i+].c-ans[i+].c).atan();

            bet-=aph;

            if(big(bet,*PI))bet-=*PI;

            if(small(bet,))bet+=*PI;

            op+=bet*r;

            ed-=r*r*sin(bet);

            ed+=r*r*bet;

        }

        else

            op+=(ans[i].c-ans[i+].c).length();

    }

    printf("%.3lf\n%.3lf\n",op,ed/);

}

Time: 2017-10-30