[NOI 2016]区间

Description

在数轴上有 $n$ 个闭区间 $[l_1,r_1],[l_2,r_2],...,[l_n,r_n]$。现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$，使得对于每一个被选中的区间 $[l_i,r_i]$，都有 $l_i \le x \le r_i$。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 $[l_i,r_i]$ 的长度定义为 $r_i-l_i$，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $−1$。

Input

第一行包含两个正整数 $n,m$，用空格隔开，意义如上文所述。保证 $1 \le m \le n$。

接下来 $n$ 行，每行表示一个区间，包含用空格隔开的两个整数 $l_i$ 和 $r_i$ 为该区间的左右端点。

Output

只有一行，包含一个正整数，即最小花费。

Sample Input

6 3
3 5
1 2
3 4
2 2
1 5
1 4

Sample Output

2

Sample Explanation

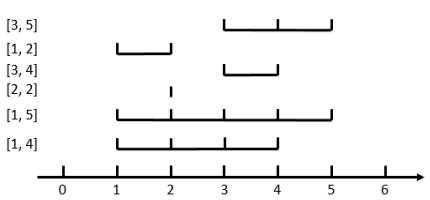
如图，当 $n=6,~m=3$ 时，花费最小的方案是选取 $[3,5]$、$[3,4]$、$[1,4]$ 这三个区间，他们共同包含了 $4$ 这个位置，所以是合法的。其中最长的区间是 $[1,4]$，最短的区间是 $[3,4]$，所以它的花费是 $(4−1)−(4−3)=2$。

Hint

所有测试数据的范围和特点如下表所示：

测试点编号	$n$	$m$	$l_i,r_i$
1	$20$	$9$	$0 \le l_i \le r_i \le 100$
2		$10$
3	$199$	$3$	$0 \le l_i \le r_i \le 100000$
4	$200$
5	$1000$	$2$
6	$2000$
7	$199$	$60$	$0 \le l_i \le r_i \le 5000$
8	$200$	$50$
9			$0 \le l_i \le r_i \le 10^9$
10	$1999$	$500$	$0 \le l_i \le r_i \le 5000$
11	$2000$	$400$
12		$500$	$0 \le l_i \le r_i \le 10^9$
13	$30000$	$2000$	$0 \le l_i \le r_i \le 100000$
14	$40000$	$1000$
15	$50000$	$15000$
16	$100000$	$20000$
17	$200000$		$0 \le l_i \le r_i \le 10^9$
18	$300000$	$50000$
19	$400000$	$90000$
20	$500000$	$200000$

时间限制：$3\texttt{s}$

空间限制：$256\texttt{MB}$

题解（转载）

->原文地址<-

首先发现那一个相交的点一定可以是区间的某个端点，所以可以离散左右端点，那么问题就简单了，然后仔细推敲，发现可以按区间长度排序，然后不就是尺取法了么?如果有一个点被覆盖的次数$>=m$我们就移动右指针，不然我们就一直往后走，对于覆盖次数$>=m$我们就维护线段树区间最大值，然后区间修改维护指针移动即可。

 //It is made by Awson on 2017.10.17
 #include <set>
 #include <map>
 #include <cmath>
 #include <ctime>
 #include <cmath>
 #include <stack>
 #include <queue>
 #include <vector>
 #include <string>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #define LL long long
 #define Min(a, b) ((a) < (b) ? (a) : (b))
 #define Max(a, b) ((a) > (b) ? (a) : (b))
 #define sqr(x) ((x)*(x))
 #define Lr(x) (x<<1)
 #define Rr(x) (x<<1|1)
 using namespace std;
 const int N = ;

 int n, m, ans = 2e9;
 struct tt {
   int l, r, val;
   bool operator < (const tt &b) const{
     return val < b.val;
   }
 }a[N+];
 struct ss {
   int val, id, op;
   bool operator < (const ss &b) const{
     return val < b.val;
   }
 }b[(N<<)+];
 struct segment {
   int sgm[(N<<)+], lazy[(N<<)+];
   void pushdown(int o) {
     sgm[Lr(o)] += lazy[o], sgm[Rr(o)] += lazy[o];
     lazy[Lr(o)] += lazy[o], lazy[Rr(o)] += lazy[o];
     lazy[o] = ;
   }
   void update(int o, int l, int r, int a, int b, int key) {
     if (a <= l && r <= b) {
       sgm[o] += key, lazy[o] += key;
       return;
     }
     pushdown(o);
     int mid = (l+r)>>;
     if (a <= mid) update(Lr(o), l, mid, a, b, key);
     if (b > mid) update(Rr(o), mid+, r, a, b, key);
     sgm[o] = Max(sgm[Lr(o)], sgm[Rr(o)]);
   }
 }T;

 void work() {
   scanf("%d%d", &n, &m);
   for (int i = ; i <= n; i++) scanf("%d%d", &a[i].l, &a[i].r), a[i].val = a[i].r-a[i].l;
   sort(a+, a+n+);
   for (int i = ; i <= n; i++) {
     b[(i<<)-].val = a[i].l, b[(i<<)-].id = i; b[i<<].val = a[i].r, b[i<<].id = i;
   }
   sort(b+, b+*n+); b[].val = -;
   for (int i = ; i <= (n<<); i++) b[i].op = b[i-].op+(b[i].val != b[i-].val);
   for (int i = ; i <= (n<<); i++) {
     if (b[i].val == a[b[i].id].l) a[b[i].id].l = b[i].op;
     if (b[i].val == a[b[i].id].r) a[b[i].id].r = b[i].op;
   }
   int tol = b[n<<].op, r = ;
   for (int i = ; i <= n; i++) {
     while (r < n && T.sgm[] < m) {
       r++; T.update(, , tol, a[r].l, a[r].r, );
     }
     if (T.sgm[] >= m) ans = Min(ans, a[r].val-a[i].val);
     else break;
     T.update(, , tol, a[i].l, a[i].r, -);
   }
   printf("%d\n", ans == 2e9 ? - : ans);
 }
 int main() {
   work();
   return ;
 }