机器学习实战 之 KNN算法

现在 机器学习 这么火，小编也忍不住想学习一把。注意，小编是零基础哦。

所以，第一步，推荐买一本机器学习的书，我选的是Peter harrigton 的《机器学习实战》。这本书是基于python 2.7的，但是我安装的是python 3.6.2.

所以很关键的是，你必须得有一定的python基础。这里我推荐runoob的py3教程，通俗易懂。http://www.runoob.com/python3/python3-tutorial.html

注意：python2和python3是不兼容的

python是面向对象的，面向对象是python的精髓。

————————————————————严肃的分割线......——————————————————————————————

         言归正传，首先，我们要安装一些包，比如numpy和matplotlib。小编推荐用anaconda，这是一个开源的Python发行版本，其包含了conda、Python等180多个科学包及其依赖项。下载地址https://www.anaconda.com/download/。这就免去安装各种包的烦恼。

　　界面如下：里面有一个spyder,这是一款很好用的IDE

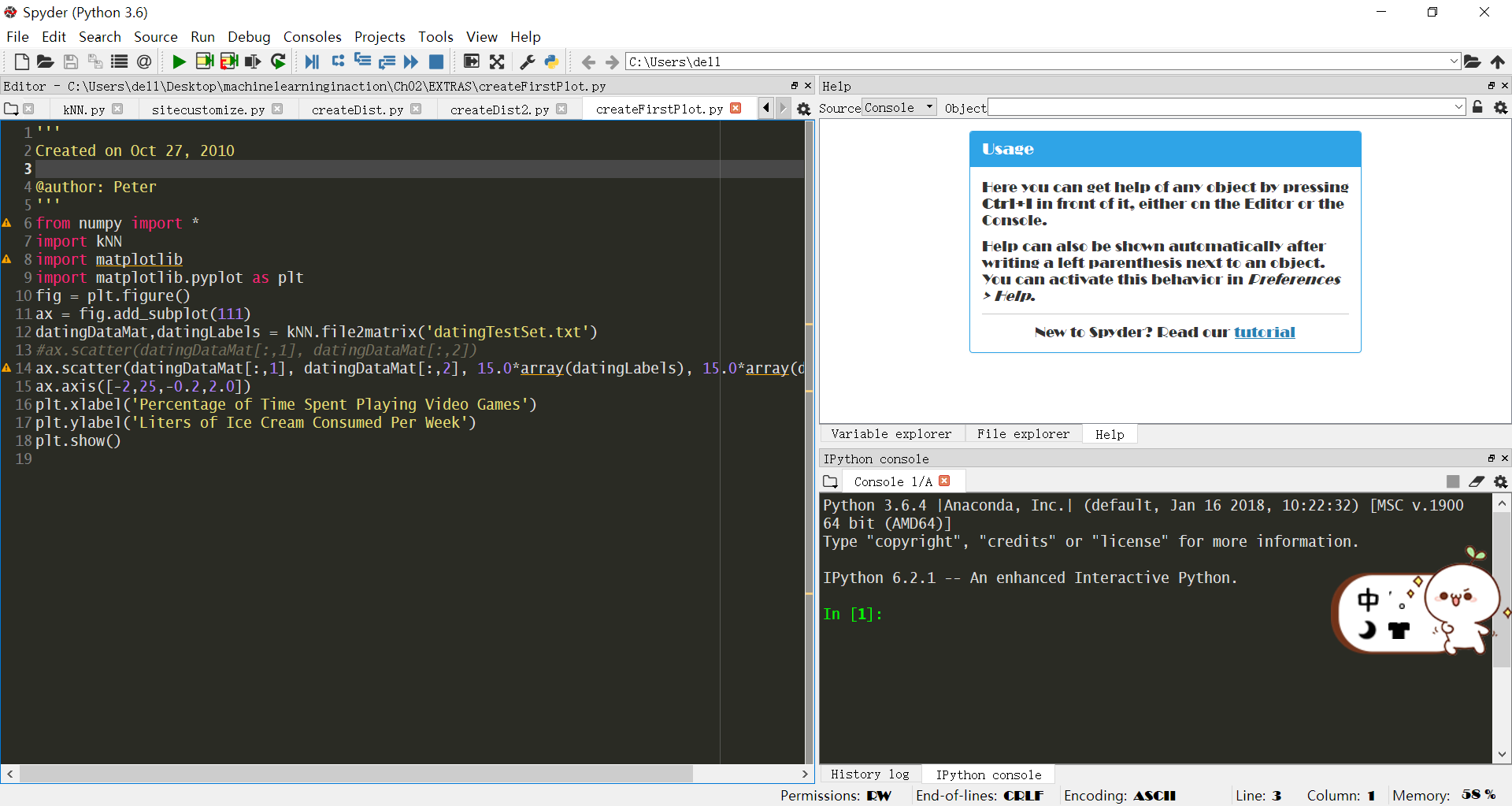
左边是文本编辑区，右下角是命令行。右上角是变量区，很方便啊，有木有！

下面就是KNN算法的讲解了。

————————————————————————分割线————————————————————————————————————————————————————

        K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理，但在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成反比。

　　

实例:手写识别>

      目录下解压digits.zip,得到训练样集本和测试样集本。kNN.py是核心程序。随便点开一个0_0.txt文件，可以看到

00000000000001111000000000000000
00000000000011111110000000000000
00000000001111111111000000000000
00000001111111111111100000000000
00000001111111011111100000000000
00000011111110000011110000000000
00000011111110000000111000000000
00000011111110000000111100000000
00000011111110000000011100000000
00000011111110000000011100000000
00000011111100000000011110000000
00000011111100000000001110000000
00000011111100000000001110000000
00000001111110000000000111000000
00000001111110000000000111000000
00000001111110000000000111000000
00000001111110000000000111000000
00000011111110000000001111000000
00000011110110000000001111000000
00000011110000000000011110000000
00000001111000000000001111000000
00000001111000000000011111000000
00000001111000000000111110000000
00000001111000000001111100000000
00000000111000000111111000000000
00000000111100011111110000000000
00000000111111111111110000000000
00000000011111111111110000000000
00000000011111111111100000000000
00000000001111111110000000000000
00000000000111110000000000000000

这就是经过数字图像处理的手写字体了，格式是32x32。

　　核心函数如下：

#inX：用于分类的输入向量。即将对其进行分类。
#dataSet：训练样本集
#labels:标签向量
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]#得到训练样本集的行数，即有几个训练数据
    diffMat = tile(inX, (dataSetSize,1)) - dataSet #tile:numpy中的函数。tile将原来的一个数组，扩充成了dataSetSize个一样的数组。diffMat得到了目标与训练数值之间的差值。
    sqDiffMat = diffMat**2#差值的平方
    sqDistances = sqDiffMat.sum(axis=1)#对应列相乘，即距离和
    distances = sqDistances**0.5 #开根号 即距离
    sortedDistIndicies = distances.argsort()#升序排列
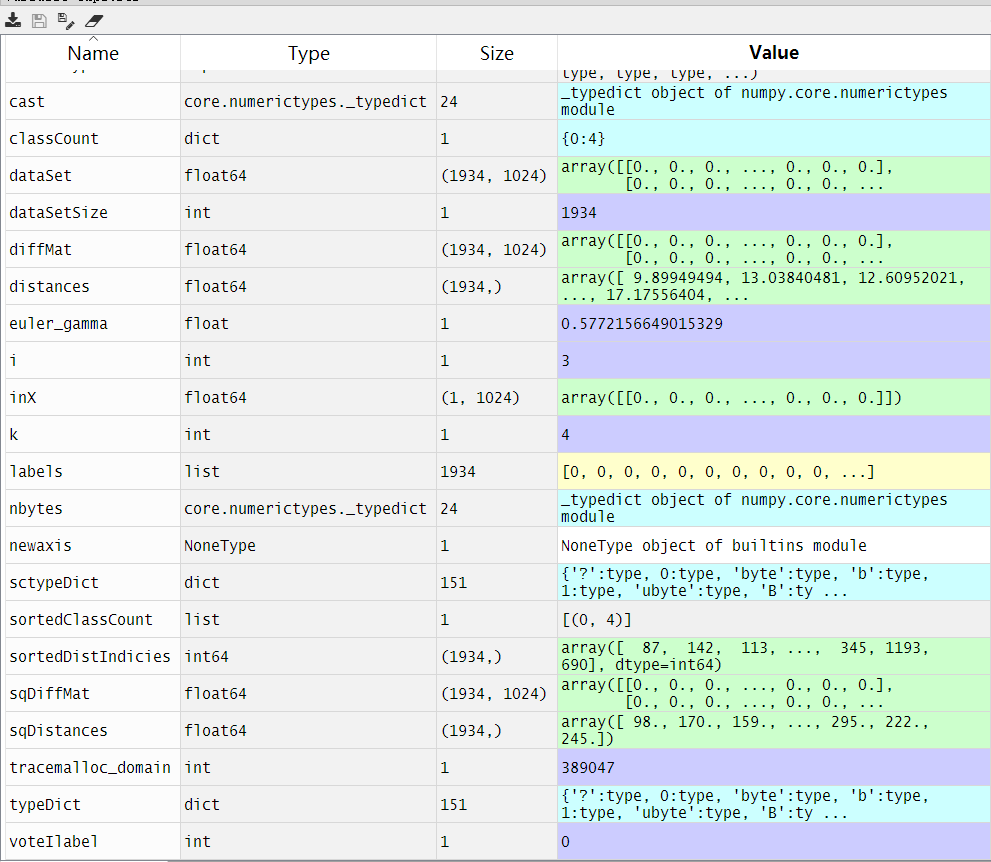
    classCount={}         #创建一个字典classCount  选择距离最小的k个点,
    for i in range(k):     #k次遍历
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #原书是iteritems() py3改为items()
    return sortedClassCount[0][0]
#计算完所有点后，数据按从小到大排序，然后确定前k个距离最小元素所在的主要分类，输入k总是正整数，最后，将classCount字典分解为元组列表，然后此处的排序为逆序，
返回发生频率最高的元素标签。

　　我们要知道的是在python中。classfiy0就是一个函数，而inX, dataSet, labels, k是输入参数，其中k就是KNN算法的K。

　　shape是numpy库中的函数。.shape用于计算array各维度的长度，在python中都是从0开始的。

　　tile 也是 numpy中的函数，它可以在行和列上重复一个矩阵。

aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAABIYAAAHCCAYAAACaHsLdAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAHUhSURBVHhe7b3bkyXJfd93/jK/OuSHjg5FWA/SeXA4wgpbZtimTCvI4YxDWrFttiySMWbM0AJBUeZQ5AybIJrkiACnl+TyMuw1gR7uisACJLho3HqxWOxisbgOgAXSeamsk5WV16o63afqfD4RH0yfysxfZVWd7u38our0SgAAAAAAAAAAwF5CMAQAAAAAAAAAsKcQDAEAAAAAAAAA7CkEQwAAAAAAAAAAewrBEAAAAAAAAADAnkIwBAAAAAAAAACwpxAMAQAAAAAAAADsKQRDAAAAAAAAAAB7CsEQAAAAAAAAAMCeQjAEAAAAAAAAALCnEAwBAAAAAAAAAOwpBEMAAAAAAAAAAHsKwRAAAAAAAAAAwJ5CMAQAAAAAAAAAsKcQDAEAAAAAAAAA7CkEQwAAAAAAAAAAe8rkwdCXr/4eERERERERERFnIMEQIiIiIiIiIuKeSjBU6Y994cdanz9/joiIiIiIiIg4WwmGKiUYQkRERERERMSlSDBUKcEQIiIiIiIiIi5FgqFKCYYQERERERERcSkSDFVKMISIiIiIiIiIS5FgqFKCof3wc+98X3zsi++LV994X/ztW++Lz33tffHJN98Xn/rK94P9EREREREREecowVClBEPj/Na3vyte/ezb4hXpJ7/wrvjMG++Jz33lm+Lzb31TvP7l98SnvviuePXybd1H9Q3VuA5f/vwPxK+/+iPxF18Q4q+/LMSn3xbiyetCPHz1ezc+N0RERERERMSpJBiqlGBonF/52rfET/zaK+LWb35C/PwfvC7+w599UXz442+K33/2pnj4l18Uv/TkdfGvTl4TP/WbnxRvvfutYI1t+V3pu9/6nvYvLr8v/uBv3xffe1+Ib39fiPd/KMTHr4T4+Zfek/P7pHj9y18nHEJERERERMTZSzBU6dhg6PKVl8RLL1lfEZeBPtN4KV7Z6j5s/cZXLgN9+n7la98U//xXL8TvPvuqeO0rPxCvv/2++NLX3xdvfet98e633xfvfecH4pNvfl/8+49/X3ztm+Ea21IFQief+JH47U/+SDz+ux+Jly6F+PgbQjz8hBCf/7oQH/uSEL//6R+KL779HR0OqTuHQnUQERERERER5yLBUKXTBENThzU2pHlZvPaWv22b4ZOy2U9hMPTm174p/qcP/pW48+gT4hc+cinu//Eb4lf+/C3xq3/xlvjgn74hfunsUvzbx6+L/+PxF8RXv/6dYI1tqYKo//DsfXHxxo/Em98S4u3vyPfzN4X4tVeEuPdHb4if+8Mvif/ryZviF/7T34n/8YMX4uhDnxRPP/WVYC1ERERERETEOUgwVCnBkG9lMPTON8Q/+3/+Uvzz//hp8S9/70r8zEfeEv/nk3e06mu17Sd+8+/Ej//qx/XdRaEa21IFQ7/ysefi9Xd+KH74I6H95veEePCqECcff0f84h9eip85fV2cvHylPfrdz4o/eIVgCBEREREREecrwVCl2wmGNsHOyy+rf40vv/aWM2bzWnv5iun3ymviNWeM2aZCmk0w9NprL7dtnRpvvSZetmO04WApOt7tVxgMffmdb4j/7hf/VPzvv/sl8X8/fS5+8S+/11FtU22qj+obqrEt3/nGc/Hvzr8t/u6r74vvvy+0X//uj8QH/+q5+ONPf0P88h99VvzrD31KfOyz74mvfuuH4tde/pp48bV3g7UQERERERER5yDBUKXbDoZMMPNWE/Y0r22A8/Jr4q1OHdvfH+9us2HOJugx+y59HRtvbbaXBkNvvyf+m59/Ufzkb31W/NxL39RBkKvaptpUH9U3VGNbvvON74p7f/Z18dqb3xff+YHQqgDo/ktfFT/9W58WP/HgVfHj/+8r4l/8x0+I19/+vn4E7snfvBOshYiIiIiIiDgHCYYq3W4wtNnu3yXUCYJsUNSGMXZ8KBjyg56mT3vH0SbQsft85bJgfDOm3V4YDL3x1ffEPzn+iPhfHrwmjj76VXH84rsd1TbVpvqovqEa2/Lt974rfuGPvipe+dL3xDeeC+3XpV/+xg/Fl979gfji174vnr7+LfFv/vAr4jNvvy9+6U/eEB95xb+DChEREREREXE+EgxVet3BkAlppE2Qo4Kit5pHu9q2YGiTCXZuLBj6uvhHP/N74n/45Wfip377Uvz073y+o9qm2lQf1TdUY1u+/d53xL/56BviY5//rvjCO98Tn/zie+KvX/+qOP/kF8Wf/vXr4rUvvKPbfvajXxafeut98YtnXxSPn305WAsRERERERFxDhIMVXo9wVAohNk8XqY/h8h5rKz36FlRzVh77vW4YOjqra+Lf/gvPyT+23sv6zuDQqo21Uf1DdXYll/9+rfF0e9/XvzlZ78tPvfOD8Sn3vi2+JsvvCcu/v6r4v/79JfFp6++odv+9e99QXzizffFL3zkc+L3Pn4VrIWIiIiIiIg4BwmGKt1uMNR1c0dQo73LJ9Bm7yLS6pCmINgp/PDpaYOhd8XB7Udi/Qt/Jn7sV/+z+J9/7ZP6L5Qp1ddqm2pTfVTfUI1tqYKhf/U7fy/+7DPfEp/72vvi9a9+T/zdm98Rn7r6pvjEF94Tn/nKd3XbT5/8vfjI37wrXvidvxWnf/XFYC1ERERERETEOUgwVOl2gyF/u6cNhjp3C920dcHQl956V/xXP/kb4r/+2TPx3//yM/G//sbfitsf/oJW/Zn6f/Yrr4h/dPyi7qP6hmpsy7fe/Za4/Vuf1n+B7FNf/q742N+/I/78E1fiD//qM+L3/vwT4vzTb+q2H3/wSf3XyW79xt+IP7j4UrAWIiIiIiIi4hwkGKp0mmDI6t+NkwqG7ONigTuJbkQ758bSYOgrXxP/5f/2QPwXP/7r4h/c/h3xD48+Kv7xv/0T8U9+/k/FP/65P9Gh0D+4/WHdR/UN1diWKhj6qd/8hDh77T3x9+/8SHzm7R/qP13/t2/9QHz6K98Xn5Ffq7af/I1PiM9++T3d/71vfidYCxEREREREXEOEgxVOjYY2ne/8a1viz9/9bPiT559VvzZq58XTz/xJXH+2hvi5U+9Ic6lf/nalfjz//wF3Uf1DdXYll/52rfEv/j1V8XP/t5nxK/+6ZfEyV+9JR6/+o5Wfa22qTbVR/UN1UBERERERESckwRDlRIMLVd19496NOw/XVyJP/6bN8X5374tLj77rlZ9rbapNtWHO4UQERERERFxCRIMVUowhIiIiIiIiIhLkWCoUoIhRERERERERFyKBEOVEgwhIiIiIiIi4lIkGKqUYAgRERERERERlyLBUKUEQ4iIiIiIiIi4FAmGKiUYQkRERERERMSlSDBUKcEQIiIiIiIiIi5FgqFKCYYQERERERERcSkSDFVKMISIiIiIiIiIS5FgqFKCIURERERERERcigRDlRIMISIiIiIiIuJSJBiqlGAIEREREREREZciwVClBEOIiIiIiIiIuBQJhiolGEJERERERETEpUgwVCnBECIiIiIiIiIuRYKhSgmGEBEREREREXEpEgxVSjCEiIiIiIiIiEuRYKhSNxgCAAAAAAAAAJgzBEOVEgwBAAAAAAAAwFIgGKqUYAgAAAAAAAAAlgLBUKUEQwAAAAAAAACwFAiGKiUYAgAAAAAAAIClQDBUKcEQAAAAAAAAACwFgqFKCYYAAAAAAAAAYCnMNhg6u7cW63Xj7QfiWa/PU/Hotmq/K856bcNdRjD0KXH8T/+dWP3T3xanX2w2AQAAAAAAAMDeMctgSIdCbRjUBED3Hm/6PLkr1utb4tFD9S/BUJ/dDoYuHqi5/TtxfNFsAAAAAAAAAICtMMNg6LG4r0KfC2ebDYL0NtXehEF6+44FQxfHYrU6FtHMY2z7AiAYAgAAAAAAALge5hcM9cIe+8jYWtx/4vQL9h3v6GBIcnG8EqvVoTi9ajZ4jG1PYUMXY/eOId12fCaOj0374Udfbu4ssiFNc6fRg5fFadNn02Z5s9PW3YdtOxMX7V1L0gef0q1XH/1tZ5xr6Z1NV+L0cCXncyGOV+oc+efJtjcvFSpoOzyVLc3XstGcX9XP9N/UCNXf1Ls6PZSv/dDO9D0ccrEAAAAAAAAAtsw8gyH7GNnFA3FHB0ImHJpLMKQwIYIXUjiMbY+RDYY6gYyjDm+cMKejrZNrt8HQb4vDTnhkwqWpgiE3DNIhjw1+SoKhJsTZnF8zxgQ7tv6mRjcMMiFQtD4AAAAAAADAjjHbYOjs4S2xeXxsfsGQ5upUHDZBRJCx7QlMCBQOhlSwsWm3dwm5wdBmnB1z+NE35Ysz/bW9A0jRae/cTaTuGpKH0IRBpt3gzqOOTPCTa9fBkAl5dOCjt/eDoe68VBjkBVFtB3csAAAAAAAAwO4x00fJ/L9Epj5XaL7BUPQzg8a2J9gEP80GidlmAhv99fHL4sqGOW4wpLc3NGGQCnZsyNMNXjbtbjDUDVe6zC8Ycrbpa9JcD/drAAAAAAAAgB1kfsFQ+/iYvy0QAO1yMKRDCD9kcBjbnmGaYMgLeorvGOru12dWwZAOf/qfY6T6qxrcLQQAAAAAAAC7zPyCIWn2z9VbU8FQEzDVBkdTBENjP1w61x4n/RlAxcFQTzMm314WDPU/ayjdf0NZMNQ+6mXvuBoRDHUfHWvQ+zwWx4dDrhEAAAAAAADA9THLYMj9S2TaTijktbV6f+L+poIhJ3wIMrY9yRaCIfexMsUXXxaHnT42FFKUBUP9/UwVDEnax++U8jy67c65TQVDZmyjHwppmr9aFmwDAAAAAAAA2B1mGgzdnKODoVnTBDZ+GLQ3BIKnIIG/TgYAAAAAAACwgxAMVUowRDCUC3z042XuXUoAAAAAAAAAOwrBUKUEQwRDsWDIfPYToRAAAAAAAADMB4KhSvc7GAIAAAAAAACAJUEwVCnBEAAAAAAAAAAsBYKhSgmGAAAAAAAAAGApEAxV6gZDz58/R0REREREREScrQRDlRIMISIiIiIiIuJSJBiqlGAIEREREREREZciwVClBEOI07p6YRXcPtZc3TH7HTvnKcb7hvopU2375K6fhymu4XUdI+8pRERExGVJMFQpwRDitNYsMlXfkLG+oe2uJX18h4zxLa2h+oUM9Y0ZGh8yNHauho5n28fonktfv5/72jXWlhpjDe0npNunxNCYIXUQERERcXclGKqUYAg3nouj1YE4uexuvzw5EKuVXIRpj8S507Z91ZzsvqVH54E+Y1T1hx+Tu0AtNVYntN3V7ePWK9WvVaM7NmRJn5g1Y4fu5/JF+R5ujmX1wg28h9t9Sz807D3sH7v/emrd+rGv7evYXGq3W3PtY/Xrb3t/iIiIiHi9zjYYOru3Fut14+0H4lmn/bG4b9uU9x47beMkGJqDl+LkQC6+AgHGdKGN2cfByWWvTe8jEcicH9n9Sw9OxGWgT8rS8bpfZTDUPT9G/xhNn/i5U6HCwYtqjDxHH1iJo4twP+XQBWZsnLs9Vbt2vzX9S/qW9qnVH19Sxx1j1cFQIpA5/5BT4wMD3sOF43U/bx7d0Mpo3m/dsWq7/zqm22+obi33X7++36fEVF+3rabmRvN9mgoA/brqdUy3HyIiIiLOw1kGQzoUasOgp+LRbTf8Ma/vP7H9TUh05+HT5vU4CYZuXh1MJAOVeDDUen6Ubs+YmkMqGNJhTTuumWdFeFMzfnAwlB2T2a9czJswyCw4Y8FQaBFZurB0F6LumNjXvqm2kDX9S/rW7t+1tn6qf6wtFQzpsKYNc8w1rrmrp2Z8NBiq2J9yyDmo1dZR/1rd7X4/f5s7JtQe2u5b2q/1Qv4cfOFAnLyo/i37eZjaR/X+EREREXEnnGEwpIKeW+LRhbPtyV2x9rc5doOkcY4OhnKBxNj2PTAfDBU45jxenoiDwCNk1ni4Enj0TM8jXqtr3fjtBUPSxDnYBEPqkSDZ53P9PsrQIrJkYen3cV/HvvYt2Y+rXzdkqG9Mf6y1pq9raJw11N81NCYevgSuqQ0XIte5a934bQdDse1DdM+pb6w9VMPfltru6vax9WOafupaND8D9TUo+3m4GV+2HRERERF33/kFQzoEuivO2m3NHUNr9y6hrjsVDEn1gj0RBoxtj2vu9Dg6VwGDquHXse3OGBU82BBGfX103uxf9TP9NzVC9Tf1dOjQC2NM39AjWb5m/Kbuxs0xdPskFjqJYMgenzYQQOl9JIKpaLjS26c9f945j1k5Xh/HtoKhZt+d66YXl3KfQbvn2m5vxzrb/W2+fh/3dexrX9UWM9Y/9HVoW6yGa0kfq98399o31R5ri4YvvQBBvg/0Y0jyPZh4ZLC1cvwUwZB/jKnzMZWpfQxpy81ZtQ/dp7YwGPLrZOsiIiIi4iycZzBkQ56LB+KODoT8x8dcd/NRMhtgxAKBse1hbZCwCVJ0eOA9mtSp6QdDcp8qDNjs3w0IbP1NDdPPLjhMCBStX6iumRvTC1E8I+1+mNI9P5ttqSBLzy8WDNla+o6bzfkruo6V4wcHQ7Jua+I8h49TzucD8v2l7v74nJxjYLFpF5PuvzHdcf4Yf1vqa99YW8n2UJ9cu29JH6vqmzM0zhrq7xoakwyG7GNg+vrK996FuubqX69vyMrx0WDImX/sM4pixxbbPtbOnDz9fu5r11Cb3RYbl2tXptq0mWAot29EREREnLezDYbOHt5yHh+LBUP2biL3DqNxThUMaZvFfTRkGNveMxAidIKZTLsTpmzCGTPGDYa6IYUKg7wgqg0T3LHumLTbC4a6c9Xqc+xuy885Fwyd6/DF1gyds4iV44cEQ12bO78i5zp8HeQYu8B0Q4BGdyEZWlSmFpp+m3od2hb62jfWVrI91CfX7lvSx+r3zb0OWbM/ZS4YOtfhjHwP6se/5HuwMhgqHR8Khrqq95vsEwiHYsdcey6GmNpHbZvdlpv30H1qCYYQERER99qZPkrmPxpm7grygyHzl8vinz00xG0EQ9EAY2x7z0CI0IQNZlGVaXfClLpgyNmm59zM1/26wq0FQ+359J0wGFL1OnP3zk/KyvHjgyFp4jz610Ev4uVCMWTJX42KbUvp93dfx2ql9lEyRn0dMtQ3Zkkfq7uPmKFx1lB/19CY9KNkclwniDHhTHEwVDE+HwxJA6FG7Ljs9li7q55nQb+QdmyoRqqmbXP7hLaFLKkbNREMxcaWzgsRERERd9/5BUPt42P+tu5dQc86dxRN52TBULPIjwYCY9uD3kAwpMOWcLCiaqQClpjbDYbcuYZ0jzfUngiGmuCpf34S83StHD9FMKSPJVI/eJzO42O5z4IJLShrFpm5vrH21LghY3xL+tbU8y0dq/rZvv4Yty1k9Nq1j3/52wrfw5XjS4Ih82hZd3zs2GLnI2TuHPna/qlxdnuq3W3z+8XGKYe2aQmGEBEREffa+QVD0vSfqy8MhZqAqfYxsymCIb1gTwQQY9vjZoKfpr1d7DdBxJhgKBhO6H0eiaODyDHY/cYCEz2PzPGHgh/XYLt3/BFzwVQ0GJLq8xE7363mLqDQ/MvGO32DbfH6HZvrEA7B3OvubFcLzOZukG0GQyX9htSPtZfOSzl0biFVv1JD411r+qaunQ5r2jt+5PtAfXh0r6+5CygUNpSNd/qmgqEmaHLvSIsdn7+95DyU9KnR1hs6x9R8hrZpI8FQbFzNvBARERFx951lMOT+JTKtEwrZx8raNsf+XUZq+zUHQ4MCC8dce1KzmI8HQ9I2lFHK/bjtzr5TwZAZ25gKJiKBRjYYkppwzGpDosD+q9ojfdzzo2zm1zmPjqlgqFc/2G/Tp7+PkvHGeDAUr989r/FjNOcgEM45wZBa1IceIbOqxWSJoXH+tpB+v5JxsT6l+1SO2U+JtWNVf39MaJtrOtST7x8V5jQ1wv02ffqPiJWMN4aCIb3Njg3UV9vc17Ftqe3KVFtI2z/3r/91zFif2u3KcJt3HVrl97X+7KfwuNC21HZERERE3H1nGgzdnKODoUVrAodomNBqgqF8v921e+dO13QwVKaukbsrKmM8GBpb31zn1ON0JQ5ZSJaMUX2s7ja3j6/f3zc3XmlruH3dbaVOPdZuCxnrl7vbq0TziNcmZBhi9o6hAkvOQcm2nHZM7F/f1D5SbcpQe2yb1W8bYq7OVPtBRERExOuVYKhSgqGUZcFQKlSZj+ZYQ8HL+GCoqT3yHGXvGBpYXx/f7K8fphwfDMn3mLobpfMh0/VOEQwhIiIiImJagqFKCYZSpoOh9jGlxYQK6s6n/l035m6c5lhrH/vTj+vJcYODJfv5QY1+nUnqD32UEeeiudtHvk+0lddbf16NHDc40JHvsXbfY+ogIiIiImKJBEOVEgwhIiIiIiIi4lIkGKqUYAgRERERERERlyLBUKUEQ4iIiIiIiIi4FAmGKnWDIQAAAAAAAACAOUMwVCnBEAAAAAAAAAAsBYKhSgmGAAAAAAAAAGApEAxVSjAEAAAAAAAAAEuBYKhSgiEAAAAAAAAAWAoEQ5USDAEAAAAAAADAUiAYqnS/gqELcbw6FKdXzcuGq9NDsVqtGo9lLwDYDdT3rP3elB77352qne9ZAAAAAADYMNtg6OzeWqzXjbcfiGdO27OHtzZtynuPO2PHuD/B0JU4PVyJQz8VkuhgqLfg3HBx7CxMD09lpWmhfhrqp9mX+rpf4PvUBLuEQwAAAAAAYJhlMKRDoTYMeioe3U6FP4/F/fVa3H8Saqt3X4IhvXiMLDpTwZBejLbjTLiUCpFqoX4a6qfZp/q6b7Bt+nkBAAAAAMB8mWEwpIKeW+LRhbPtyV2x9re1muDozsOngbZ69yIYujoVh4FHyCzxYCjw6NnFsVglatVB/TTUT7Nf9ePBkCTzPQ4AAAAAAPvD/IIhHQLdFWfttuaOodhdQRcPxJ1oaFTvFMGQXrDZR0G8Rzra0EUv+Ewf93GuXLsiVl+P7T1CohabgX20dyX0iQZDek5u/ebOBFk/tj6tgvppqJ9mz+ong6FmbOhRUQAAAAAA2C/mGQzZx8h06KMCIRMOucGQ+xlEU90tpBwbDKlQxV2r6cWbE8KY8MbZ5v0/+yXt8fomBOqsFdVi0wuB1JjUgjEZDHXmpfZlFqDR9WkN1E9D/TR7Vj8dDKkSke9jAAAAAADYK2YbDJ3pD5i2dwL1g6GNuc8gqnNsMNTDXexJTPDj3hXQDXNy7T28+t3FollUdkOg0LYuuWDoQs/RhlXTL4ypH4H6afasflEwJOvpMgAAAAAAsLfM9FGytfeXyDIfMN17/Gy4o4Oh5v/p13f9WJ3FWe7/xc+15+qb9iZYcr9uMQvNwcGQv79ccFUD9dNQP82e1ScYAgAAAACAEuYXDLWPj/nbEsGP+/jZSMcFQ2YR1wld1GLPWZyNC4by9d3gR9XqB0AjgqH28ZbmtSIYPg2E+mmon2bP6vMoGQAAAAAAlDC/YEg65M/V9z5nqAmYau8kmjYYMq+3Fwz162t0WHQsjg/t4yhd9D4SdxKk5qAXo+1YEzL1+zbzGrBgpn4a6qfZj/oG3TfSZsemAmAAAAAAANgPZhkMuX+JTNsJhbw2afyvlan26wyG5HJMhSp6Uag8FKenU94xlK9vaBamsTqhOxMc0nNoFqt2DsF+mz6JQ4lA/TTUT7MP9Q3JYEh/j4eDYQAAAAAA2C9mGgzdnGODod3ABEOpRWn3zoQuuXCqBBNgbW9hSv001E8z9/qKeDBkwiXuFgIAAAAAAAXBUKVLCIZSoc+G5s6EwMJSL2pHBUNN7ewchkL9NNRPM/f6hlgwpL9/t7xvAAAAAACYDwRDlc45GNILRfX4SfGiUN1Z1L+rwdzt0NSq/ZwU+5eVRt5xFIX6aaifZu717WOi1t5+VHv9ZxsBAAAAAMByIRiqdM7BEAAAAAAAAACAC8FQpQRDAAAAAAAAALAUCIYqJRgCAAAAAAAAgKVAMFSpGww9f/4cEREREREREXG2EgxVSjCEiIiIiIiIiEuRYKhSgiFEREREREREXIoEQ5USDCEuy9ULq+D2sebqjtnv2DlPMd431E+Zatsnr/M8XNe+uLaIiIiIy5BgqFKCIcRlWbO4VX1DxvqGtruW9PEdMsa3tIbqFzLUN2ZofMjQ2LkaOp7rOkZ/P/b8+rp9SgyNGVIHEREREXdPgqFKCYZw47k4Wh2Ik8vu9suTA7FaycWX9kicO23bV83J7lt6dB7oU2r4+Lar2mfqnOXa07oL41JjdULbXd0+br1S/Vo1umNDlvSJWTN26H4uX5TfQ82xrF64ge+hdt/SDw37HvKP3X+9Dbe9j5s4JkRERETcvrMNhs7urcV63Xj7gXgW6PPlq6fi0W3V55Z4dBFqr5dgaA5eipMDuaALBAjThTZmHwcnl702vY9EIHN+ZPcvPTgRl4E+KUvH636Dg6H48aXOb5np8eYaxWtn2188EAcvqnnL/XxgJY4uwv2UQxe2sXHu9lTt2v3W9C/pW9qnVn98SR13jFUHQ4lA5vxDTo0PDPgeKhyv+wXnYd5bqdDKP7Z2fwHdfkN16wyruXvHhIiIiIjX4yyDIR0KtWFQE/7ce9zr9+zhLdnvlrhDMLQodTCQDFQKgovzoxHBRnoOqWBIhzXtuGaeFeFNzfgxwVD0+PR5OxAnJwPPX9H43HnJHLdczJswSPZLBEOhxWvpgtZdALtjYl/7ptpC1vQv6Vu7f9fa+qn+sbZUMKTDmjbMMde45q6emvHBYOhCvndfkO/hF9W/Zd8DQ87BGKtrzuCYEBEREXF7zjAYeizu+0HPk7uBu4Jsv0D/EY4OhnKBxNj2PTAfDBU45jxenoiDxCNW8WAo8GiWDUqKHteqGz84GIoen/MY16DzVzE+c45T7ZtgSD0SJPt8rt9HGVq8lixo/T7u69jXviX7cfXrhgz1jemPtdb0dQ2Ns4b6u4bGxIOhwDW1oUbkOnetG98PhtT45n2rx5V9D8SOM7Z9jG5Ne45jmn67f0yIiIiIuF3nFwzpEOiuOGu32cfF1uL+k00/fVeRvotox4IhqV6wJxa9Y9vjmjstjs7lQsA+itSpY9udMWoBb0MY9fXRebN/1c/039QI1d/U04FJLwwwfcOPLHU14zd1N26OodsnscBJBBP2+LSBACoXTEWDod4+7fnzznnMyvH6OAYEQ7nj0ybOX5HZ8ebY4u+LQLte1MpjDtrdl93ejnW2+9t8/T7u69jXvqotZqx/6OvQtlgN15I+Vr9v7rVvqj3WFg2GesGFfB/ox5/k90DikcHWyvHBO4ashSGKf4yp8zFWVTtVP7vvHTwmRERERNy+8wyG7GNkFw/EHR0ImXCoDYb0dhse7V4wpLQBRiwQGNse1gYJmyBFhwdtCGDaOzXVAt4NhuQ+1WJ8s393gW7rb2qYfnahYUKgaP1Cdc2xwUWk3Q9Tuudnsy0VZOn5xYIhW0vf8bI5f0XXsXL80GAod3za3PnNWTA+eh4bw+3yfHxAvr/V3R+fk+cosMi1i1j335juOH+Mvy31tW+srWR7qE+u3bekj1X1zRkaZw31dw2NSQZD9jEwfX3le/9CXXP1r9c3ZOX4McFQ7Nhi28dq66bqZ/e9Y8eEiIiIiNfjbIOhM/X5QW3g4wZD5us7D582Y3YzGNI2i/voInxse89AiOCGDUXBkFk0bMIZM8bMITBeh0FeENUu5t2x7pi02wuGunPV6nPsbsvPORcMnav2tmbonEWsHD8sGCq8Jrnzm7NgfO46h9vlNbQLWzcEaHQXsKHFbGqB67ep16Ftoa99Y20l20N9cu2+JX2sft/c65A1+1PmgqFz1d4+/iXfs5XBUOn4OQVD1lT97L4JhhARERH30pk+SuZ++LRShT9NMOTeUdS27XYwFF0gj23vGQgRmrDBLJ4z7c5ivi4YcrbpOTfzdb+ucGvBUHs+fScMhlS9ztwDd1HFrBy/b8GQXsTLBWpI81fKuuPV9pJtKf3+7utYrdQ+Ssaor0OG+sYs6WN19xEzNM4a6u8aGpN+lEyO6wR+KgyU3wOlwVDF+KHBUOy47PZYu6ueZ0E/39SYbL0tHxMiIiIi7qbzC4bax8f8bebRsc6fsfftBEbDnCwYahb50UBgbHvQTPCTa9f7NIuG4mBIhy3hYEXVyAYQAXOBgdaZa3F7b64h3eMNtTfzCwUyTfDUPz+JebpWjl9EMJSYf7DdeXws/gHGxtBCtmZxm+sba0+NGzLGt6RvTT3f0rGqn+3rj3HbQkavXfv4l7+t8L1YOZ5gaGNsrN0+ZK6IiIiIuBvOLxiSlv65emPkjqEmYOp+kHXeKYIhvWBPBBBj2+MGghu1QPeCoXax3QQRY4KhYDih93kkjg4ix2D3GwsO9Dwyx58LHoLt3vFHzAVTqUBDn4/Y+W41dwGF5l823ukbbIvXV+aOT5s8v+n62tz16byvKtrVwra5G2SbwVBJvyH1Y+2l81IOnVtI1a/U0HjXmr6pa6fDmvaOH/k+UB8e3etr7gIKhRxl452+lcFQ7Pj87SXnoaSPb2pMtt41HBMiIiIi7p6zDIbcv0SmjYZCyh0LhgYFFo7ZBXVKs5iOB0PSNpRRyv247c6+U8GQGduYCiYigUY2GJKacMxqQ6LA/qvaI338kKSZX+c8OqaCoV79YL9Nn/4+SsYb48FQqr40enyBc6P1Q7pY/dLxUj2HwPZcuxMMqUV96BEyq1rElhga528L6fcrGRfrU7pP5Zj9lFg7VvX3x4S2uaZDPfk+UmFOUyPcb9On/4hYyXhjPxjyxrbK92Lz5+7V603/+LbUdmWqLWV9zes7JkRERETcTWcaDN2co4OhRSsXGHLhHwtMNppgKN9vd+3eudM1HQyVqWukgpEC48FQvn7q+EocN3/zPqq+W6jSIQvYkjGqj9Xd5vbx9fv75sYrbQ23r7ut1KnH2m0hY/1yd3uVqGs44cYQk3cMFVpyDkq2lRqrZ/XbhpirM9V+EBEREfF6JBiqlGAoZVkwNDZ02A3NsYaCl/HBUFN75DnK3jGUrB8/vrzj5q/PX2Jsrh3n7/hgSL4H1V0wnQ+ZrneKYAgRERERcdclGKqUYCilCQRiwZAOKtSjQ4tZ1Ks7n/p3xZi7ZZpjrX3sTz+uJ8cNDpbs5/s0+nWq6oePL+kk80+ds1w7LkFzt498H2krr7f+nBw5bnCgI99j7b7H1EFEREREnIcEQ5USDCEiIiIiIiLiUiQYqpRgCBERERERERGXIsFQpQRDiIiIiIiIiLgUCYYqdYMhAAAAAAAAAIA5QzBUKcEQAAAAAAAAACwFgqFKCYYAAAAAAAAAYCkQDFVKMAQAAAAAAAAAS4FgqFKCIQAAAAAAAABYCgRDlRIMAQAAAAAAAMBSIBiqdL+CoQtxvDoUp1fNy4ar00OxWq0aj2WvLrn2m0Udk52b9NifXUn7rh0TAAAAAAAAwDBmGwyd3VuL9brx9gPxzGl79vDWpq3xzsOnnfFD3Z9g6EqcHq7EoZ8KSXTw0wtMNuTaL46d4OXwVO5pWkrr6365eQbaTfBFOAQAAAAAAADzZ5bBkA6F2jDoqXh0W76+97ht18GQ83pK9yUY0uFHJFQZEwzpsKWta8KnVK1aauoPDYa2MW8AAAAAAACAm2CGwdBjcX99Szy6cLY9uSvWzjaCoZFcnYrDwCNkluHBUODRtItjsUrsq466+sODIUnmHAEAAAAAAADMgfkFQzoEuivO2m3NHUPrtbj/xGzb9WBIBw72USfvkaQ2VNGBhunjPs6Va1fE6uuxvUegzGfq9PaReAQrHvwYou16zu7+mztv5P4T5cqprD8qGGpqhx61AwAAAAAAAJgL8wyG7GNkFw/EHR0ImXCoEww5ny/kfwbRGMcGQyo0cbMGHT44IYwJb5xt3p0pJe3x+iYE6mQdKkzxQiA1JhV4RIOfhmi7uy89bzUXE7AkypVTWX9cMJQ/DwAAAAAAAAC7zmyDoTMd/tjHx7rBUFf16Nl04dDYYKiHF8yY4Me966Ub5uTae3j1u2FH6K6X/J0wY4OhC30MNsyaPhgqrT9JMOScWwAAAAAAAIC5MdNHyfygx4Q/4WBI2nv8bLijg6HmThbzmFejHwzlwohUipKpb9qbYMn9umXLwZA/n1ywVUNlfYIhAAAAAAAA2HfmFwy1j4/52+LBj3m0bBeCIRNSdEIX746eccFQvr6s0AY/qlY/ANpiMNQ+3tW8VgTDqYFU1p8kGEq0AwAAAAAAAOw68wuGpLk/V9+xCZLuPHwa3F4bGE0bDJnX2wuG+vU1Oiw6FseH4b+qpfeRuBNmzBx12NLWNiFUv28z7wGBUVl9w7hgKB+gAQAAAAAAAOw6swyG3L9EpvVCIR0c2TZp8BGzGwmGmtBEhx7KQ3F6OuUdQ/n6hiZ4idUJ3XnjMG6OTVhj5xjst+mT2E2EkvqGUcGQPkfhYA0AAAAAAABgLsw0GLo5xwZDu4EJhlKhS/fOmy5jw6sSTMC13eBleDDE3UIAAAAAAACwDAiGKl1CMJQKfTY0d94EgpHtB0PNvrNzHMfQYEgf35bnBgAAAAAAAHAdEAxVOudgSAcd6vGq4lBD3VnUv2vH3M3T1Ap8DlCuPYn9y2KjgqUU9vOLGnv7KWmf6MOyAQAAAAAAAG4YgqFK5xwMAQAAAAAAAAC4EAxVSjAEAAAAAAAAAEuBYKhSgiEAAAAAAAAAWAoEQ5W6wdDz588REREREREREWcrwVClBEOIiIiIiIiIuBQJhiolGEJERERERETEpUgwVCnBEOKyXL2wCm4fa67umP2OnfMU431D/ZSptn3yOs/Dde2La4uIiIi4DAmGKiUYQlyWNYtb1TdkrG9ou2tJH98hY3xLa6h+IUN9Y4bGhwyNnauh47muY/T3Y8+vr9unxNCYIXUQERERcfckGKqUYAg3nouj1YE4uexuvzw5EKuVXHxpj8S507Z91ZzsvqVH54E+pYaPb7uqfabOWa49rbswLjVWJ7Td1e3j1ivVr1WjOzZkSZ+YNWOH7ufyRfk91BzL6oUb+B5q9y390LDvIf/Y/dfbcNv7uIljQkRERMTtO9tg6OzeWqzXjbcfiGe9Pk/Fo9ubPncePvXah0kwNAcvxcmBXNAFAoTpQhuzj4OTy16b3kcikDk/svuXHpyIy0CflKXjdb/BwVDs+KYInuLXR2muUfzaZNtfPBAHL6p5y/18YCWOLsL9lEMXtrFx7vZU7dr91vQv6Vvap1Z/fEkdd4xVB0OJQOb8Q06NDwz4Hiocr/sF52HeW6nQyj+2dn8B3X5DdevU1ywLw/y6bf+Abj9ERERE3G1nGQzpUKgNg5oA6N5jp89jcX/CMMiVYOjm1cFAMlBJBw/a86N0e8bUHFLBkA5r2nHNPCvClZrxY4Kh8PGZ/R2d29cmJAqFY1H1eT8QJyep8587L5njlot5EwbJfolgKLR4LV3Qugtgd0zsa99UW8ia/iV9a/fvWls/1T/WlgqGdFjThjnmGtfc1VMzPhgMXcj37gvyPfyi+rfsZ8iQczDGupr+94kJiUy46vbret3HhIiIiIjbc4bBkAp9bolHF862J3fF2tmmg6NOUDSdo4OhXCAxtn0PzAdDBY45j5cn4iDxiFU8GFJBijfOBiVFj2vVjR8cDGWOz7UbVOVU82/Oee785+aQaN8EQ2qBK/t8rt9HGVq8lixo/T7u69jXviX7cfXrhgz1jemPtdb0dQ2Ns4b6u4bGxIOhwDW1QU3kOnetG98PhtT45n2rx5X9DIkdZ2z7GN2a9hzHdMe5dsOzsLHxqbqIiIiIuJvOLxjSIdBdcdZu2zwydv/J5rX5enpHB0NSvZhOLHrHtsc1d1ocnasFuqrh17Htzhi1gLcLf/X10Xmzf9XP9N/UCNXf1NOBSS8MMH1L7jox4zd1N26OodsnsWhLBBP2+LSB0CMXTEWDod4+7fnzznnMyvH6OAYEQ7njc9X7KA6GHBPn32iOLf6+CLTrhbqcT9Duvuz2dqyz3d/m6/dxX8e+9lVtMWP9Q1+HtsVquJb0sfp9c699U+2xtmgw1Atj5PtAP9IlvwcSjwy2Vo4P3jFkLQyG/GNMnY+xqtqp+qX7zgVD13lMiIiIiLh95xkM2cfILh6IOzoQcsOg5o6iJ6bNfMaQd4fRCKcIhpQ2wIgFAmPbw9ogYROkdBf2pr1TUy3gbbtezJvF+Gb/7gLd1t/UMP3s4smEQNH6heqauTG54CHS7ocpoeBDbUsFWXp+sWDI1tJ3vGzOX9F1rBzvH0upuePbWB7q9cxdH2n0PDaG2+X5+IB8f6u7Pz4nz1Fg4W4Xse6/Md1x/hh/W+pr31hbyfZQn1y7b0kfq+qbMzTOGurvGhqTDIZsYKGvr3zvX6hrrv71+oasHD8mGIodW2z7WG3dVP2yfcvva9kv9CjZdR8TIiIiIl6Psw2Gzh7ecgIfJxhqwiL3A6mf6b7uXUbDnSoY0jaL++jCemx7z0CI4IYNRcGQWQhtwhkzxswhMF6HB14Q1S7m3bHumLTbC4a6c9Xqc+xuy885Fwydq/a2ZuicRawcPywYKr0mpl8u3Imauz7S3HUOt6tFbVPXDQEa3QVsaDGbWuD6bep1aFvoa99YW8n2UJ9cu29JH6vfN/c6ZM3+lLlg6Fy1t49/yfdiZTBUOn5OwZA1VT+/b3MuYsd1U8eEiIiIiNt1po+SdYMf+2HTnTuGOncIue3j3EYwFF0gj23vaRbz1x8MOdv0nJv5ul9XuLVgqD2fvhMGQ6peZ+7e+UlZOX6bwZCu7YdoNeauj7Q2GNKLeLlADVl690NoW0q/v/s6Viu1j5Ix6uuQob4xS/pY3X3EDI2zhvq7hsakHyWT4zqBnwoD5fdAaTBUMX5oMBQ7Lrs91u6q51nQzzc1JlfPfA/ZwKxrbKzdPmSuiIiIiLgbzi8Yah8f87fZO4JCIVAoLBrmZMFQs8iPBgJj24Nmgp9cu96nWQgVB0M6bAkHK6pGLoAImQsMtM5ci9t7cw3pHm+ovZlfKJBpgqf++UkHJK2V47cVDOnjGxMKKXPXRxo9j43BdufxsfgHGBtDC9maxW2ub6w9NW7IGN+SvjX1fEvHqn62rz/GbQsZvXbt41/+tsLvocrx+xQM6XMeCYWUsbF2+5C5IiIiIuJuOL9gSJr7c/X60THnjqJu/0b7yFnlI2ZTBEO5uy3GtscNBDdu8NO0t4vtJogYEwwFwwm9zyNxdBA5BrvfWHCg55E5/lzwEGz3jj/i5tgT7ZEa+nzEzneruQsoNP+y8U7fYFu8vjJ1fLot+95L19fmrk/nfVXRrhbrzd0g2wyGSvoNqR9rL52XcujcQqp+pYbGu9b0TV07Hda0d/zI94F69KnX19wFFApuysY7fSuDodjx+dtLzkNJH9/UmFjb2FAo9hoRERER5+EsgyH3L5FpA3+aXodBtt0PhZQ3FQwNCiwcswvqlGYxHQ+GpG0oo5T7cdudfaeCITO2MRVMRAKNbDAkNeGY1QYVgf1XtUf6+CFJM7/OeXRMBUO9+sF+mz79fZSMN8aDoVR9afT4bODTt9s3Vt+be2sgaNJzCGzPtTvBkFrUhx4hs6pFbImhcf62kH6/knGxPqX7VI7ZT4m1Y1V/f0xom2s61JPvI/05OI3Bfps+/UfESsYb+8GQN7ZVvhebUEW93vSPb0ttV6baUtbXtCFaX3vu1Nf+uNC21HZERERE3F1nGgzdnKODoUVrFv7BsKGjCRjy/XbX7p07XdPBUJlld+akjQdD+fqp4ytx3PzN+6j6bqFKhyxgS8aoPlZ3m9vH1+/vmxuvtDXcvu62Uqcea7eFjPXL3e1VYu4umBKTdwwVWnIOSraVGqtn9duGmKsz1X4QERER8XokGKqUYChlWTA0NnTYDc2xhoKX8cFQU3vkOcreMZSsHz++vOPmr89fYmyuHefv+GBIvgfVnT2dD5mud4pgCBERERFx1yUYqpRgKKUJBGLBkA4q1KNDi1nUqzuf+nfFmLtlmmOtfexPP64nxw0OlrzHvfw6VfXDx5d0kvmnzlmuHZegudtHvo+0lddbf/aPHDc40JHvsXbfY+ogIiIiIs5DgqFKCYYQERERERERcSkSDFVKMISIiIiIiIiIS5FgqFKCIURERERERERcigRDlbrBEAAAAAAAAADAnCEYqpRgCAAAAAAAAACWAsFQpQRDAAAAAAAAALAUCIYqJRgCAAAAAAAAgKVAMFQpwRAAAAAAAAAALAWCoUoJhgAAAAAAAABgKRAMVbpfwdCFOF4ditOr5mXD1emhWK1WjceyV5dc+82ijsnOTXq8W7MDAAAAAAAAuE5mGwyd3VuL9brx9gPxzLZdPBB37HbP+0+6NYa4P8HQlTg9XIlDPxWS6OAnEajk2i+OnWDm8FTuaVpK6+t+BEMAAAAAAACwx8wyGNKhUBsGPRWPbsvX9x73+rXqsOiWeHQRaKt0X4IhHe5EQpUxwZAOY9q6JnyaMpypqU8wBAAAAAAAAPvODIOhx+K+H/I8uSvWieBHB0mp4KjCvQiGrk7FYeARMsvwYCjwaNrFsVgl9lVHXX2CIQAAAAAAANh35hcM6RDorjhrtzV3DMUeFWseLZviMTLlFMGQDiTso07eZ/C0oYoONEwf93GuXLsiVl+P7X3mj/nMnd4+Eo9gxYMfQ7Rdz9ndf3NHj9z/JPlMZX2CIQAAAAAAANh35hkM2cfI2tDHhEOh8OfZw1vdzyAa6dhgSIUmbhahwwknhDHhjbPNu3unpD1e34RAnSxEhSleCKTGhD5byBINfhqi7e6+9LzVXEx4kyhXTmV9giEAAAAAAADYd2YbDJ2pwKd9fCwWDKnHzqa7W0g5Nhjq4QUzJvhx73rphjm59h5e/W4YYkKTbggU2tZlbDB0oY/BhlnTB0Ol9QmGAAAAAAAAYN+Z6aNk7odPK8MB0NR3CylHB0PNnSzmMa9GPxgaErpYMvVNexMsuV+3bDkY8ueTC7ZqqKxPMAQAAAAAAAD7zvyCodBnBult7ucOKU1YdOfhU2fbeMcFQyak6IQu3h0944KhfH03+FG1+gHQFoOh9vGu5rUiGE4NpLI+wRAAAAAAAADsO/MLhqRFf66+9yHVnk3AlOwTcNpgyLzeXjDUr6/RYdGxOD4M/7UuvQ9/jMOYOeowpq1tQqh+32beAwKjsvqGeDA0fP8AAAAAAAAAc2KWwZD7l8i0vT9FX3C30I0EQ01ookMH5aE4PZ3yjqF8fUMTfMTqhO68cRg3xyassXMM9tv0SewmQkl9QzwYGrN/AAAAAAAAgPkw02Do5hwbDO0GJhhKhR7dO2+6jA2vSjABV/iOpqmIB0PXs38AAAAAAACAm4ZgqNIlBEOp0GdD/DGs7QdDzb6zcxxH9o6hLe8fAAAAAAAA4KYhGKp0zsGQDkLU41XFgYe6s6h/14y5m6apFfgcnlx7EvuXxUYFSyns5wc1+vvZ+v4BAAAAAAAAdgeCoUrnHAwBAAAAAAAAALgQDFVKMAQAAAAAAAAAS4FgqFKCIQAAAAAAAABYCgRDlbrB0PPnzxERERERERERZyvBUKUEQ4iIiIiIiIi4FAmGKiUYQkRERERERMSlSDBUKcEQIiIiIiIiIi5FgqFKCYYQERERERERcSkSDFVKMJT38uRArFarxiNxHuhzc56Lo3Zu0qPzAe27dkyIiIiIiIiIw5xtMHR2by3W68bbD8SzTvtjcd+2aW+JRxdu+3AJhvLqYKgXqGw8P3KCmYMTcRnoM8bS+rpfbp6BdhN8EQ4hIiIiIiLi/J1lMKRDoTYMeioe3Zav7z1u2s3rOw+ftv2fPbwVCI+GSTCUNxUM6bClDWsuxclBOpyptab+0GBoG/NGREREREREvAlnGAypu4G8O4Ce3HXuCjJ3C91/4rffFWf29QgJhvLGgyH1GNaBOLl0tp0fiZW/bbB19YcHQ9LLE3Ew2bwRERERERERb8b5BUO9kKe5Y8gJg/QdQl5Q5N5BNEaCobzRYEiHNO4jWM2dN6uVODp3+g21sv6oYKipfXByGWhDREREREREnIfzDIbsY2EXD8QdHQiZcKh/l1A3MJpCgqG8yWDIPual77hRgY0JWCYLhirqjwuG0o/MISIiIiIiIs7B2QZDZ527grrBUOeOoSYg4o6h6zMXDJ2r9vYxrOmDodL6kwRD7ecZISIiIiIiIs7PmT5K5n74tNL9XKHYZwx5n0s0UIKhvOlHyVZemGL+PPxkwVBFfYIhRERERERE3HfnFwy1j4/525rPHdJfeyFQaNtACYbyRoOh9vEuf9tEf/q9sv4kwVCiHREREREREXHXnV8wJE3/uXpzx9DmddPf/6tkTcBU+9fKCIbypgITHba0d9mYx7z6fc1dPt0Pki6zrL7TNxHspNtNbT58GhEREREREefsLIMh9y+RaZ0QyNiEQ62B8IdgaGum76Rpwhod/MSCl02f+kfMSuobRwVD+k4k/lw9IiIiIiIiztuZBkM3J8FQ3ikesdI1thy8DA+GuFsIERERERERlyHBUKUEQ3nHB0PNXT9b/mDnocGQPj4+dBoREREREREXIMFQpQRDec3dPqvGys8Jsn9ZbFSwlNJ+flFjbz8l7RN9WDYiIiIiIiLiDUswVCnBECIiIiIiIiIuRYKhSgmGEBEREREREXEpEgxVSjCEiIiIiIiIiEuRYKhSNxgCAAAAAAAAAJgzBEOVEgwBAAAAAAAAwFIgGKqUYAgAAAAAAAAAlgLBUKUEQwAAAAAAAACwFAiGKiUYAgAAAAAAAIClQDBUKcEQAAAAAAAAACwFgqFKCYZgw4U4Xh2K06vmZcPV6aFYrVaNx7LXdaLmZPctPR6z9/DxbRe1z9Q5y7UDAAAAAABADbMNhs7urcV63Xj7gXjWaX8qHt122u89dtrGSTA0B67E6WE4lJkutDH7OAykJnofiUDm4tjuX3p4KivVUTpe9xscDIWPr3v+htaPXx+F2Uf82uTaAQAAAAAAoJxZBkM6FGrDoCYEasMf8/rOw6eR1+MkGLp5dDCQDFTSwYPm4nhUuJCag26LBCY6rGnHNfOsCFdqxo8JhvLnWGHuTqrahT7vh+L0NHX+c+el/rwBAAAAAABAmBkGQ4/F/fUt8ejC2fbkrljbbRcPxJ31XXHmjtHt3raBjg6GcoHE2PY9oCy0yDDmPF6disPEI1bxYCjwaJYNSooOpm784GAoc3wbTEATumsqjPMYWO785+ZQPEcAAAAAAABIMb9gqBfybB4bu/8k1C7VYZEXJg10dDAk0Qv2xKJ2bHscs5A/vjB3epjHgdw6tr15qVALeBvCqK9lo9m/6tfcudHWCNXf1NOBSS8MMH1LwgUzflN34+YYun0SwUMimLDHpw0EULlgKhoM9fZpz593zmNUjtfHUVS4S+74WsaEM4nzbzDHFn9f5NoBAAAAAACghHkGQ/YxMh34qEDIhEM6GNJ3FPUfJWvvKHJrDXCKYEhhA4zYun1sexgbJGwW8zo8aEMA096pqRbwbjAk96kW45v9uwt0W39Tw/SzAYAJgaL1C9E1c2NywUOk3Q9TuufHoLalAgk9v9CFcY9Vhyqb8xfq3qNy/NBgKHd8uq7ct30vDCJ3fSTR89iQawcAAAAAAIA8sw2Gzh7ecsIeNxiSNoGR+fBp2efJbt0x1NIs7qOL67HtPTLBT67dWcxvwhkzxswhFFKoMMgLotoO7thythcMdeeq0efY3Zafcy4YulDtbc3QOYtQOX5YMFRzTUzfQeFM7vpIcte56H0AAAAAAAAASWb6KNna+0tk5i6hNhjyDT1eNtBtBEPRBfLY9h6BEKEJG8ziOtPuLObrgiFnm55zM1/36wq2Fgy159N3wmBI1evMPXAXVYzK8dsPhiS58xyjYBzBEAAAAAAAwPaZXzDUPj7mb4sHP/qvmE30J+snC4aaRX503T62PUgm+Mm1632axXxxMKTDlnCwomoUBxAORYGAM9cgofbeXEO4xxtGzy90YZrgqX9+CoOVyvHXFgwNCWdy10cSPY8NuXYAAAAAAADIM79gSJr+c/WBvqHQqH3crO5OoimCIfMZLfEAYmx7nEBw01nYm/Z2sd0EEWOCoWA4ofd5LI4PI8dg9xsLDvQ8MsefCx6C7d7xR8gFU6nAQp+P2PluMXcBheZfNt4QPPeaeH1F7vg2mDr9ECldX5O7Ps2xxQOqXDsAAAAAAACUMMtgyP1LZFovFDJhULit9aaCoUGBhUN2QZ3CLKY7WYGq54YAbSjTLOzddmffqWDIjG1MBRORQGMzh/hxmnDMakOiwP6r2hWBPn5I0swvPv14MNSrH+y36dNvLhlviAdDqfqS6PH1z01497H6/fHGQMin55AI/3LtAAAAAAAAUMRMg6Gbc3QwtGjMwj8cFriYYCjfb3fp3rnTJR0MlaFrjAw+4sFQvn7q+EoYN3/zPuJuIQAAAAAAgO1DMFQpwVCKsmBobOiwGzR3vwQOdnww1NQeeY6ydwwl68ePL8+4+evzlxibawcAAAAAAIByCIYqJRhKYQKBWJaggwr16NBiFvXqzqf+XTHmbpnmWGsf+9OP68lxg4Ml+/k+jX6dqvrh40syyfxT5yzXDgAAAAAAADUQDFVKMAQAAAAAAAAAS4FgqFKCIQAAAAAAAABYCgRDlRIMAQAAAAAAAMBSIBiq1A2Gnj9/joiIiIiIiIg4WwmGKiUYQkRERERERMSlSDBUKcEQIiIiIiIiIi5FgqFKCYYQERERERERcSkSDFVKMISIiIiIiIiIS5FgqNL9CobOxdHqQJxcdrdfnhyI1WrVeCTOnbaS9ptVHZOdm/ToPNAHERERERERcT+ccTD0VDy6vRbr9V1xFmg/u6faGm8/EM8CfYa4P8HQpTg5WImDk8temw5+EoFKrv38yAlmDk7EZaDPGEvr634EQ4iIiIiIiLjHzjMYenJXrNe3xKOH6t9+MKRDoTYMagKke487fYa6L8GQDnciocqYYEiHMW1dEz5NGc7U1CcYQkRERERExH13hsHQY3HfhkE6IPKDIdV+Szy6cLbZIMndNtC9CIYuT8RB4BEy6/BgKPBo2vmRWCX2VWddfYIhRERERERE3Hfn/RlDoWCot80+crYW9584/QY6RTCkAwn7qJP3GTxtqKIDDdPHfZwr166M1ddje5/5Yz5zp7ePxCNY8eAn067n7O6/uaNH7v/o3Ok31Mr6BEOIiIiIiIi47y4zGLKPkV08EHd0IGTCoV0IhlRo4oYUOpxwQhgT3jjbvLt3Strj9U0I1AlJVJjihUBqTOizhazR4Kcx2u7uS89bzcWEN5MFQxX1CYYQERERERFx311sMHT28JZss4+P7U4w1NMLZkzw49710g1zcu09vfrdMMSEJt0QKLSt69hg6Fwfgw2zpg+GSusTDCEiIiIiIuK+u9BHyfy/RKY+d2hHgqHmThbzmFejHwwNCV2smfqmvQmW3K9btxwM+fPJBVs1VtYnGEJERERERMR9d3nBUPv4mL/N6zfQccGQCSk6oYt3R8+4YChf3w1+VK1+ALTFYKh9vMvf5odTA62sTzCEiIiIiIiI++7ygiFp0Z+rbwKk0PiU0wZD5vX2gqF+fa0Oi47E0UH4r3XpffhjHMfMUYcxbW0TQvX7NvMeEBiV1Xf6BtuG7x8RERERERFxTs4wGNr8lbGu7p+j9/r4oZDyRoKhJjTRoYPyQJycTHnHUL6+sQk+YnVCd944jptjE9bYOQb7bfrUP2JWUt8YD4bG7B8RERERERFxPs77jqEbcGwwtBuaYCgVenTvvOk6Nrwq0QRc4TuapjIeDF3P/hERERERERFvWoKhSpcQDKVCn43xx7C2Hww1+87OcZzZO4a2vH9ERERERETEm5ZgqNI5B0M6CFGPVxUHHurOov5dM+ZumqZW4HN4cu1J7V8WGxUspbSfH9To72fr+0dERERERETcHQmGKp1zMISIiIiIiIiI6EowVCnBECIiIiIiIiIuRYKhSgmGEBEREREREXEpEgxV6gZDAAAAAAAAAABzhmCoUoIhAAAAAAAAAFgKBEOVEgwBAAAAAAAAwFIgGKqUYAgAAAAAAAAAlgLBUKUEQwAAAAAAAACwFAiGKiUYAgAAAAAAAIClQDBUKcFQnqvTQ7FarRqPxUWzfTe4EMft3KTHuzU7AAAAAAAAgOtkxsHQU/Ho9lqs13fF2aD2YRIM5dHBUCJwuTh2gpnDU3HVbJ+K0vq6H8EQAAAAAAAA7DHzDIae3BXr9S3x6KH6NxD85NpHSDCUJxUM6TCmDWuuxOnhtOFMTX2CIQAAAAAAANh3ZhgMPRb3bdijAyA/+Mm1j5NgKE88GFKPcR2KU/cWnotjsfK3DaauPsEQAAAAAAAA7Dvz/oyhXPBDMHQjRIMhHdK4nznU3NGzWolJ8pnK+gRDAAAAAAAAsO8QDFVKMJQnGQzZx7yuTsWhDmxMeDNZMFRRn2AIAAAAAAAA9h2CoUoJhvLkgqEL1d4+3jV9MFRan2AIAAAAAAAA9h2CoUoJhvKkHyVbOR8OrTB/Pn6yYKiiPsEQAAAAAAAA7DsEQ5USDOWJBkPt413Na4Xe5n4u0Agq6xMMAQAAAAAAwL6zv8HQxQNxZ72uDo4IhvJEgyGJDmPaO3qaD4fu9TV3+XQ/SLqMsvqGeDA0fP8AAAAAAAAAc2KGwdBT8ei2CnR8b4lHFyXtjQRDWyMVDLVhjQ5eYsHMpk+0TJSS+oZ4MDRm/wAAAAAAAADzYd53DN2ABEN50sFQGbpG+wHS2yH1KNl17B8AAAAAAADgpiEYqpRgKM/4YKi5Y6fzIdLTk71jaMv7BwAAAAAAALhpCIYqJRjKY+62MY9iVX9Oj/3LYlt7hst+flCjv5+t7x8AAAAAAABgdyAYqpRgCAAAAAAAAACWAsFQpQRDAAAAAAAAALAUCIYqJRgCAAAAAAAAgKVAMFSpGww9f/4cEREREREREXG2EgxVSjCEiIiIiIiIiEuRYKhSgiFEREREREREXIoEQ5USDCEiIiIiIiLiUiQYqpRgCBERERERERGXIsFQpQRDeS9PDsRqtWo8EueBPjfnuThq5yY9Oh/QvmvHhIiIiIiIiDjMGQdDT8Wj22uxXt8VZ722x+L+WrU13nvstQ+XYCivDoZ6gcrG8yMneDk4EZeBPmMsra/75eYZaDfBF+EQIiIiIiIizt95BkNP7or1+pZ49FD96wdDJjC6/8S+NiHRnYdPnT7DJRjKmwqGdNjShjWX4uQgHc7UWlN/aDC0jXkjIiIiIiIi3oQzDIZU0NOEQTogCt0x1PXs3lqsbz8QzwJttRIM5Y0HQ+oxrANxculsOz8SK3/bYOvqDw+GpJcn4mCyeSMiIiIiIiLejPP+jCGCoZ00GgzpkMZ9BKu582a1EkfnTr+hVtYfFQw1tQ9OLgNtiIiIiIiIiPNwD4IhHiW7bpPBkH3MS99xowIbE7BMFgxV1B8XDKUfmUNEREREREScgwsPhlIfUD1MgqG8uWDoXLW3j2FNHwyV1p8kGGo/zwgRERERERFxfi46GNKPkKkPqb4Itw+RYChv+lGylRemmD8PP1kwVFGfYAgRERERERH33cUGQ88e3po8FFISDOWNBkPt413+ton+9Htl/UmCoUQ7IiIiIiIi4q67yGCoKBS6eCDurOsfMyMYypsKTHTY0t5lYx7z6vc1d/l0P0i6zLL6Tt9EsJNuN7X58GlEREREREScszMMhuznBvnaIMh82HS/fS3uP3HqEAxtzfSdNE1Yo4OfWPCy6VP/iFlJfeOoYEjficSfq0dERERERMR5O+87hm5AgqG8UzxipWtsOXgZHgxxtxAiIiIiIiIuQ4KhSgmG8o4Phpq7frb8wc5DgyF9fHzoNCIiIiIiIi5AgqFKCYbymrt9Vo2VnxNk/7LYqGAppf38osbefkraJ/qwbERERERERMQblmCoUoIhRERERERERFyKBEOVEgwhIiIiIiIi4lIkGKqUYAgRERERERERlyLBUKVuMAQAAAAAAAAAMGcIhiolGAIAAAAAAACApUAwVCnBEAAAAAAAAAAsBYKhSgmGAAAAAAAAAGApEAxVSjAEsCxWL0z+Y1CTqztmv2PnPMV43xiptn3iOs/Dde2LawsAAACwDCb/rS4UpixJgiGAZVGzuFV9Q4aIbXcp6eMzZIxPaQ3VL2QNofEhl0ToeK7rGP392PPrW0tozJA6AAAAALB7TP5bXShMWZIEQ7DhQhyvDsXpVfOy4er0UKxWcvGlPZa9rhM1J7tv6fGYvYePb7uofabOWa49jbswLjVEbLuL28etV6pLqD1ljpI+MWrGDt3P1Uvye6g5ltULN/A91O5b+uFhe/eP3X+9Dba9j5s4JgAAAADYPpP/VhcKU7bjU/Ho9lqs13fFmdf27OEtuV21Nd573GkfI8HQHLgSp4dyQRcIEKYLbcw+DgOpid5HIpC5OLb7lx6eykp1lI7X/QYHQ/HjS53fHN3zH56f6ROvnW1/6VAcvqTmLef5wZU4ftVsDzF0YRsb525P1a7db03/kr6lfWp1sa/9Pr4hdDCUCGQuPuzU+OCA76HC8bqfN49uaNVvt6g2l84Yzylw6wyrab5fUkGcX9fOPyQAAAAAzIfJf3sLhSmT++SuWK9viUcP1b/9YKjrY3F/vRb3n4Ta6iUYunl0MJAMVAqCi4vjdHuG1Bx0WySQ0WFNO66ZZ0V4UzN+TDAUPT593g7F6em482cwdzf1p5g7L5njlot5EwbJfolgKLR4LV3Qugtgd0zsa59UW4ia/iV9a/fvUls/1T/WlgqGdFjThjnmGtfc1VMzPhQMdTF3F6XCR8WQczCG6pqvyu/nF+T39Uvq37Lv6+s+JgAAAADYHpP/9hYKU6ZVBT1NGKQDolwwZO4suvPwaaCt3tHBUC6QGNu+B+SDoQLGnMerU3GYeMQqHgypIMQbZ4OWooOpGz84GIoen9p/c84meR+agCd4V1LmHKfaN8GQWrTHa4QWryULWr+P+zr2tU/Jflz8uiEt7tcx/LHWEKF+vilC/V1DxIOhwDW1oUbsvdKhbnw+GDLBkrlDLU7sOGPbx+DWtOc4pkGdk+Z7WZ+Lsu/rzfguse0AAAAAsLtM/htcKEzZmiXB0MUDcUfdXXQRaBvg6GBIohfsiUXv2PY4ZiF+fKEW+KqGX8e2Ny8VKgCwIYz6Wjaa/at+pv+mRqj+pp4OTHphgukbfmSpixm/qbtxcwzdPokFTiLYsMenDQRQuWAqGgz19mnPn3fOY1SO18dRVLhL7vg0ifNXTDL8MccWf18E2vWiVh5z0O5c7Xaf0DYfv4/7Ova1j2qLGcLdHuqTa/cp6WPx++Ze+6TaY23RYKgXXMj3gX78SX4PZO7a0VSOzwZD6j2cCaX8Y0ydj7Go2qn62X0XBkPXeUwAAAAAsH0m/20uFKZszUQwdHZv8xlDU90tpJwiGFLYACO2bh/bHsYGCZuFjA4P2hDAtHdqqgDADYbkPtVifLN/d4Fu629qmH52oWFCoGj9QnTNscFFpN0PU7rnx6C2pYIsPb/QhXGPVYcim/MX6t6jcvzQYCh3fJrc+U2g5yXnbt9LMaLnsSHcLs/HB5v3t1609+doF7HuvzF97Da3reRrn1hbyfZQn1y7T0kfi+qbM0Wov2uIZDBkHwPT11e+919V11z9q3ukqRwfC4b09mb+sbuFYscW2z4WWzdVP7vvTDB03ccEAAAAANfD5L/NhcKUrVnxKNlUH0A9VTCkaRb30cXx2PYegRDBDRty7U4YsAlnzBgzh8B42dt9/KkbVrhjy9leMNSdq0afY3dbfs65YOhCtbc1Q+csQuX4YcFQ4TXJnd8izL5ic8xd53C7vIZ2YeuGAA3uAja0mE0tcP029Tq0zVJTy1KyPdQn1+5T0sfi9829DlGzP0UuGLpQ7e2dOvJ9VBkMlY4vfZQs1Cd2zLXnopZU/ey+CYYAAAAA9pLJf5sLhSlbsygYkpb2K3AbwVB0gT22vYdZiHfW4U3YYBbPmXYnDKgLhpxtes7NfN2vK9haMNSeT98JgyFVrzP3wF1UMSrH734wJEnUqQ2G3Ls4fEN3dajtPqFtKfz+7utYrdQ+Ssaor0Na3K9jlPSxuPuImSLU3zVE+lEyOa4T+KkwUH4PlAZDFePzwZAkEKbEjstuj7W76HkW9PNJjcnWSwRDsbF2+5C5AgAAAMBuMPlvcqEwZWvWBEO3H4hnobZKJwuGmkV+dN0+tj1IJvjJtet9mkVDcTCkw5ZwsKJqZAOIALnAQOPMNUiovTfXEO7xhtHzC12YJnjqn5/EPF0qx88mGIpcy+h5bAi2q/PRLGzjH2BsCC1kaxa3ub6x9tS4IWN8SvrW1PMpHav62b7+GLctRPTa6esrvwfcEMe55lkqxxcHQ4k701xi5yNE7hzFSI3J1iMYAgAAANhLJv9NLhSmbM2iYMj8ufre5wzpD6VWn0FUdyfRFMGQ+YyVeAAxtj1OILjpLMxNe7vYVgumlXw9IhgKhhN6n8fi+DByDHa/seBBzyNz/M5cgwTbveOPkAumUoGGPh+x891i7gIKzb9svCF47jXx+orc8WmS5zddf4PpFw6h3PdViEi7s0jfZjBU0m9I/Vh76bwUQ+cWQvUrNUdN39S102FNG8TI90HwUS5zF1Ao5Cgbb8gHQ2Y/7h1psePzt5ech5I+Pqkx2XqRYCg2zt8+ZL4AAAAAcPNM/ltcKEyZ1uYzg5oPlt5o//JYv/3+E7+G9KaCoUGBhUOuPYlZTHeyAlXPDQHaUEYp9+O2O/tOBUNmbGMqmIgEGps5xI/ThGNWGxIF9l/Vrgj08UOSZn7x6ceDoV79YL9Nn35zyXhDPBhK1ZdEjy9wbrR+SBer3x8fnb6eQyL8i7U7wZBa1Kf+jLhaxJboE9oWwu9XMi7Wp3SfijH7KaF2rOrvjwltc0mHevJ9pMKcpka436ZP/xGxkvGGfjDkjQ3UV9t8QtsUse2KVFuK+pr9YzJuvr9C40LbFLHtAAAAALC7TP4bXChMWZKjg6FFIxcYcuEfXey3mGAo32936d650yUdDJWha6SCkQLiwVC+fur4Shg3f/M+qr5bqJIhC9iSMaqP1ZIb5/f3yY1X2BpuX3dbqZZQW05LaFuIWL/c3V4l6BqZPyWfI3/HUJ6Sc+CTG5MiVs86Bbk6U+0HAAAAAK6HyX97C4UpS5JgKEVZMDQ2dNgNzLGGgpfxwVBTe+Q5yt4xlKwfP7484+avz19ibK4d5s/4YEi+B9VdMN5n/9QyRTAEAAAAALDrEAxVSjCUwgQCsSxBBxXqEaLFLOrVnU/9OxLM3TLNsdY+9qcf15PjBgdLzWN6Vr9OVf3w8SWZZP6pc5ZrhyVg7vaR7yNt5fXWn5Mjxw0OdOR7rN33mDoAAAAAAPOAYKhSgiEAAAAAAAAAWAoEQ5USDAEAAAAAAADAUiAYqpRgCAAAAAAAAACWAsFQpW4w9Pz5c0RERERERETE2UowVCnBECIiIiIiIiIuRYKhSgmGEBEREREREXEpEgxVSjCEiIiIiIiIiEuRYKhSgiFEREREREREXIoEQ5XuVzB0Lo5WB+Lksrv98uRArFarxiNx7rSVtOM+q95T9r0hPTof0M57ChERERERcSpnHAw9FY9ur8V6fVecBduVts8t8egi1F7v/gRDl+LkYCUOTi57bTr46S3Yy9vPj5yF/8GJuAz0GSP10+5Kfd0v9z4JtJvgkXAIERERERFxCucZDD25a8Keh+rfeDD07OEtsb59S9whGKpWL74ji/oxwZBe7Ld1TfiUqlUr9dPuUn3dN7HvePv080ZERERERNxXZxgMPRb3bRikA6JYMKT6qUDI/hvqU+9eBEOXJ+Ig8AiZdXgwFHg07fxIrBL7qpP6aXer/vBgSJp5jyIiIiIiImKZ8/6MoUQwdHZvLdb3Hsuvdy8Y0gte+6iN90hMG6roBbXp4z7OlWtXxurrsb1HcNRiPrCP9q6PvvHgJ9Ou5+zuv7nzQ+7/6NzpN1Tqp92x+qOCoaZ26FFHRERERERELHeZwdDFA3Gn3b5bwZAKTdxFsl78OiGMCW+cbd6dESXt8fomBOos0tVi3guB1JjUgjsa/DRG29196XmruZgF/mTBBPXj7lj9ccFQ/n2IiIiIiIiIeRcYDJkPnL7z8GnzescfJXMX01IT/Lh3XXTDnFx7T69+d7FtFu3dECi0revYYOhcH4MNs6YPJqgfccfqTxIMyf3Z9zYiIiIiIiLWu7xgSG27/UA8a7ftWDDU3Emh7/qxOovbwaGLNVPftDfBkvt1q1nIby0Y8ueTC7ZqpH7aHatPMISIiIiIiHjzLi4Y0p8ttI7YCYyGOS4YMovkTuiiFtPO4nZcMJSv7wY/qlY/ANpiMNQ+XuRv88OpgVI/7Y7VnyQYSrQjIiIiIiJi3sV++PTGyB1D+nOIVGCUG9912mDIvN5eMNSvr9Vh0ZE4OrCP+3TV+0jciTFmjnqx39Y2IVS/bzPvAYEF9dPuRn2nb6RNmW43tVMBJiIiIiIiIuadYTBkPkOof0dQ7HGxXQqGmtBEL7qVB+LkZMo7hvL1jc3CP1YndOeH47g5NmGBnWOw36ZPbA5xqZ92F+obRwVD+j0aDjYRERERERGx3HnfMXQDjg2GdkMTDKUW/d07P7qODa9KNAHX9hb+1E+77frK4cGQCZ+4WwgREREREXG8BEOVLiEYSoU+G5s7PwILcx0abDUYavadneNQqZ922/WNQ4Mh/f7a8twQERERERH3RYKhSuccDOmFtnq8p3hRre4s6t81Yu4maWoFPocm157U/mWrUcFSQuqn3Xb99vOLGnv7KWmv/+wjREREREREDEswVOmcgyFERERERERERFeCoUoJhhARERERERFxKRIMVUowhIiIiIiIiIhLkWCoUjcYAgAAAAAAAACYMwRDlRIMAQAAAAAAAMBSIBiqlGAIAAAAAAAAAJYCwVClBEMAAAAAAAAAsBQIhiolGAIAAACApbN6YfJlgiZXd8x+x855ivG+MVJt+8R1nofr2hfXFubI5O/aUJiyJAmGAAAAAGDp1CxuVd+QIWLbXUr6+AwZ41NaQ/ULWUNofMglETqe6zpGfz/2/PrWEhozpA7ATTP5uzYUpixJgiHYcCGOV4fi9Kp52XB1eihWK/kfF+2x7HWdqDnZfUuPx+w9fHzbRe0zdc5y7QAAAFCLuzAuNURsu4vbx61XqkuoPWWOkj4xasYO3c/VS/J3zOZYVi/cwO+Y7b6lHx62d//Y/dfbYNv7uIljApiayd+1oTBlOz4Vj26vxXp9V5x5bc8e3pLbVdvGOw+fdvoMlWBoDlyJ00P5H6xAgDBdaGP2cRhITfQ+EoHMxbHdv/TwVFaqo3S87jc4GIod37jgqXv+w+NNn/i1ybVDnOne/xFkQVla6Mvqfu0j31by7aXblfJtvFtseX7yMui6/qm5kvux+wy1Xxd2fkND4djx5djq8TfX1K8pf0wWH+euXZ+b2j+kyV6foT9fZEHVP/vzNYEKFQ5fUm94+d/4D67E8atme4ihC9vYOHd7qnbtfmv6l/Qt7VOri33t9/ENoYOhRCBz8WGnxgcH/I5ZOF738+bRDa367RbV5tIZ4zkFbp36mmVhmF+37R9wMK8ey/H8/gvbY5rvOIdQmDK5T+6K9fqWePRQ/RsJhu497mybSoKhm0cvbpOBSjwYarmQP1xHLIxTc9Btkd/WdFjTjmvmWfGbXc34McFQ+PjM/jYlTUgUCsfKMOP7U8ydl/rztiTy7/8CRr7/o8hJyUvTWbiE3h7yELYWBunFu6w/5vxsc34KVV+dm+j5b87d5NenBHUN5fxOj4efg+zx5djG8TfvTb9mTTDUso35NZS8f0efX9gquesz+OdL8x7O/XxNoRbzJgyS/x1NBEOhxWvpgtZdALtjYl/7pNpC1PQv6Vu7f5fa+qn+sbZUMKTDmjbMMdc4FSL51IwPBUNdTKCSCh8VQ87BGOpq+t8n5phMuBpnW8ekznlu3wBjmPw7LhSmTOtjcd+GQTogmlkwlFuQjW3fA258YSx/cz9MPGIVD4ZUEOKN0/MofVyrbvzgYChzfC7doKoWE/AEg6XcHArnqOY3PLjaTeYQDOlT7n7tMWgxXkjJwjrHNudXhLwwN7XwV+dPL1rVHEaex8Fs4/jlgSwlGIJ5M/jnS/Me1mPdry0FP9c3wZBa4Mb/GxpavJYsaP0+7uvY1z4l+3Hx64a0uF/H8MdaQ4T6+aYI9XcNEQ+GAtdU32FS9vtc7fh8MGRClaEhSmz7GNya9hzHjNENz8LExqfqKpLBj/q9t/haXhPcwbQ4Jv+uC4UpW3OOwZBEL6YTi9qx7XHMQvz4QgUMqoZfx7Y3LxXqFw27CFVfy0azf9XP9N/UCNXf1NML2t4vLaZvyeLdjN/U3bg5hm6fxA+rxC9Q9vi0gQV4bmGu20OBTG+f9vx55zxG5Xh9HEWFu+SOz0Xvo7Bvj2S4Y44t/r7ItTfvwcDcOte3c+7S719Ld3z/esS/v8qIzS/3/jft/ns68v014v0/BXIX0fMiD0Pue6M7R9Wmzocab9ttHb2gdra71l6D1PzkqevUbucnv5CntG1X87THEpuje2wdVC2v3Y71x6i5ysvUQZ+fgeGCPcdqsHw7d86DnoM8Pjs/pbvvkuOLnj+Xpn6wbSjN8fg1/WvdmV/sHAbmV3p9YvX9c+da9f5pjrPt5x1D0fkfgV+///Oz2+42p76/Lbn6Oarm5527Kd7/Cv895zPm+9f8/A78d0cv4GRb0O5/C+x2n9A2H7+P+zr2tY9qixnC3R7qk2v3Kelj8fvmXvuk2mNt0WCot0iXv5OoO35kndxdO5rK8dlgSH5D5IIM/xhT52Msqnaqfum+c8HQsGOSv6up+SXqxq67no8a27i5Vub6Hb/a1O61G7rj+9e/O75/Pc34+t91YTeZ/DswFKZszVQw5H7G0O0H4pnXZ6hTBEMKu8iL/VIztj2MWbi6vzToXyLaxZ9p79SUvyW17epruU+1yNzs34wxC09bf1Oju1g1i9Ro/UJ0zdwYPdfuLzsdIu36fDgT7J4fg9oWDySa+YUujHus6j+YzvkLde9ROd4/llJyx7chEjpk0POS4+x7KUb0PDZE25tzE6qdfu/k3r/mtbvL7vvDjo99f+VJz88Q71Px/TXo/W/q22vnGroMPWQf2TWoHS4PTe6/eSGxC61Ou3y9Ob/ydWjxNmRRVTA/Vbt7/WW73VczXp6udt6qr5qz2tah6euU6hJpl5fDu77O/h1Uv0HnQA6Qb+F2v/7c7XG1tZv+vW+1yPyT588lMn4UzVz1/D077yfn/Vc7v+D1cfqV1C96/0b2b7d35uBQfP4Hkpt7bv+57++ic5MgNz53ffR4Ob92m/yf4vd/sy1kp59k8Pdvg/nvVujnsvxv1Aeb/z7JgzkM/D/9avHn/xvTx25z20q+9om1lWwP9cm1+5T0sai+OVOE+ruGSAZDNljQ11e+B15V11z9q3ukqRwfC4bcoCF290vs2GLbx2LrpuqX7duEJKHjGnxMzblO31ll9utfB/1eiIZJ5tqp/dtxur/zfa9euzX1tWvr2fHO77Sd9g2mbuH7DHaaku+CKkJhytaMBENd1aNn04VDUwVDGvXDQP7HO7o4HtveQ36Ty99iur+4ugvHTLv6ullMbhanZoyZQ2C8+mEmf8Npf6iohWbbwR1bTsni2Z1rkGB7d64afY7dbfk56/n1fyMz+5TzvtC/tNmaoXMWoXK8v8gvo/SamH7Jc5ylqRGZY+46h9r1tuAvxAbT7l3jltC5DLwnXJprYpoD4zvtedLzM6TOS/H31+D3/zSohU+vpnwtp9t7P6m+9pDkoXvnV/5HzFtAySn3ttUSnF8Id//q62b+7hzUnOXl6uL0DRJpl5dNXt/mhSRYewR63k59/1zq19683OvTEpl/D9XPqd9SOr4GuZPY+8te6951b8b03guR+fnnz79eJfX9cx4ksn9/f1lUndy+KrDvj975iuHtP/f9XV3fIzc+d33seHeKQ97/vf1sAznZ/u+HanHZ/Nx3Q4AGdwEbWsymFrh+m3od2mapqWUp2R7qk2v3Kelj8fvmXoeo2Z8iFwxd6EW6/e+2/D2gMhgqHR8LhjaYsaE+sWOuPRe1pOrn990cTyBQVQw5puJAJfD9qjDjY7+jha6d+hmQ+J2us5/A+Mg8NOpnjjyW3KODsNtM/h0YClO2ZlEwJC3tV+A2gqHo4npsew/5TS5/y+n+4iW/yUsXturrZl+bxakZY375CIxXP4TkHNttes7NfN2vK0gtjFucuQYJtbfn09f9Ieoebxg9v95vihK9T1mvM3fv/KSoHL/NYEjX7pyXgSSuU+4699vN3NU5Sh22HqfOY+9clr5/m7G9GoHx6vgSxxAiPj9D8ryUfn8Nev+bc9FvT5/vEMGFkawhS/XmKw+3re9+rVFjnIWjQh5Gb5uL2rfajzU09+jCTW6Tl7gzvt2Xmot8rcq5c1Bzlperi9M3SKy92b/e7n49Eb25evPQx1USPHjjWlLnzyU2fgyR89Ve69DcGkvfq/4+Ou+jwvq5968msv/e94dPaA65fVWi5x+rndl/8fd3YKwl9/0dHR+aW6O9PqPf/w3Rny9TIifr/n7o3sXhW3r3Q2hbCr+/+zpWK7WPkjHq65AW9+sYJX0s7j5ipgj1dw2RDIbUuM7CXf53W24rDoYqxueDIYmu2f1dI3Zcdnus3UXPs6CfT2pMrp75Hgr/3hsba7eH2+XvjDpoyl0f0y/Wx4ZL2s61C43zrqf6OWHH9moExhcEQ7HgDOZB+rtgAKEwZWsWBj7m0bIdC4aaRX70l7ix7UFyC9dMu96n+YbfLE7NmGgwpH85CQcrqkYugAiRXBhbnLkGCbX35hrCPd4wen6hC9P8otY/P4U/RCvHbysY0seXPU+FdN5/XaLnsSF3nvPvLXOsmxq5968JRjp1O/MPjE8cXx5/fob0+39z/VS/6DkY/P6fhuDCSE5Gnt7ee1n1tadAHpJ3fuWY0MIxsGCsIbZwU9vlqd/g7l993czfnYOac2eMwukbJNFu66l99OqOQU5WvnX0fn3tOdfHNWJhnDx/LpHxo2iOLzQnfa2b9qL3f2J+7XtU9XGPrbB+0fs3sv/ge82h+PxPhJqP+37J7b89d5bM/Pz6tXTGy53krs/Y97+lfc9tC/3z3ftvkUIegH18LBouNKgFok9oW4xc31h7atyQMT4lfWvq+ZSOVf1sX3+M2xYieu309ZXX3V3IO9c8S+X44mDICxJixxY7HyFy5yhGakyqLX1nTnys3Z6ca3Peo3faFF9D+fufCpraa2Je96+n8zutv9/O9QqMjwVDOgD0+sIsSbxThxEKU7ZmSTB08UDcWa/FnYdPg9trA6MpgqHc3RZj2+OYRWP3Fy/5zSx/U2t/CMj2diGqfoDIXy7admcxuVmcmjFmAdqvHwwn9D6PxfFh5Bjsfpt99dDzyBy/M9cgwXbv+COkF+ZNe6SGPh+x891iAojQ/MvGG4LnXhOvr0gdn27LvvfS9TcEgpYW930VItfezCFxnRTdc2Rquqes2+7P199Hf7wskJ1DiuA1zL3/9T4T31+KEe//KZCHFZyb2i6n1SKnKY9Fzcwg337e+e22a9S2SP1SUvOTl7NFz9fuv9mvmp78EdZuV3N2x2icvkFS7apNnQdp7Bg78yrEnbOLvgbNNdF9RiyMk+fPJXX8Ej0u0R5E7kS+vYNzsudRXasxx6dRbbKGOm/+t1JR/aZ28v0b2b++Pomxped/0PkN4L53FLn9F31/O/j1a/HH567P2Pe/RR136vqOOf/6vxnypAXrO4u6bQZDJf2G1I+1l85LMXRuIVS/UnPU9E1dOx3WeAv7fl/5u4veV+B3zKLxhnwwZPbjBg+x4/O3l5yHkj4+qTGxtrGhkCU93+aaBEIXdZ5LH8/qXhNz/dywptvuXx9/Dv3xoWBI10w9ngazIvUuHUQoTJnWp+LRbeeDpVtviUcXps/ZvW7b/Sd+DelNBUPyN5HkgnlsexKz8Ov+4iXryd/U2u9n+ZuPCWWUcj9uu7PvVDBkxjYGF5nyh0+0TdLOIX6c5pcfq/2BFNh/Vbsi0Mc9P4pmfvHpy3MTa/TrB/tt+vSbS8YbgqGCJlVfEj2+5roF7PaN1ffm3mt30HNI/Icm196gzoEbHnXfN9LOte3Pzz9/Jhiz7XL/p+73jxnfGeJ/f2VIz29D+P1viX1/BY6vNz7Qp2L+pcjpR6+dapO7NXqLwtKFozztmxrS3PvEJzY/+bbr1lWv7f7VXOQ2NT3dr9mu5ixPoUZ97Y632n3l2i36HCUWqLrdzqsQdc7sPDv4x5XYb27+yfMnKT1+2y/68yOErCHf2vo4XPxr3ZvDgPnZ93Boeqn6ltj7t2T//jl26+fOv2XQ+ZX48/Zrl1z/1Pd3rn6OkvGp6zP2/W+J/XyxDD3/6gCTvx86i7rcYlMtYkv0CW0L4fcrGRfrU7pPxZj9lFA7VvX3x4S2uaRDPfnfcBXmNDXC/TZ9+nd4lIw3dEMGhTc2UF9t8wltU8S2K1JtKeprNmFJQHts6muf0DZFbLul/32p9h//XdeEMo6d0KZ/PfzraUIv2y7389LmZ4QdnwyG9J1CQ9eksIuk36EDCIUpS3J0MLRo5A8Rf2EcxCxcq3/p2SH0wjyyYE4HQ2WU3ZmTRs8xMo9c/dTxlTBu/uZ9NPxuoaGUvn93nfl/f0EatbDc5+trA4bJfwSAhvN7w8jv7UHB0ISohWItJWM2i9BN39w4v79PbrzC1nD7uttKtYTaclpC20LE+uXu9iohdxdMCf1gqJ6Sc+CTG5MiVs86Bbk6NfsZd60DwQ5Ahmm+CxxCYcqSJBhKUbawHhs67AbmWEPBy/hgqKk98hzFg6GS+vHjyzNu/vr8Jcbm2odj5j3q0u0Ay/j+ghj6rofAnQ77hPwRsPfnYJtwfm8Wzj+kGB8Myd911J0k3iNBtUwRDEEKc7fS8GDHXGeCIaiBYKhSgqEU6YW1XrCulrRoVXdm9P8fF3O3THOsqdu6Q+hbweW4wemEuVuk3b9fp6p++PiSTDL/1DnLtY9h3sHQ8r6/wEUHQvK/2Hu9YJTfm/ocJB7ngRFwfm8We/4JhSBB9/Gfyt+H9KM/ctzgQEf+Dtbue0wd2D4EQ1APwVClBEMAAAAAAAAAsBQIhiolGAIAAAAAAACApUAwVCnBEAAAAAAAAAAsBYKhSt1g6Pnz54iIiIiIiIiIs5VgqFKCIURERERERERcigRDlRIMISIiIiIiIuJSJBiqlGAIEREREREREZciwVClBEOIiIiIiIiIuBQJhirdr2DoXBytDsTJZXf75cmBWK1WjUfi3Gkracd9Vr2n7HtDenQe6IOIiIiIiIjX5YyDoafi0e21WK/virNku/HOw6eBPvXuTzB0KU4OVuLg5LLXpoOfxII+135+5AQDByfiMtBnjNRPuyv1dT+CIURERERExBt1nsHQk7tivb4lHj1U/4aCocfi/oRhkOu+BEM63Iks6scEQzoMaOua8GnKcID6aXepvu474b4RERERERGx3hkGQyr0acIgHRD1g6Gze2uxvve4s20q9yIYujwRB4FHyKzDg6HAo2nnR2KV2Fed1E+7W/UJhhAREREREW/eeX/GUDAYMo+Q3X/ibpvOKYIhvSC2j9p4n8HThip6QW36uI9z5dqVsfp6bO8zf9RiPrCP9q6PvvHgJ9Ou5+zuv7mjRO7/6NzpN1Tqp92x+gRDiIiIiIiIN+8CgyF1R9Et8ejJA3Gn+Xwh/djZhdtnuGODIRWauItkvTh2QhgT3jjbvLt3Strj9U0I1Fmkq8W8FwKpMaHPFrJGg5/GaLu7Lz1vNRcTHkwWTFA/7o7VJxhCRERERES8eZcXDF00gdDtB+JZs+3Zw1uBAGmYY4Ohnu5iWmqCH/eui26Yk2vv6dXvLsbNor0bAoW2dR0bDJ3rY7Bh1vTBBPUj7lh9giFERERERMSbd7l3DHXuEDIfRj3F42Wjg6HmTgp9149VLqY7wdCQ0MWaqW/am2DJ/brVLOS3Fgz588kFWzVSP+2O1ScYQkREREREvHkXGgz5IVAoLBrmuGDILJI7oYtaTDsL6XHBUL6+G/yoWv0AaIvBUPt4kb/ND6cGSv20O1afYAgREREREfHmXWAw1Dw65jxKpv9KmfNaax85q3zEbNpgyLzeXjDUr6/VYdGRODqwj/t01fvwxziOmaMOA9raJoTq923mPSCwoH7a3ajv9A22Dd8/IiIiIiIi1jnDYMj81THzodKu3TuCdBhk2/xQSHkjwVATmuhFr/JAnJxMecdQvr6xWXjH6oTu/HAcN8cmLLBzDPbb9InNIS710+5CfWM8GBqzf0RERERERKxx3ncM3YBjg6Hd0ARDqUV3986PrmPDqxJNwBW+o2kKqZ922/WV8WDoevaPiIiIiIiIBEPVLiEYSoU+G5u7NgILd71o32ow1Ow7O8ehUj/ttusbs3cMbXn/iIiIiIiISDBU7ZyDIb0QV4/3FC+41Z1F/bs2zN0cTa3A58Dk2pPav2w1KlhKSP20267ffn5Qo7+fre8fERERERERXQmGKp1zMISIiIiIiIiI6EowVCnBECIiIiIiIiIuRYKhSgmGEBEREREREXEpEgxV6gZDAAAAAAAAAABzhmCoUoIhAAAAAAAAAFgKBEOVEgwBAAAAAAAAwFIgGKqUYAgAAAAAAAAAlgLBUKUEQwAAAAAAAACwFAiGKiUYAgAAAAAAAIClQDBUKcFQnqvTQ7FarRqPxUWzHUDId8Nx+96QHvvvjpJ23lMAAAAAAABTMeNg6Kl4dHst1uu74szdfvFA3Fmr7X3vP3H6DZRgKI8OhnoL+g0Xx87C//BUXDXbp4L6aXalvu6Xe58E2k3wSDgEAAAAAAAwBfMMhp7cFev1LfHoofrXC4ZC6rBI9r8ItFVKMJQnFQzpxX4bFlyJ08N0OFAL9dPsUn3dN7HvePv08wYAAAAAANhXZhgMPRb3bRikA6J8MHR2by3W9x4H22olGMoTD4bUY0CH4tSkBoaLY7Hytw2G+ml2q/7wYEhydSoOJ5s3AAAAAADA/jLvzxgqCYaaR8umeIxMSTCUJxoM6ZDAfQSoufNjtRKT3PxB/TQ7Vn9UMNTUPiQZAgAAAAAAGMXig6FnD2+J9e0H4lmgbYgEQ3mSwZB9zEjf8aECA7PAnyyYoH6cHas/LhhSu4g/sggAAAAAAABlLDwYUo+dTXe3kJJgKE8uGLpQ7e1jQNMHE9SPsGP1JwmG5P70bgAAAAAAAGAQiw6Gpr5bSEkwlCf9KJlc7HcW8+pzaSYMJqgfZ8fqEwwBAAAAAADcPAsOhszdQncePg20DZdgKE80GGofL2peK/Q293NpRkD9NDtWf5JgKNEOAAAAAAAAeZYbDOUeM2s+lDr9KFpfgqE8qQW7Xuy3d3mYx4z6fc1dJt0PMi6D+ml2o75B9420KdLtpjYfPg0AAAAAADCOGQZDT8Wj2yrQ8b0lHl3YPgV3CxEMbY30nRxNWKCDh9jCf9MnkRtEoH6aXahvGBUM6TuR7OcYAQAAAAAAwFDmfcfQDUgwlGeKR3x0jS0u/KmfZtv1FcODIRM+cbcQAAAAAADAeAiGKiUYyqNDhVHBUHPXSftI0tRQP8226xuGBkP6/bXluQEAAAAAAOwLBEOVEgzlMXebyEW9tvJzauxfthoVLCWgfppt128/v6ixt5+S9vrPPgIAAAAAAIAwBEOVEgwBAAAAAAAAwFIgGKqUYAgAAAAAAAAAlgLBUKUEQwAAAAAAAACwFAiGEBERERERERH31MmDIQAAAAAAAAAAmAcEQwAAAAAAAAAAewrBEAAAAAAAAADAnkIwBAAAAAAAAACwpxAMAQAAAAAAAADsKQRDAAAAAAAAAAB7CsEQAAAAAAAAAMCeQjAEAAAAAAAAALCnEAwBAAAAAAAAAOwpBEMAAAAAAAAAAHuJEP8/q9XQP3imrIIAAAAASUVORK5CYIIA" alt="" width="803" height="312" />

那  tile(inX, (dataSetSize,1))的意思就是，让inX矩阵，在列重复1次。在行方向上重复dataSetSize次了。diffMat得到了目标与训练数值之间的差值。

　而 sum(axis=1) 为什么这样写呢，因为python和c不一样。 小编开始也不懂然后 在命令行输入help(sum) 出来很多有用的帮助。自己亲手敲了几行就懂了。

 axis=None, will sum all of the elements of the input array.  If
        axis is negative it counts from the last to the first axis.

 

b = ([[ 0,  5,  6,  4, 66,  0,  5,  6,  4, 66],

       [ 0,  5,  6,  4, 66,  0,  5,  6,  4, 66]])

a = [0, 5, 6, 4, 66]

 

sum(b,axis=0)

Out[87]: array([  0,  10,  12,   8, 132,   0,  10,  12,   8, 132])

sum(b,axis=1)

Out[88]: array([162, 162])

　写到这想必大家也懂了。如果想搞机器学习，还需要了解很多python数学函数啊。

下面是get() 它是dictionary（字典）的一个函数。

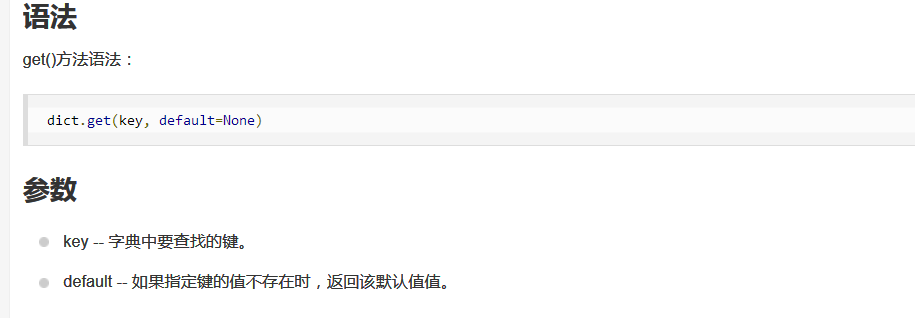
所以classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 的意思就是查找classcount字典中和voteIlabel相同的元素，默认返回0，因为是从0开始的，所以要加1

sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) key指定一个元素的迭代方法进行排序classCount。并且是倒序。

下面是变量表:最后输出结果是0

 

 '''
 Created on Sep 16, 2010
 kNN: k Nearest Neighbors

 Input:      inX: vector to compare to existing dataset (1xN)
             dataSet: size m data set of known vectors (NxM)
             labels: data set labels (1xM vector)
             k: number of neighbors to use for comparison (should be an odd number)

 Output:     the most popular class label
  @author: pbharrin
 '''
 from numpy import *
 import operator   #运算符模块
 from os import listdir

 #inX：用于分类的输入向量。即将对其进行分类。
 #dataSet：训练样本集
 #labels:标签向量
 def classify0(inX, dataSet, labels, k):
     dataSetSize = dataSet.shape[0]#得到数组的行数，即有几个训练数据
     diffMat = tile(inX, (dataSetSize,1)) - dataSet #tile:numpy中的函数。tile将原来的一个数组，扩充成了4个一样的数组。diffMat得到了目标与训练数值之间的差值。
     sqDiffMat = diffMat**2#差值的平方
     sqDistances = sqDiffMat.sum(axis=1)#对应列相乘，即距离和
     distances = sqDistances**0.5 #开根号
     sortedDistIndicies = distances.argsort()#升序排列
     classCount={}         #选择距离最小的k个点
     for i in range(k):
         voteIlabel = labels[sortedDistIndicies[i]]
         classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
     sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
     return sortedClassCount[0][0]

 def createDataSet():
     group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
     labels = ['A','A','B','B']
     return group, labels

 def file2matrix(filename):
     fr = open(filename)
     numberOfLines = len(fr.readlines())         #get the number of lines in the file
     returnMat = zeros((numberOfLines,3))        #prepare matrix to return
     classLabelVector = []                       #prepare labels return
     fr = open(filename)
     index = 0
     for line in fr.readlines():
         line = line.strip()                     #Python strip() 方法用于移除字符串头尾指定的字符（默认为空格）。
         listFromLine = line.split('\t')          #将line按'\t'进行分割
         returnMat[index,:] = listFromLine[0:3]
         classLabelVector.append(int(listFromLine[-1]))  #倒数第一个元素
         index += 1
     return returnMat,classLabelVector
  #归一化特征值
  #使得所有参量在0到1之间
 def autoNorm(dataSet):
     minVals = dataSet.min(0)
     maxVals = dataSet.max(0)
     ranges = maxVals - minVals
     normDataSet = zeros(shape(dataSet))
     m = dataSet.shape[0]  #返回矩阵第二维长度(列数)
     normDataSet = dataSet - tile(minVals, (m,1))
     normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide
     return normDataSet, ranges, minVals

 def datingClassTest():
     hoRatio = 0.50 #hold out 10%
     datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #load data setfrom file
     normMat, ranges, minVals = autoNorm(datingDataMat)
     m = normMat.shape[0]       #m:目录中有多少文件#shape函数是numpy.core.fromnumeric中的函数，它的功能是查看矩阵或者数组的维数。
     numTestVecs = int(m*hoRatio)
     errorCount = 0.0
     for i in range(numTestVecs):
         classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
 #inX：用于分类的输入向量。即将对其进行分类。normMat[i,:],
 #dataSet：训练样本集.normMat[numTestVecs:m,:]
 #labels:标签向量.datingLabels[numTestVecs:m]
 #k:3
         print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
         if (classifierResult != datingLabels[i]): errorCount += 1.0
     print ( "the total error rate is: %f" % (errorCount/float(numTestVecs)))
     print (errorCount)
 '''
 我们将一个32x32二进制图像矩阵转换为1x1024的向量
 '''
 def img2vector(filename):   #图片转化为向量
     returnVect = zeros((1,1024))
     fr = open(filename)
     for i in range(32):
         lineStr = fr.readline()
         for j in range(32):
             returnVect[0,32*i+j] = int(lineStr[j])
     return returnVect
 #安照先训练再测试的模式
 def handwritingClassTest():
     hwLabels = []
     trainingFileList = listdir('trainingDigits')           #load the training set listdir法用于返回指定的文件夹包含的文件或文件夹的名字的列表
     m = len(trainingFileList)  #获取文件长度
     trainingMat = zeros((m,1024))
     for i in range(m):
         fileNameStr = trainingFileList[i]      #从文件名解析分类数字
         fileStr = fileNameStr.split('.')[0]     #take off .txt
         classNumStr = int(fileStr.split('_')[0])
         hwLabels.append(classNumStr)
         trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)  #将文件名
     testFileList = listdir('testDigits')        #iterate through the test set
     errorCount = 0.0
     mTest = len(testFileList)
     for i in range(mTest):
         fileNameStr = testFileList[i]
         fileStr = fileNameStr.split('.')[0]     #take off .txt
         classNumStr = int(fileStr.split('_')[0])
         vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
         classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 4)
         print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr))
         if (classifierResult != classNumStr): errorCount += 1.0
     print ("\nthe total number of errors is: %d" % errorCount)
     print ("\nthe total error rate is: %f" % (errorCount/float(mTest)))
 # main part
 handwritingClassTest();

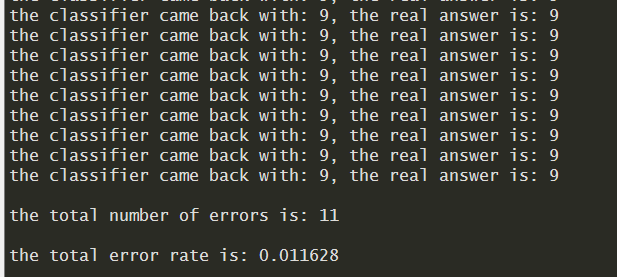
k临近算法手写识别，错误率为1.2%，改变k的值，修改函数handwriting - classTest 随机选取的训练样本，改变训练样本的个数，都会对k临近算法错误率产生影响。

　　代码下载地址    http://www.ituring.com.cn/book/download/0019ab9d-0fda-4c17-941b-afe639fcccac