吴恩达深度学习笔记（deeplearning.ai）之卷积神经网络（一）

Padding

在卷积操作中，过滤器（又称核）的大小通常为奇数，如3x3，5x5。这样的好处有两点：

• 在特征图（二维卷积）中就会存在一个中心像素点。有一个中心像素点会十分方便，便于指出过滤器的位置。

• 在没有padding的情况下，经过卷积操作，输出的数据维度会减少。以二维卷积为例，输入大小 \(n\times n\)，过滤器大小\(f\times f\)，卷积后输出的大小为\((n-f+1)\times(n-f+1)\)。
• 为了避免这种情况发生，可以采取padding操作，padding的长度为\(p​\)，由于在二维情况下，上下左右都“添加”长度为\(p​\)的数据。构造新的输入大小为\((n+2p)\times(n+2p)​\) , 卷积后的输出变为\((n+2p-f+1)\times(n+2p-f+1)​\)。

• 如果想使卷积操作不缩减数据的维度，那么\(p\)的大小应为\((f-1)/2\)，其中\(f\)是过滤器的大小，该值如果为奇数，会在原始数据上对称padding，否则，就会出现向上padding 1个，向下padding 2个，向左padding 1个，向右padding 2个的情况，破坏原始数据结构。

Stride

卷积中的步长大小为\(s\)，指过滤器在输入数据上，水平/竖直方向上每次移动的步长，在Padding 公式的基础上，最终卷积输出的维度大小为：

\[\left \lfloor \frac{n+2p-f}{s}+1 \right \rfloor \times \left \lfloor \frac{n+2p-f}{s}+1 \right \rfloor\]

\(\left \lfloor \right\rfloor\)符号指向下取整，在python 中为floor地板除操作。

Channel

通道，通常指数据的最后一个维度（三维），在计算机视觉中，RGB代表着3个通道(channel)。

• 举例说明：现在有一张图片的大小为\(6\times 6\times 3\)，过滤器的大小为\(3\times 3\times n_c\), 这里\(n_c\)指过滤器的channel大小，该数值必须与输入的channel大小相同，即\(n_c=3\)。
• 如果有\(k\)个\(3\times 3\times n_c\)的过滤器，那么卷积后的输出维度为\(4\times 4\times k\)。注意此时\(p=0, s=1\)，\(k\)表示输出数据的channel大小。一般情况下，\(k\)代表\(k\)个过滤器提取的k个特征，如\(k=128\)，代表128个\(3\times 3\)大小的过滤器，提取了128个特征，且卷积后的输出维度为\(4\times 4\times 128\)。

在多层卷积网络中，以计算机视觉为例，通常情况下，图像的长和宽会逐渐缩小，channel数量会逐渐增加。

Pooling

• 除了卷积层，卷积网络使用池化层来缩减数据的大小，提高计算的速度 ，同时提高所提取特征的鲁棒性。 池化操作不需要对参数进行学习，只是神经网络中的静态属性。
• 池化层中，数据的维度变化与卷积操作类似。池化后的channel数量与输入的channel数量相同，因为在每个channel上单独执行最大池化操作。
• f=2, s=2，相当于对数据维度的减半操作，f指池化层过滤器大小，s指池化步长。

卷积神经网络示例

一个用于手写数字识别的CNN结构如下图所示：

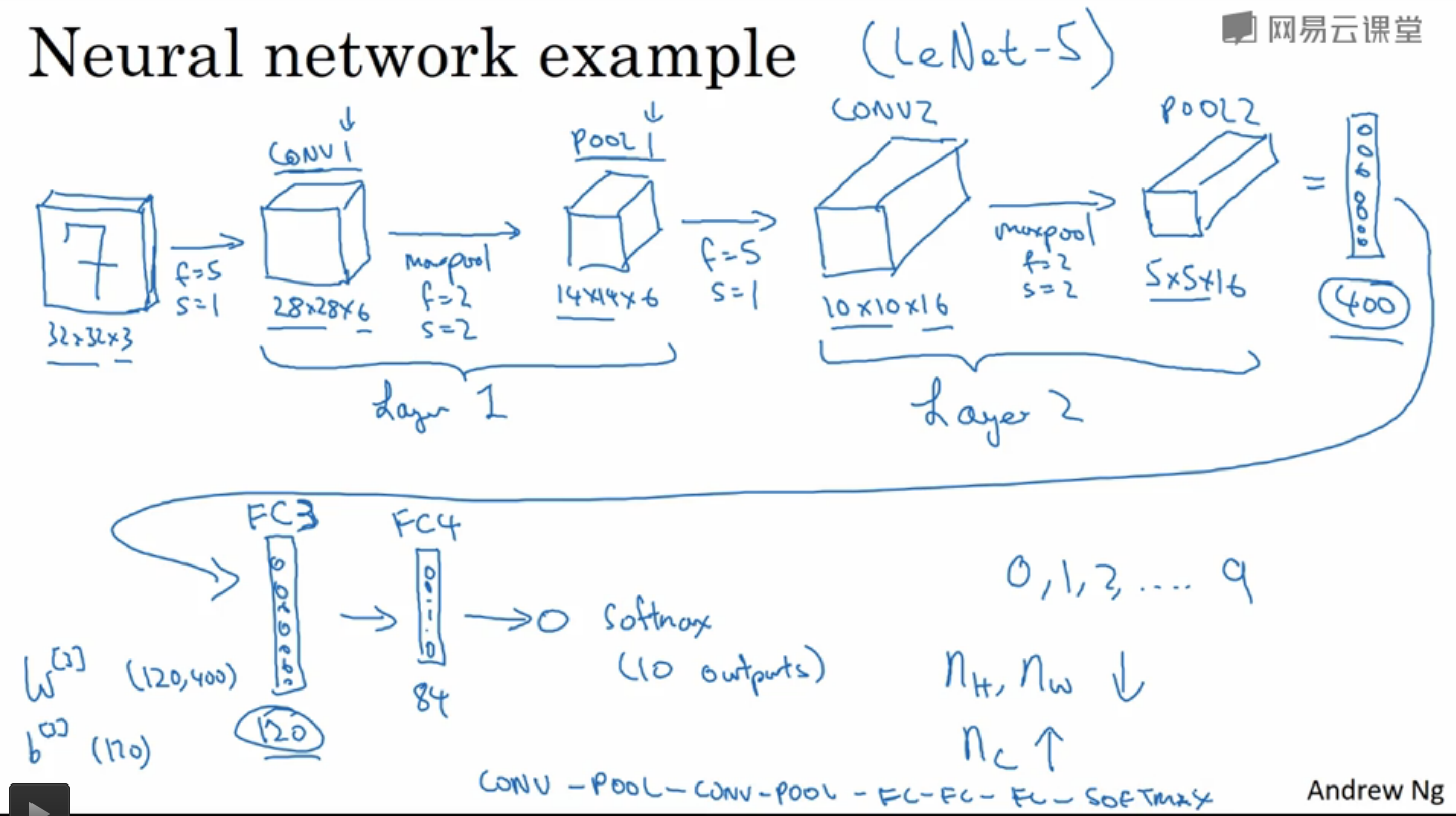
该网络应用了两层卷积，并且在第二个池化层之后又接了几个全连接层，这样做的目的是避免某一层的激活值数量减少的太快，具体原因后文解释。

具体参数数量可视化如下所示：

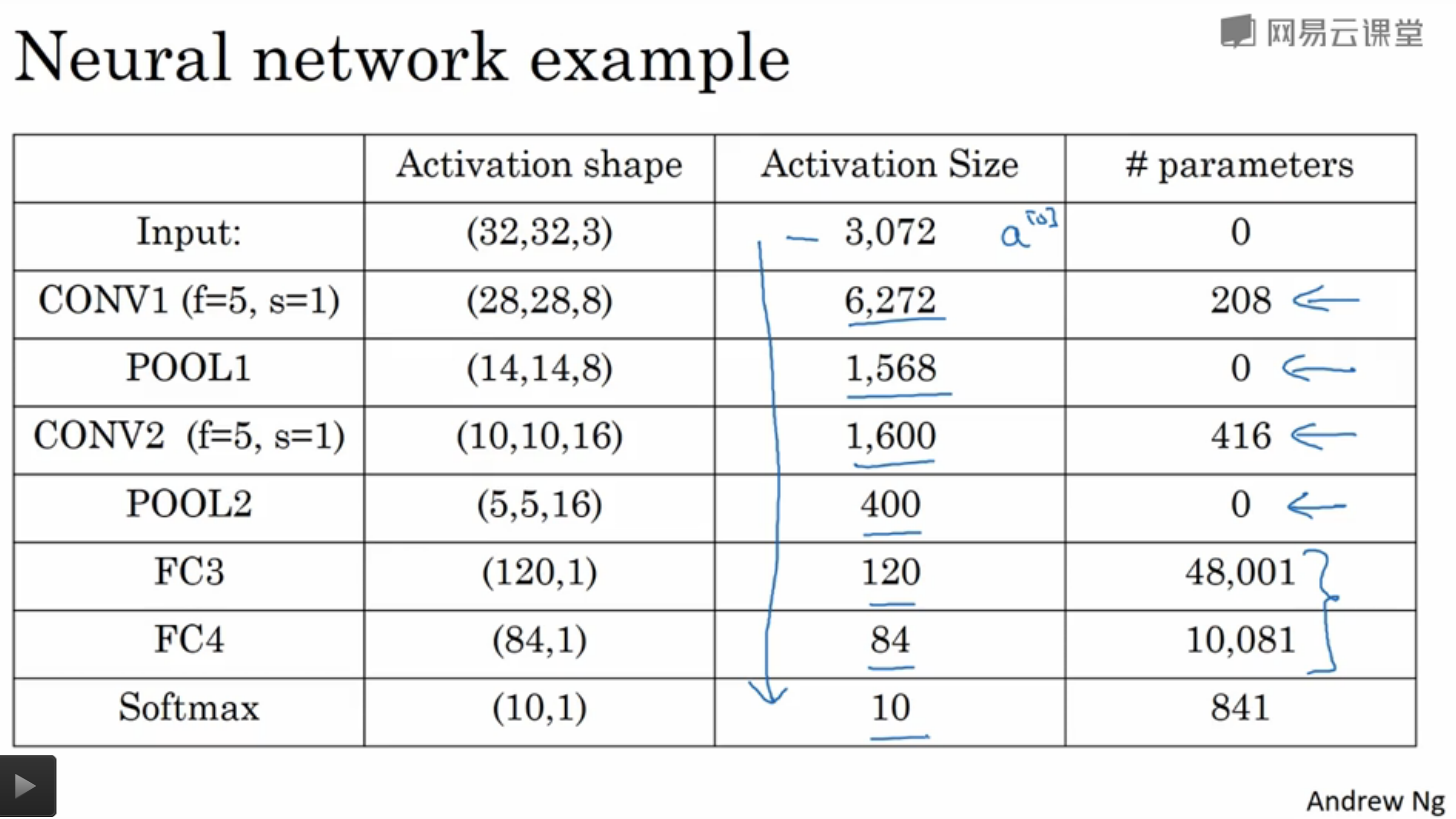
从图中可以发现，卷积层的参数数量较小，大部分参数集中在全连接层。而且随着网络层的加深，激活值数量逐渐减少，如果激活值数量下降太快，会影响网络的性能。因此需要构建多个全连接层，而不是一个全连接层一步到位。

卷积层的好处

与只用全连接层相比，卷积层的主要优点是参数共享和稀疏连接，这使得卷积操作所需要学习的参数数量大大减少。