Fresnel integral菲涅尔积分的一丢丢探讨

起因源于导师的关于回旋曲线的一点问题

其中最后得到的曲率公式中的c，s’和s定义不明确

于是开始从头从（2.1）式中的积分入手探究

维基百科中Fresnel integral的S(x)与C(x)的定义为：

可以看出（2.1）式与之不同，多了常数1/c，这里是我认为的常数...

而在维基百科中，有着如下结论

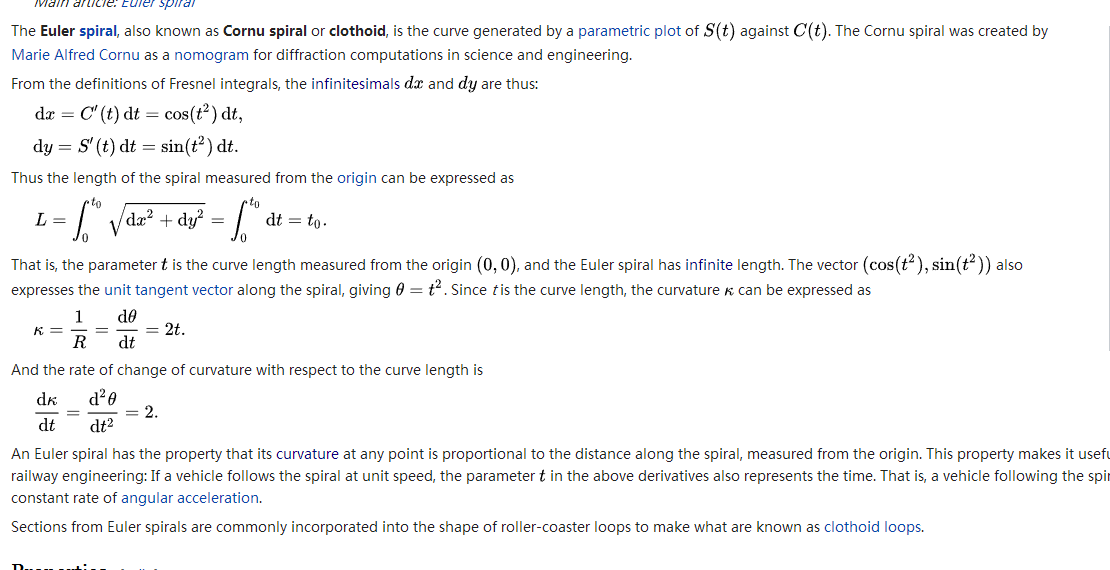
大致的意思就是回旋曲率与回旋段的距离呈线性关系

其中t即为从原点测量的曲线长度，又因为cos（t²）和sin（t²）表示沿螺旋的单位切线向量，则可令θ=t²

由于曲率是单位切向量对于弧长的旋转速度，故可得到k=2t

发现k=2c²s和k=2t如此相似

我对（2.1）式代入（2.2）式，可得到k=2cs'

由于提到s‘=cs，因此k=2c²s

那么，c是控制曲率沿着段变化的速率，s表示回旋段的距离

This parameter c controls the rate that the curvature changes along the segment

s’ = cs and s is the distance measured along the clothoid segment