Bellman-Ford&&SPFA算法详解

Dijkstra在正权图上运行速度很快，但是它不能解决有负权的最短路，如下图：

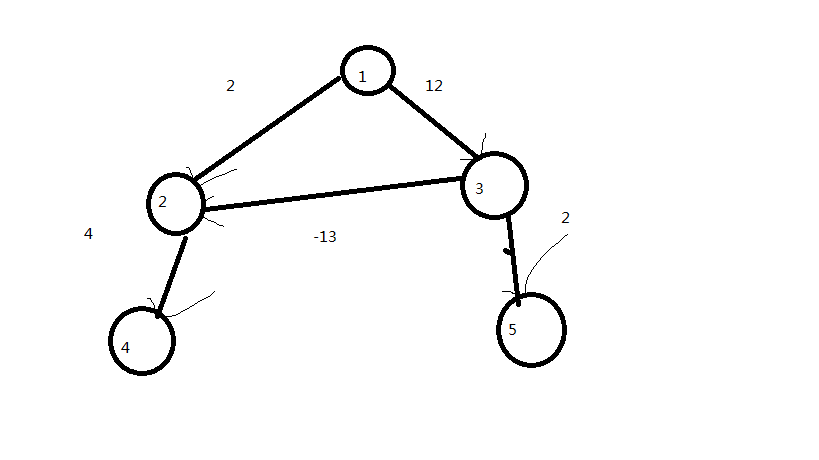
Dijkstra运行的结果是（以1为原点）：0 2 12 6 14；

但手算的结果，dist[4]的结果显然是5，为什么会出现这种情况呢？原因很显然，Dijkstra认为，从一个更长的边过来不会比一个更短的边过来更短（读起来很绕口，但请读者好好理解这句话！）但是由于出现了负权边，可以“救回来”，就像松弛2号节点一样。

Bellman_Ford:

知道了Dijkstra为什么不能做负权图之后，我们来看看Bellman-ford算法。它的基本思想是：图的最短路，既不会包含正环（可以不走），更不能有负环（否则一直走就可以无限小），因此最多经过n-1条边（每个节点都经过一次），bellman-ford实际上是枚举距离源点多少条边，尝试对每条边松弛的过程。请读者联系上图，自行推导一下Bellman_ford的运行过程

样例如下：

5 5
1 2 2
1 3 12
3 2 -13
2 4 4
3 5 2

朴素Bellman_Ford算法的时间复杂度是O(NM)；程序如下：

 #include<iostream>
 #include<cstdio>
 #include<queue>
 #include<cstring>
 using namespace std;
 int n,m,s,dist[],v[],w[],u[],cnt,x,y,z;
 void bellman_ford(int s)
 {
     memset(dist,,sizeof(dist));
     dist[s]=;
     for(int i=;i<=n-;i++)
     {
         for(int j=;j<=m;j++)
         {
             dist[v[j]]=min(dist[v[j]],dist[u[j]]+w[j]);
         }
     }
 }
 int main()
 {
     scanf("%d %d",&n,&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d %d %d",&u[i],&v[i],&w[i]);
     }
     bellman_ford();
     for(int i=;i<=n;i++)
     {
         cout<<dist[i]<<" ";
     }
     return ;
 }

SPFA:

SPFA是对Bellman_Ford算法的优化，它采用队列保存即将松弛其他点的节点，每次选与队首相连的点进行松弛，可以使用链式前向星（邻接表）实现，避免了Bellman_Ford算法许多无效的松弛操作，平均复杂度O(KM)，K为平均松弛次数，也有可能被网格图卡回O(NM)，是不稳定的算法。程序如下：

 #include<iostream>
 #include<cstdio>
 #include<queue>
 #include<cstring>
 using namespace std;
 int n,m,s,dist[],v[],w[],nxt[],head[],cnt,x,y,z;
 bool vis[];
 void add(int a,int b,int c)
 {
     v[++cnt]=b;
     w[cnt]=c;
     nxt[cnt]=head[a];
     head[a]=cnt;
 }
 void SPFA(int s)
 {
     memset(dist,,sizeof(dist));
        queue<int>q;
     dist[s]=;
     vis[s]=;
     q.push(s);
     while(!q.empty())
     {
         int c=q.front();
         q.pop();
         vis[c]=;
         for(int i=head[c];i;i=nxt[i])
         {
             int y=v[i];
             if(dist[y]>=dist[c]+w[i])
             {
                 dist[y]=dist[c]+w[i];
                 if(!vis[y])
                 {
                     q.push(y);
                     vis[y]=;
                 }
             }
         }
     }
 }
 int main()
 {
     scanf("%d %d",&n,&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d%d%d",&x,&y,&z);
         add(x,y,z);
     }
     SPFA();
     for(int i=;i<=n;i++)
     {
         cout<<dist[i]<<" ";
     }
     return ;
 }