什么是NFA(不确定的有穷自动机)和DFA(确定的有穷自动机)

本节知识点是《编译原理》第三章-词法分析，学习参考教材为清华大学出版社《编译原理》第三版：

前情提要：

字母表∑1和∑2的乘积( product)：

　　∑1∑2 ={ab|a ∈∑1, b ∈ ∑2}

　　例： {0, 1} {a, b} ={0a, 0b, 1a, 1b}

字母表∑的n次幂( power)：长度为n的符号串构成的集合

　　∑0 ={ ε }
　　∑n =∑n-1 ∑ , n ≥

　　例： {0, 1}3 ={0, 1} {0, 1} {0, 1}={000, 001, 010, 011, 100, 101, 110, 111}

字母表的正闭包（positive closure）：长度正数的符号串构成的集合：

　　∑+ = ∑ ∪∑2 ∪∑3 ∪…

　　例：{a, b, c, d }+ = {a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}

字母表的克林闭包（Kleene closure）：任意符号串（长度可以为零）构成的集合：

　　∑* = ∑0 ∪∑+ = ∑0 ∪∑ ∪∑2 ∪∑3 ∪…

　　例：{a, b, c, d }* = {ε, a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}

一、【 有穷自动机 】：

1、定义

 有穷自动机 ( Finite Automata，FA )由两位神经物理学家MeCuloch和Pitts于1948年首先提出，是对一类处理系统建立的数学模型
 这类系统具有一系列离散的输入输出信息和有穷数目的内部状态（状态：概括了对过去输入信息处理的状况）
 系统只需要根据当前所处的状态和当前面临的输入信息就可以决定系统的后继行为。每当系统处理了当前的输入后，系统的内部状态也将发生改变

2、Finite Automata的典型例子：

 电梯控制装置
 输入：顾客的乘梯需求（所要到达的层号）
 状态：电梯所处的层数+运动方向
 电梯控制装置并不需要记住先前全部的服务要求，只需要知道电梯当前所处的状态以及还没有满足的所有服务请求

3、Finite Automata模型示意：

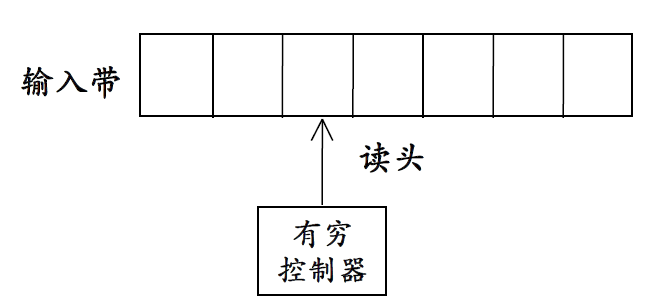
 输入带(input tape)：用来存放输入符号串
 读头(head )：从左向右逐个读取输入符号，不能修改（只读）、不能往返移动
 有穷控制器( finite control )：具有有穷个状态数，根据当前的状态和当前输入符号控制转入下一状态

4、FiniteAutomata的表示：

 转换图 (Transition Graph)
　　 结点：FA的状态
　　 初始状态（开始状态）：只有一个，由start箭头指向
　　 终止状态（接收状态）：可以有多个，用双圈表示
　　 带标记的有向边：如果对于输入a，存在一个从状态p到状态q的转换，就在p、q之间画一条有向边，并标记上a

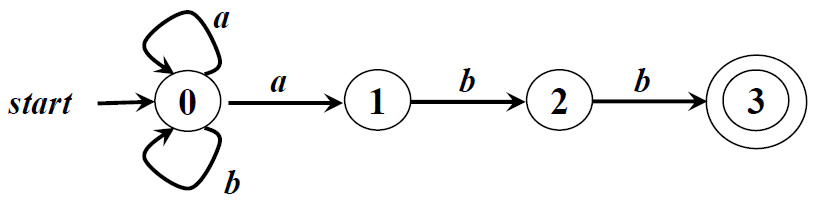
5、Finite Automata定义(接收)的语言

 给定输入串x，如果存在一个对应于串x的从初始状态到某个终止状态的转换序列，则称串x被该FA接收
 由一个有穷自动机M接收的所有串构成的集合称为是该FA定义（或接收）的语言，记为L(M （machine）)

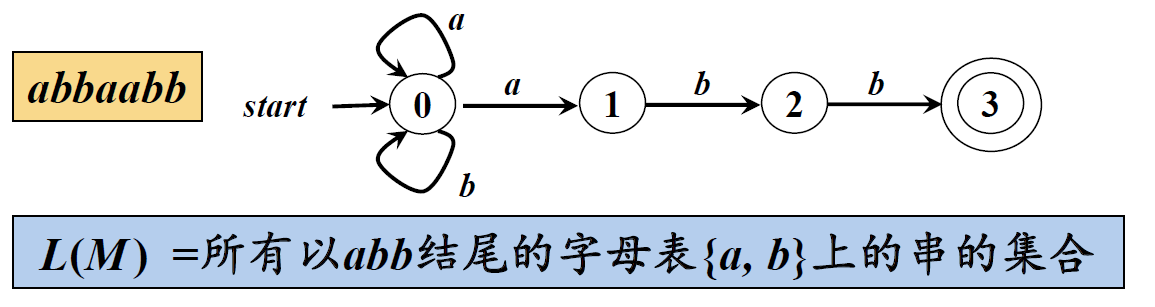
6、最长子串匹配原则(Longest String Matching Principle )

·当输入串的多个前缀与一个或多个模式匹配时，总是选择最长的前缀进行匹配

·在到达某个终态之后，只要输入带上还有符号， DFA就继续前进，以便寻找尽可能长的匹配

二、【 有穷自动机的分类 】：

　

　　 确定的FA (Deterministic finite automata, DFA)
　　 非确定的FA (Nondeterministic finite automata, NFA)

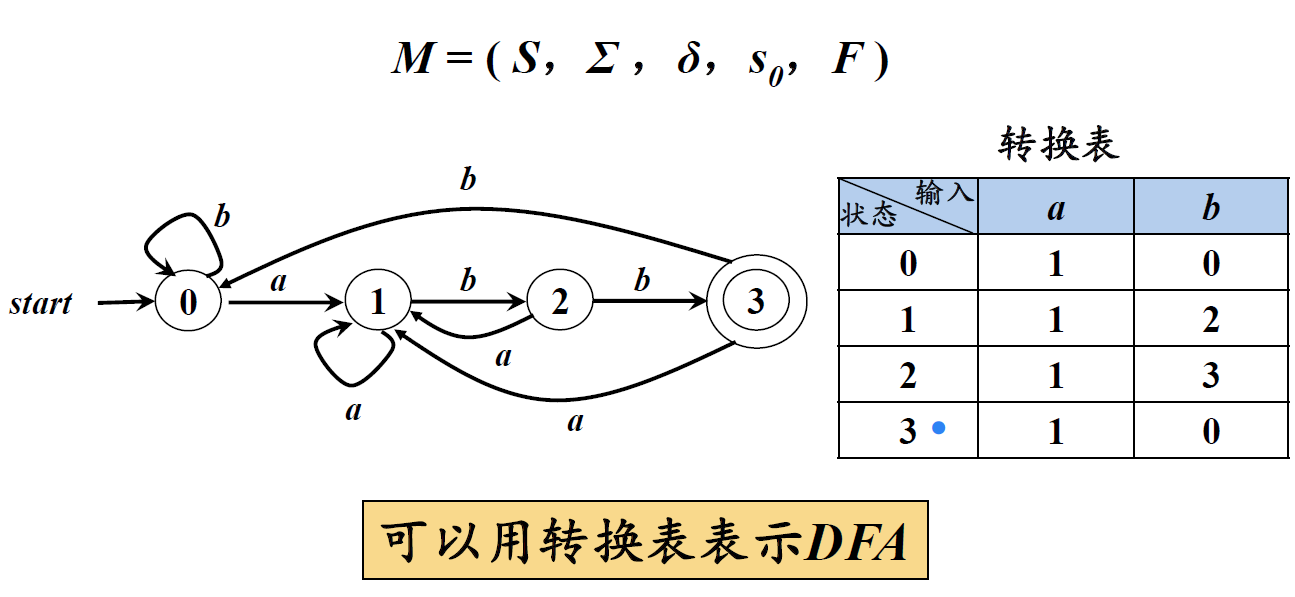
1、确定的有穷自动机DFA(Deterministic Finite Automata)

M = ( S，Σ ，δ，s0，F )

 S：有穷状态集
 Σ：输入字母表，即输入符号集合。假设ε不是 Σ中的元素
 δ：将S×Σ映射到S的转换函数。s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态。
 s0：开始状态 (或初始状态)，s0∈S
 F：接收状态（或终止状态）集合，F⊆ S

例如下图所展示的一个DFA

2、非确定的有穷自动机NFA(NonDeterministic Finite Automata)

M = ( S，Σ ，δ，s0，F )

 S：有穷状态集
 Σ：输入符号集合，即输入字母表。假设ε 不是Σ中的元素
 δ：将S×Σ映射到2S的转换函数。s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态集合
 s0：开始状态 (或初始状态)，s0∈S
 F：接收状态（或终止状态）集合，F⊆ S

例如下图所展示的一个NFA

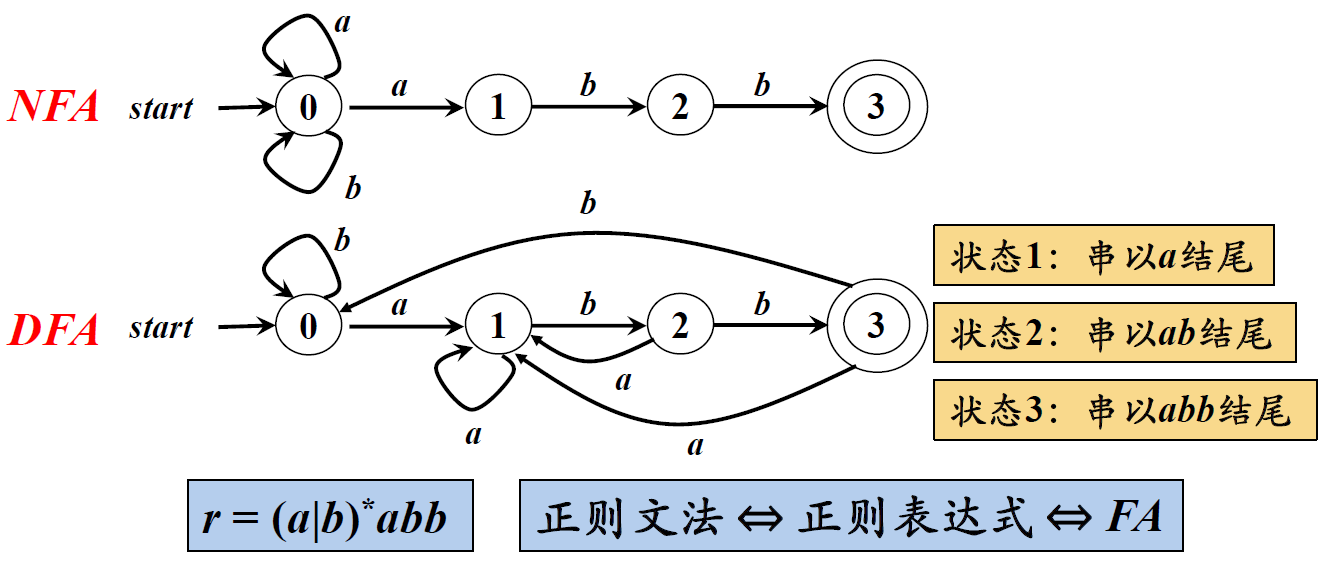
(DFA与NFA的区别在于：如上图用红色方框标出的位置，DFA的每一次输入只对应一个结果，而NFA的依次输入可能对应多个结果，形成一个结果集，后面将使用子集法将NFA构造为DFA)。

3、DFA和NFA的等价性

①

　　 对任何非确定的有穷自动机N ，存在定义同一语言的确定的有穷自动机D
　　 对任何确定的有穷自动机D ，存在定义同一语言的非确定的有穷自动机N

②

　　DFA和NFA可以识别相同的语言（如下图举例所示）

4、带有“ε-边”的NFA

M = ( S，Σ ，δ，s0，F )

 S：有穷状态集
 Σ：输入符号集合，即输入字母表。假设ε不是Σ中的元素
 δ：将S×(Σ∪{ε})映射到2S的转换函数。s∈S, a∈Σ∪{ε}, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态集合
 s0：开始状态 (或初始状态)，s0∈S
 F：接收状态（或终止状态）集合，F⊆ S

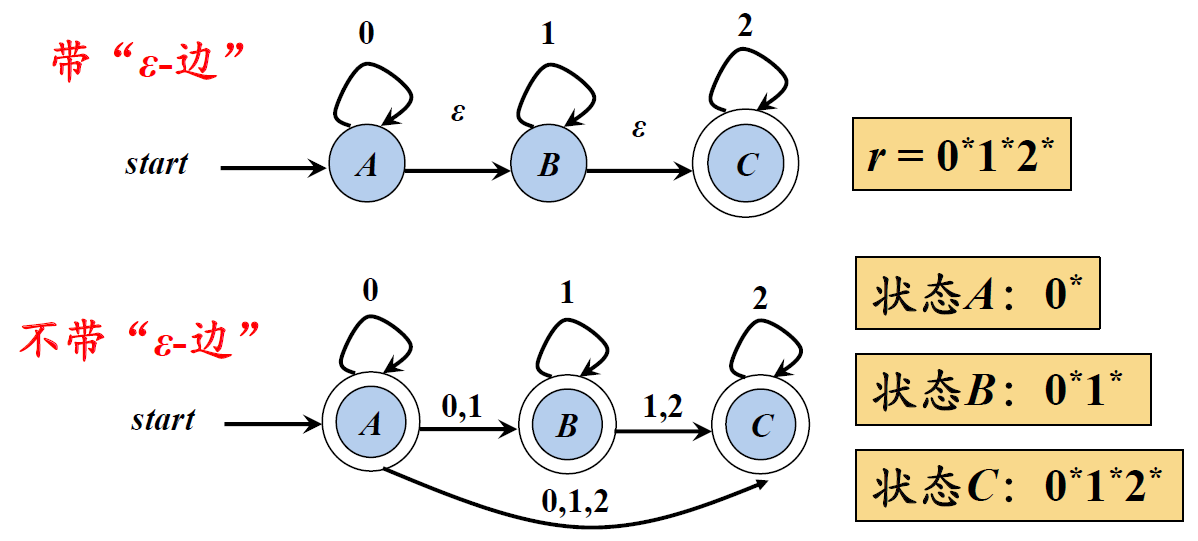
5、带有和不带有“ε-边”的NFA 的等价性

6、DFA的算法实现 

 输入：以文件结束符eof结尾的字符串x。DFA D 的开始状态s0，接收状态集 F，转换函数move。

 输出：如果 D接收 x，则回答“yes”，否则回答“no”。

 方法：将下述算法应用于输入串 x。

s = s0 ;
c = nextChar（）;
while（c! = eof ）｛
    s = move ( s , c ) ;
    c = nextChar ( ) ;
｝
if (s在F中) return“yes”;
else return “no”;

 函数nextChar( )返回输入串x的下一个符号

 函数move(s, c)表示从状态s出发，沿着标记为c的边所能到达的状态

三、【 从正则表达式到有穷自动机 】

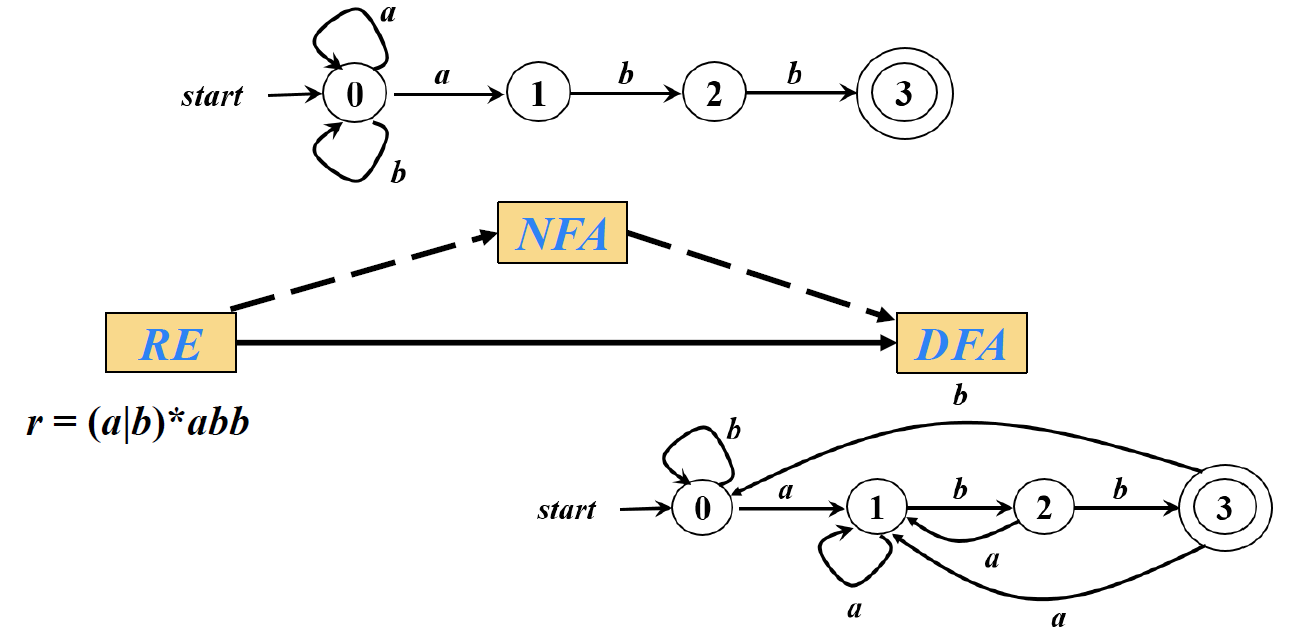
根据RE 构造NFA

□ ε对应的NFA

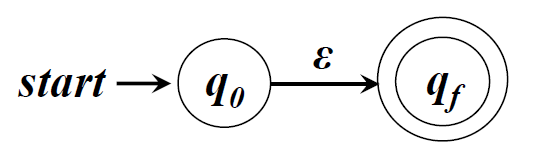
□ 字母表Σ中符号a对应的NFA

□ r = r₁r₂对应的NFA

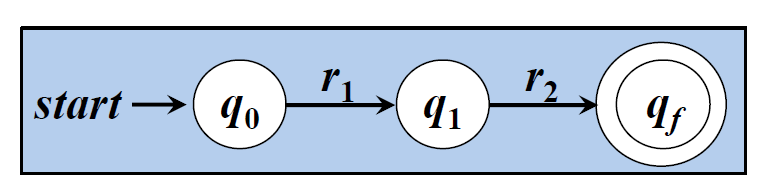
□ r = r₁|r₂对应的NFA

□ r = (r₁)*对应的NFA

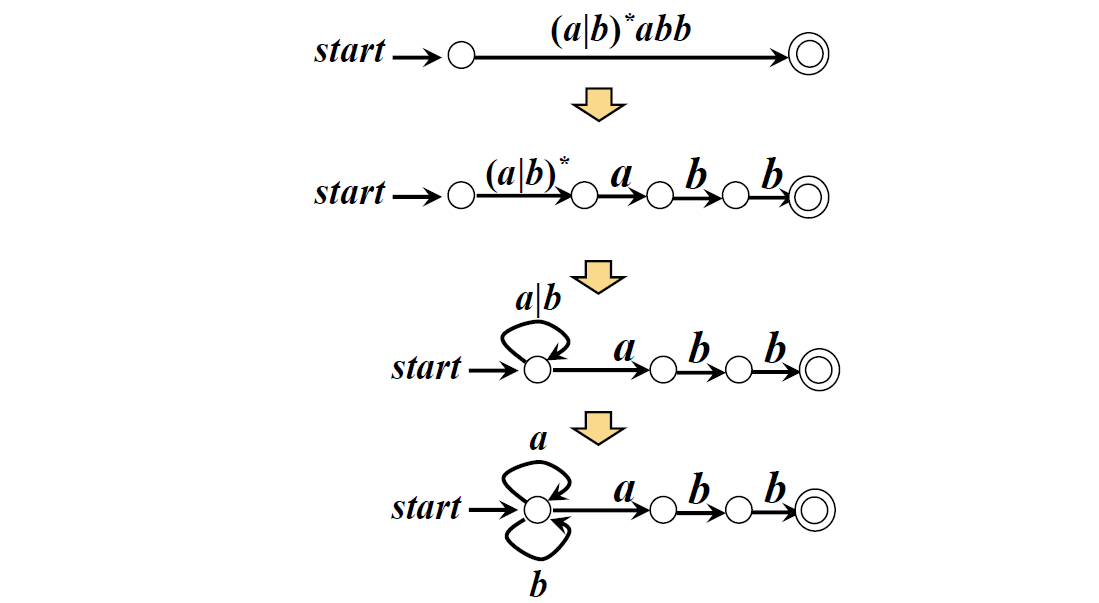
例:r=(a|b)*abb 对应的NFA