KinectFusion 介绍

KinectFusion简介

KinectFusion是微软在2011年发表的一篇论文里提到的点云重建的方法，论文题目是：KinectFusion: Real-Time Dense Surface Mapping and Tracking。点云是用Kinect采集的，然后算法把这些点云注册对齐，融合成一个整体点云。

Kinect是一个RGBD扫描仪，它可以同时采集彩色图像和深度图像。这是第一代Kinect和第二代Kinect的外观比较。

Kienct每秒可以获取30帧的RGBD图像，光线暗的情况下帧率会下降一些。

这是一个典型的KinectV2的数据。左边是带颜色的点云，右边的点云去掉了颜色，并且计算了法线信息。KinectFusion处理的是深度数据，像右边这种没有带颜色的点云。Kinect数据的详细介绍可以参考专题 Kinect数据

KinectFusion的核心有两个技术，一个是ICP注册，一个是符号距离函数。它的思路是一边注册，一边融合。由于是深度视频，帧与帧之间的位置差别不大，点云可以看作是初始注册好的，所以可以直接应用ICP进行精细注册。融合采用了符号距离函数技术，它在空间中定义了一个曲面的距离场，0等值面则为测量的曲面。

KinectFusion算法

下面介绍一下KinectFusion的算法步骤：

1. 生成三维点云：Kinect采集的原始数据是深度图像，可以用KinectSDK把深度图像转化为三维点云。

2. 点云预处理：预处理包含很多可选的算子，比如法线计算，点云范围裁剪（有些扫描仪在一定范围内的误差是可以接受的，故可以剔除掉误差范围大的区域），去噪（低精度的扫描数据可以去噪提高注册稳定性），边界点剔除（边界点的误差通常很大），孤立项剔除（孤立项的误差通常也很大）等。

3. 点云位姿估计：KinectFusion是一边注册，一边融合，所以它会维护一个当前融合的整体点云，记为PointCloud。新扫描的点云Depth，就是与PointCloud进行ICP注册。ICP注册的详细介绍可以参考专题点云ICP注册。

4. 点云融合：Depth与PointCloud注册好以后，它会与PointCloud再进行融合，更新PointCloud。

5. 整个扫描过程，每帧的点云重复步骤1-4，最后就得到一个整体点云PointCloud。

符号距离场函数(Signed Distance Function)

符号距离场函数，简称SDF，源自1996的一篇Siggraph论文：A volumetric method for building complex models from range images

SDF是定义在三维空间中的一个函数，它度量了空间点到曲面的距离。距离为0的点即为曲面上的点。我们把SDF离散化，定义在空间体素上。每个体素有三个变量：D，W，Flag。其中D为体素到曲面的距离值，W是权重，Flag是体素是否有效。

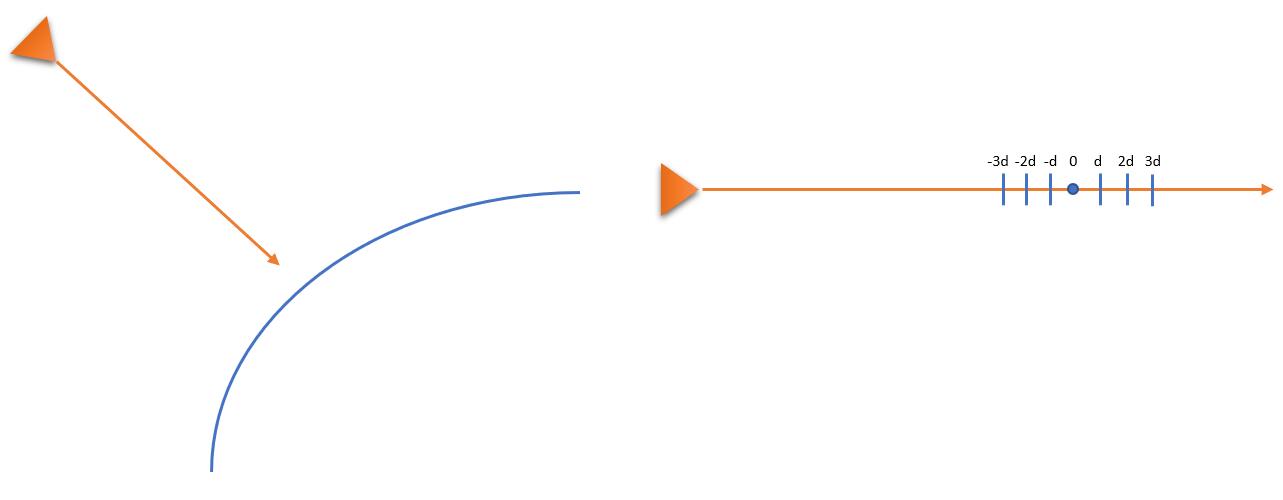
下面介绍点云如何融入SDF：点云是相机在某个视角下观察采集到的，如左图所示。单从一个视线观测一点来分析，如右图所示，这个视线上的点到曲面的距离可以定义如下，视线方向上，观测点前面的距离为负，观测点后面的距离为正。由于SDF是定义在空间中的体素里，我们这里也把距离离散化到体素里，其中d是体素宽度。由于系统误差的存在，我们给这些体素值一个权重，越靠近点云的体素权重越大。

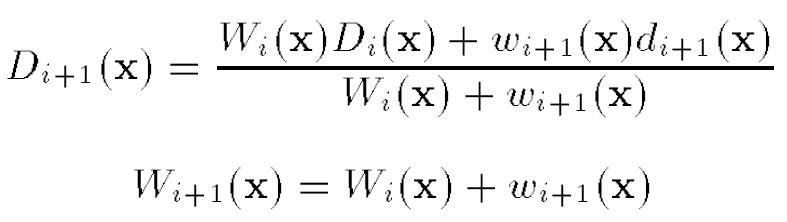
点云注册后，不断的往SDF里进行融合更新，最后把SDF的0等值面提取出来，就是融合的点云了。

SDF把点云通过距离函数的形式，离散化到空间体素里。而它的精髓在于给距离函数定义了一个范围，这个范围使得距离函数有了一定程度的光滑性。因为Kinect数据精度是很低的，两次观测的点云，会有很大的误差，如图所示。多个点云融合在一起，如何达到平均的效果，就是通过平均距离函数来实现的。我们知道，光滑函数的叠加，也是一个光滑函数。所以，每个距离函数光滑化以后，使得融合后的距离函数也是光滑的。而这个光滑性，就使得融合点云是光滑的，并且一定程度上能消掉点云重影。

KinectFusion算法分析

下面点评一下KinectFusion算法：

KienctFusion属于SLAM前端，高质量的点云重建还需要加入后端全局优化
KienctFusion注册时采用了Frame-to-Model的方式，也就是采集的点云与SDF融合的点云进行注册。有时候也可以用Frame-to-Frame的方式，也就是点云与前帧点云进行注册。这样速度可以更快一些。
点云注册只应用了深度图像，这个算是一个优点，比如有些场景下只有深度数据。有些时候，扫描对象的几何特征不明显，如果能借助彩色图像的辅助，点云注册可以更加的稳定。
点云融合的时候，KinectFusion采用了SDF技术，它擅长融合低精度数据，但是开销还是比较大的。可以采用一些性能高的融合方法来替换SDF。
原论文里面采用了GPU加速来达到实时。根据现在的CPU性能，其实是不用GPU辅助就能达到实时的。
KinectFusion算是三维SLAM前端的一个开始，之后出现了大量的三维SLAM前端方案，都是解决一些实际的问题，比如采集数据的质量差；扫描对象的特征不明显，这个特征包括几何特征和颜色特征；大数据量导致的质量和性能的平衡；多传感器的融合；面向移动设备的处理等。

有兴趣的读者，欢迎参考视频版本