[CSP-S模拟测试]:骆驼（模拟+构造）

题目描述

　　我们都熟悉走马步，现在我们定义一种新的移动方式——骆驼步，它在一个国际棋盘上的移动规则是这样的。

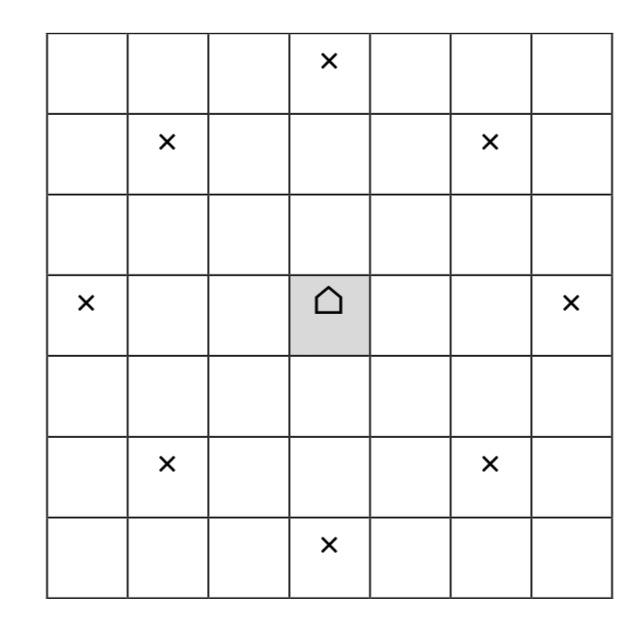
　　以看出，骆驼步可以向八个方向走动，且不能走出棋盘范围。
　　现在给出一个$N\times N$的棋盘，其中$N$是$5$的倍数。你需要从左上角出发，每步按照骆驼步的规则，经过每个格子恰好一次，且当你走了$N^2-1$步后，你离起点恰好只有一步的距离。
　　请给出一种合法的方案。

---

输入格式

第一行有一个整数$N$，表示$N\times N$的棋盘

---

输出格式

如果无解，输出$"impossible"$
否则，你输出一个$N\times N$的矩阵，其中$a_{i,j}$表示$(i,j)$是你经过的第$a_{i,j}$个格子。

---

样例

样例输入：

10

样例输出：

1 52 29 8 51 28 9 50 37 16
85 95 59 86 94 66 87 93 65 88
40 19 100 39 18 76 38 17 77 49
2 53 30 7 58 27 10 89 36 15
84 96 60 75 99 67 72 92 64 71
41 20 82 44 23 90 45 24 78 48
3 54 31 6 57 26 11 68 35 14
83 97 61 74 98 62 73 91 63 70
42 21 81 43 22 80 46 25 79 47
4 55 32 5 56 33 12 69 34 13

---

数据范围与提示

对于所有数据，保证$N\leqslant 1,000$且$N$是$5$的倍数。
其中一个数据点$N=5$，占$20$分，剩余$16$个数据点，每个$5$分。

---

题解

$N$是$5$的倍数无形中提示着我们不可能有$"impossible"$的数据点。

其中一个数据点$N=5$又提示着我们从这里入手。

事实证明，在一个$5\times 5$的格子里，从一个格子出发能终点可以是任意一个格子，那么可以考虑先预处理出来一些$5\times 5$的走法，然后拼接起来。

那么这时候分为两种情况：

　　$\alpha.N$是奇数。

　　$\beta.N$是偶数。

对于情况$\alpha$有这样一个构造方案：

上图中白点为总的起点，灰点表示每一个$5\times 5$的格子的起点，蓝点表示终点，黄点和红点分别表示最后两步。

对于情况$\beta$有这样一个构造方案：

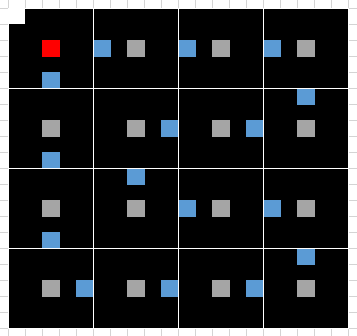
上图中白点为总的起点，灰点表示每一个$5\times 5$的格子的起点，蓝点表示终点，红点表示最后一步。

这样为题就简单多了，我们需要预处理七种$5\times 5$的格子，然后按照如上方案构造即可。

注意$N=5$需要特判

时间复杂度：$\Theta(n^2)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n;
int Map[1001][1001],t;
int base1[6][6]={0,0,0,0,0,0,0,1,6,11,-1,5,0,9,15,3,8,16,0,12,21,18,13,22,0,2,7,10,-1,4,0,19,14,23,20,17};
int base2[6][6]={0,0,0,0,0,0,0,10,21,6,9,22,0,16,13,24,19,14,0,5,8,1,4,7,0,11,20,15,12,23,0,17,3,25,18,2};
int base3[6][6]={0,0,0,0,0,0,0,18,10,24,17,9,0,13,21,7,12,22,0,5,16,1,4,25,0,19,11,23,20,8,0,14,3,6,15,2};
int base4[6][6]={0,0,0,0,0,0,0,21,10,25,22,9,0,15,18,7,12,17,0,5,23,1,4,24,0,20,11,16,19,8,0,14,3,6,13,2};
int base5[6][6]={0,0,0,0,0,0,0,18,5,24,19,6,0,10,21,16,9,22,0,25,13,1,4,14,0,17,8,23,20,7,0,11,3,15,12,2};
int base6[6][6]={0,0,0,0,0,0,0,25,17,7,24,16,0,12,4,21,13,5,0,19,9,1,18,8,0,22,14,6,23,15,0,11,3,20,10,2};
int base7[6][6]={0,0,0,0,0,0,0,1,6,13,21,5,0,11,19,3,8,18,0,14,22,-1,15,23,0,2,7,12,20,4,0,10,16,24,9,17};
void up(int x,int y)
{
	x--;y--;
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[x*5+i][y*5+j]=base4[i][j]+t;
	t+=25;
}
void down(int x,int y)
{
	x--;y--;
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[x*5+i][y*5+j]=base2[i][j]+t;
	t+=25;
}
void right(int x,int y)
{
	x--;y--;
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[x*5+i][y*5+j]=base3[i][j]+t;
	t+=25;
}
void left(int x,int y)
{
	x--;y--;
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[x*5+i][y*5+j]=base5[i][j]+t;
	t+=25;
}
void work1()
{
	t=23;
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[i][j]=base1[i][j];
	Map[4][4]=n*n-1;
	Map[1][4]=n*n;
	for(int i=2;i<n/5;i++)down(i,1);
	right(n/5,1);
	for(int i=n/5;i>2;i--)
	{
		if(i&1)
		{
			for(int j=2;j<n/5;j++)right(i,j);
			up(i,n/5);
		}
		else
		{
			for(int j=n/5;j>2;j--)left(i,j);
			up(i,2);
		}
	}
	for(int i=n/5;i>2;i--)
	{
		if(i&1)
		{
			up(2,i);
			left(1,i);
		}
		else
		{
			down(1,i);
			left(2,i);
		}
	}
	down(1,2);
	for(int i=6;i<=10;i++)
		for(int j=6;j<=10;j++)
			Map[i][j]=base6[i-5][j-5]+t;
}
void work2()
{
	for(int i=1;i<=5;i++)
		for(int j=1;j<=5;j++)
			Map[i][j]=base7[i][j];
	Map[3][3]=n*n;t=24;
	for(int i=2;i<n/5;i++)down(i,1);
	right(n/5,1);
	for(int i=n/5;i>=2;i--)
	{
		for(int j=2;j<n/5;j++)right(i,j);
		up(i,n/5);
		i--;
		for(int j=n/5;j>=3;j--)left(i,j);
		up(i,2);
	}
	t-=25;left(1,2);
}
int main()
{
	scanf("%d",&n);
	if(n==5){puts("1 9 19 2 10\n14 22 5 13 21\n7 17 25 8 18\n4 12 20 3 11\n15 23 6 16 24");return 0;}
	if(n&1)work1();
	else work2();
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
			printf("%d ",Map[i][j]);
		puts("");
	}
	return 0;
}

---

rp++