NOIp 图论算法专题总结 (3)：网络流 & 二分图 简明讲义

系列索引：

• NOIp 图论算法专题总结 (1)
• NOIp 图论算法专题总结 (2)
• NOIp 图论算法专题总结 (3)

网络流

概念 1

容量网络（capacity network）是一个有向图，图的边 \((u, v)\) 有非负的权 \(c(u, v)\)，被称为容量（capacity）。

图中有一个被称为源（source）的节点和一个被称为汇（sink）的节点。图中每条边称为弧（arc）。

实际通过每条边的流量记为 \(f(u, v)\)。

残量网络（residual network）是一个结构和容量网络相同的有向图，只不过边的权值为 \(c(u, v) - f(u, v)\)。

所有边上的流量集合被称为网络流（flow network）。

可行流的性质：

• 容量限制（Capacity constraints）：对任意 \(u,v∈V\)，\(0\le f(u,v)\le c(u,v).\)

• 流量守恒（Flow conservation）：对于任意非源汇节点 \(u∈V\)，满足 \(\sum_{(u,v)\in E} f(u,v)=\sum_{(v,u)\in E} f(v,u).\)

• 斜对称性（Skew symmetry）：对任意 \(u,v∈V\)，\(f(u,v)=-f(v,u).\)

最大流

增广路定理：网络达到最大流，当且仅当残留网络中没有增广路。

什么是增广路？

度娘百科：若 P 是图 G 中一条联通两个未匹配顶点的路径，且属于 M 的边和不属于 M 的边在 P 上交替出现，则称 P 为相对于 M 的一条增广路径（augmenting path）。（二分图的概念）

Ford–Fulkerson 方法：

本质：贪心！

首先，假如所有边上的流量都没有超过容量 (不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。一个最简单的例子就是，零流，即所有的流量都是 0 的流。

我们就从这个零流开始考虑，假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量严格 < 容量。那么，我们一定能找到这条路上的每一段的 (容量 – 流量) 的值当中的最小值 Δ。我们把这条路上每一段的流量都加上这个 Δ，一定可以保证这个流依然是可行流，这是显然的。

这样我们就得到了一个更大的流，它的流量是之前的流量 +Δ，而这条路就叫做增广路。

我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。

寻找增广路的时候我们可以简单的从源点开始做 BFS，并不断修改这条路上的 Δ 量，直到找到源点或者找不到增广路。

– nano9th

Edmonds-Karp 算法：

每次增广先在残量网络上找到一条增广路，然后将这条路上每条边的边权减去增广路上边权最小边的边权。再在该边的反向边上加上这个权值（用于撤消增广操作）。

时间复杂度 \(O(VE^2)\)。

建图：为了方便求取反向边，把一对互为反向边的边建在一起。

int pre[N], id[N]; // pre 标记上一个点，id 标记上一条边
bool v[N];

inline bool bfs() { // 寻找增广路
	memset(v, 0, sizeof v);
	queue<int> q;
	v[s]=true; q.push(s);
	while (!q.empty()) {
		int x=q.front(); q.pop();
		for (int i=head[x]; i; i=nex[i]) if (!v[to[i]] && w[i]) {
			pre[to[i]]=x, id[to[i]]=i, v[to[i]]=true;
			if (to[i]==t) return true;
			q.push(to[i]);
		}
	}
	return false;
}

inline int ek() {
	int res=0;
	while (bfs()) {
		int path=inf; // flow 为新的增广路
		for (int i=t; i!=s; i=pre[i]) path=min(path, w[id[i]]);
		for (int i=t; i!=s; i=pre[i]) w[id[i]]-=path, w[id[i]^1]+=path; // 正向边减、反向边加
		res+=path;
	}
	return res;
}

head[0]=1; // 直接从 2 开始计数，保证正反向边快速访问
add(a,b,c), add(b,a,0); // 添加反向边

Dinic 算法：

每次都走最短的增广路，并且每次增广允许多条增广路一起增广。

采用分层图（level graph）。对于每一个点，我们根据从源点开始的 BFS 序列，为每一个点分配一个深度，然后我们进行若干遍 DFS 寻找增广路，每一次由 \(u\) 推出 \(v\) 必须保证 \(v\) 的深度必须是 \(u\) 的深度 \(+ 1\)。

时间复杂度最坏 \(O(V^2E)\)。

显然，每次寻找增广路都要重复访问先前已查找过的边，可以优化。

当前弧优化：存储下以 \(u\) 开头的节点的当前弧 \(\text{cur}[u]\)，之后遇到 \(u\) 直接从 \(\text{cur}[u]\) 这条弧之后开始寻找，而不必再从 \(\text{head}[u]\) 开始。

int dep[N], cur[N];

inline bool bfs() { // 分层图
    memset(dep, 0, sizeof dep);
    queue<int> q;
    dep[s]=1; q.push(s);
    while (!q.empty()) {
        int x=q.front(); q.pop();
        for (int i=head[x]; i; i=nex[i])
            if (w[i]>0 && !dep[to[i]]) // 若该残量不为 0，且 to[i] 还未分配深度，则给其分配深度并放入队列
                dep[to[i]]=dep[x]+1, q.push(to[i]);
    }
    // 当汇点的深度不存在时，说明不存在分层图，同时也说明不存在增广路
    if (!dep[t]) return false; else return true;
}

int dfs(int x, int dis) { // 寻找增广路
    if (x==t) return dis;
    for (int& i=cur[x]; i; i=nex[i]) // cur[x] 记录当前弧
        if (dep[to[i]]==dep[x]+1 && w[i]) { // 分层图、残量不为 0
            int d=dfs(to[i], min(dis, w[i]));
            if (d>0) {w[i]-=d, w[i^1]+=d; return d; }
        }
    return 0; // 没有增广路
}

inline int dinic() {
    int res=0, d;
    while (bfs(s, t)) {
        for (int i=1; i<=n; i++) cur[i]=head[i]; // 重置当前弧
        while (d=dfs(s, inf)) res+=d;
    }
    return res;
}

head[0]=1; // 直接从 2 开始计数，保证正反向边快速访问
add(a,b,c), add(b,a,0); // 添加反向边

ISAP 算法：

基于分层思想，在每次增广完成后自动更新每个点所在的层。

时间复杂度 \(O(V^2E)\)。

实现略。 （其实是还不会）

最小割

一个网络的割（cut） 是这样一个边集，如果把这个集合的边删去，这个网络就不再连通。

这个边集中边的容量和被称为割的容量。容量最小的割被称为最小割（minimum cut）。

最大流最小割定理：对于一个容量网络，其最大流等于最小割的容量。

最小割在数值上等于最大流。

应用

点最大容量限制：

拆点，将一个点 \(u\) 拆成入点 \(u_{in}\) 和出点 \(u_{out}\) 两个，将所有指向 \(u\) 的边连接到 \(u_{in}\)，容量不变，从 \(u\) 连出的边改为从 \(u_{out}\) 连出，容量不变；最后再从 \(u_{in}\) 向 \(u_{out}\) 连接一条容量为 \(u\) 容量限制的边。

求多个（不重复）最长不下降子序列：

DP 求最长不下降子序列长度 \(s\)。

拆点。每个点向比它大 \(1\) 的点连一条容量为 \(1\) 的边。\(S\) 向 \(dp[1]\) 连一条容量为 \(1\) 的边，\(dp[s]\) 向 \(T\) 连一条容量为 \(1\) 的边。求最大流。

二分图匹配：

将原二分图的边的容量设为 \(1\)，\(S\) 向左部的节点连一条容量为 \(1\) 的边，右部的节点向 \(T\) 连一条容量为 \(1\) 的边。

如果二分图的一条边在匹配中，那么两个点对应的 \(S\) 和 \(T\) 的边一定满流，不可能再被匹配。

费用流

最小费用最大流：

每次在找增广路的时候都找费用最小的增广路；利用 SPFA 算法来寻找，边权就是费用。

int head[N], nex[M], to[M], w[M], c[M];
int d[N], f[N], pre[N], id[N]; // pre 标记上一个点，id 标记上一条边
bool inq[N];

inline void add(int x, int y, int z, int zz) {
	nex[++head[0]]=head[x], head[x]=head[0], to[head[0]]=y;
	w[head[0]]=z, c[head[0]]=zz;
}

inline bool spfa() { // 寻找增广路
	memset(d, 0x3f, sizeof d);
	memset(f, 0x3f, sizeof f);
	memset(inq, false, sizeof inq);
	queue<int> q;
	q.push(s), d[s]=0, inq[s]=true;
	while (!q.empty()) {
		int x=q.front(); q.pop(); inq[x]=false;
		for (int i=head[x]; i; i=nex[i])
			if (w[i] && d[to[i]]>d[x]+c[i]) {
				d[to[i]]=d[x]+c[i];
				f[to[i]]=min(w[i], f[x]);
				pre[to[i]]=x, id[to[i]]=i;
				if (!inq[to[i]]) q.push(to[i]), inq[to[i]]=true;
			}
	}
	return f[t]!=f[s];
}

inline void mcmf() {
	int flow=0, cost=0;
	while (spfa()) {
		for (int i=t; i!=s; i=pre[i]) w[id[i]]-=f[t], w[id[i]^1]+=f[t];
		flow += f[t], cost += f[t] * d[t];
	}
	printf("%d %d\n", flow, cost);
}

head[0]=1;
add(a, b, aa, bb), add(b, a, 0, -bb);

众所周知：

NOI2018 D1T1 出题人：“SPFA 它死了！”

考虑使用 Dijkstra 替换 SPFA。

如何实现负权边？暴力加上一个值！（爆 long long）

给每个点定义一个势 \(h\)，将转移从 \(d(u)=d(v)+w\) 改成 \(d(u)=d(v)+w+h(v)−h(u)\)，并保证 \(w+h(v)−h(u)≥0\)。参见 Link 。

概念 2

点覆盖集（vertex cover）是无向图的一个点集，使得该图中的所有边至少有一个端点在该集合内。

点数最少的点覆盖集被称为最小点覆盖集。

点独立集（independent set）是无向图的一个点集，使得该集合中任意两个点之间不连通。

点数最多的点被称为最大点独立集。

引理：

最小点覆盖集 \(=\) 最大匹配 \(= V -\) 最大点独立集 \(= V -\) 最小边覆盖。

最大点权独立集 \(= \sum \textrm{val}(x) -\) 最小点权覆盖集。

最小点权覆盖集 \(=\) 最小割。

最大点权闭合子图 \(= \sum \{\textrm{val}(x)| \textrm{val}(x)>0\} -\) 最小割

二分图

概念

什么是二分图（bipartite graph）？

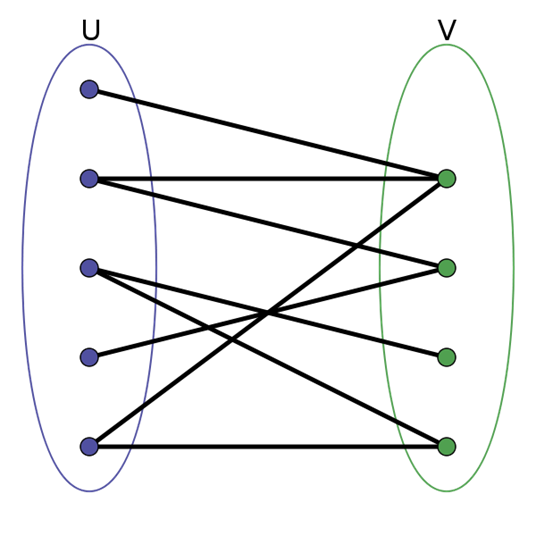
性质：不存在节点个数为奇数的环。

二分图染色

二分图染色（判断是否二分图）：

int col[N]; bool v[N];

bool dfs(int x) {
    v[x] = true;
    for (int i=head[x]; i; i=nex[i]) {
        if (!v[to[i]]) {
            col[to[i]] = col[x] ^ 1;
            if (!dfs(to[i])) return false;
        } else if (col[x]==col[to[i]]) return false;
    }
    return true;
}

int flag = true;
for (int i=1; i<=n; i++) if (!v[i] && !dfs(i)) {
    flag = false; break;
}
if (flag) printf("Yes\n"); else printf("No\n");

二分图匹配

二分图的匹配（matching）是一些边，要求满足每个节点最多只被这些边里面的一条边覆盖。

所有匹配中，边数最多的匹配被称为二分图的最大匹配。

匈牙利算法：

从二分图中找出一条增广路（augmenting path），让路径的起点和终点都是还没有匹配过的点，并且路径经过的连线是一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现。

找到这样的路径后，显然路径里没被匹配的连线比已经匹配了的连线多一条，于是修改匹配图，把路径里所有匹配过的连线去掉匹配关系，把没有匹配的连线变成匹配的，这样匹配数就比原来多 \(1\) 个。

不断执行上述操作，直到找不到这样的路径为止。

时间复杂度 \(O(VE)\)。

int mat[N], v[N], cnt;  // N 为左子图的大小，v 为时间戳

bool hungary(int x, int vt) {
	for (register int i=head[x]; i; i=nex[i]) if (v[to[i]]<vt) {
		v[to[i]]=vt;
		if (!mat[to[i]] || hungary(mat[to[i]], vt)) {
			mat[to[i]]=x; return true;
		}
	}
	return false;
}

for (int i=1; i<=n; ++i) if (hungary(i, i)) ++cnt;

网络流解二分图匹配：参见上面 [[网络流]] 部分。