[CSP-S模拟测试]:字符（模拟+剪枝）

题目传送门（内部题33）

---

输入格式

第一行，两个整数$T,C$，表示测试数据组数和字符种类数。
对于每组数据：第一行，一个正整数$M$；接下来的$M$行，每行两个整数$P_k,X_k$（$S$的下标从$1$起），保证不会出现$P_{k_1}=P_{k_2}$且$X_{k_1}\neq X_{k_2}$的情况。

---

输出格式

对于每组数据输出一行，若无解则输出$NO$，若有解则输出对应的$a_0,a_1,...,a_{C−1}$（用空格隔开）。

---

样例

样例输入：

2 3
3
2 0
3 1
5 2
4
1 0
2 2
3 1
4 2

样例输出：

2 1 2
NO

---

数据范围与提示

样例解释：

对于第一组数据，可能的答案有$S=0011200112···$和$S=0012200122···$，
分别对应$a_0=2,a_1=2,a_2=1$和$a_0=2,a_1=1,a_2=2$，后者$a$的字典序更小。

数据范围：

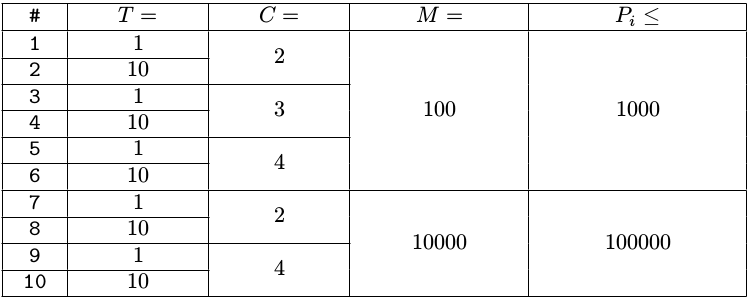
对于所有数据，$1\leqslant T\leqslant 5,2\leqslant C\leqslant 4,1\leqslant M\leqslant 10,000,1\leqslant P_i\leqslant 100,000,0\leqslant X_i<C−1$。

---

题解

又一次没有打正解。

首先，我们要暴力找到一组可行的$S$的长度，从小到大找，但是不要找到了就跳出，因为这样不一定最优。

正解好复杂的，我看不懂……

所以我们考虑剪枝，在我们判当前长度不可行的时候如果是因为$i<j,s_i>s_j$，那么以后肯定不会出现可行长度了，就可以直接输出当前最优答案。

时间复杂度：$\Theta(T\times \max(P_i)^2)$。

期望得分：$60$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int T,C,M,L,S[100010];
int ans[5],a[5],maxn;
pair<int,int> pos[100001];
pair<int,int> pre;
void pre_work()
{
	memset(ans,0x3f,sizeof(ans));
	L=0;
}
void check(int x)
{
	pre=make_pair(0,0);
	memset(S,0,sizeof(S));
	memset(a,0,sizeof(a));
	maxn=0;
	for(int i=1;i<=M;i++)
	{
		int flag=(pos[i].first-1)%x+1;
		if(S[flag]&&S[flag]!=pos[i].second)return;
		S[flag]=pos[i].second;
	}
	for(int i=1;i<=L;i++)
	{
		if(!S[i])continue;
		if(S[i]<maxn){L=0;return;}
		maxn=max(maxn,S[i]);
		a[S[i]]=max(a[S[i]],i);
	}
	a[C]=x;
	for(int i=1;i<=C;i++)
	{
		if(!a[i])a[i]=a[i-1]+1;
		if(a[i]<=a[i-1])return;
	}
	for(int i=C;i>=2;i--)a[i]=a[i]-a[i-1];
	for(int i=1;i<=C;i++)
	{
		if(a[i]>ans[i])return;
		else if(a[i]<ans[i])
		{
			for(int j=1;j<=C;j++)ans[j]=a[j];
			return;
		}
	}
}
int main()
{
	scanf("%d%d",&T,&C);
	while(T--)
	{
		pre_work();
		scanf("%d",&M);
		for(int i=1;i<=M;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			pos[i]=make_pair(x,y+1);
			L=max(L,x+C);
		}
		for(int i=C;i<=L;i++)check(i);
		if(ans[1]>1000000000)puts("NO");
		else{for(int i=1;i<=C;i++)printf("%d ",ans[i]);puts("");}
	}
	return 0;
}

---

rp++