R_Studio(癌症)数据连续属性离散化处理

　　

　　对“癌症.csv”中的肾细胞癌组织内微血管数进行连续属性的等宽离散化处理(分为3类)，并用宽值找替原来的值

　　癌症.csv

　　

setwd('D:\\data')

list.files()

dat=read.csv(file="癌症.csv",header=TRUE)

#等宽离散化
v1=ceiling(dat[,1])

#等频离散化
names(data)='f'#变量重命名
attach(dat)
seq(0,length(f),length(f)/2)#等频划分为6组
v=sort(f)#按大小排序作为离散化依据
v2=rep(0,26)#定义新变量
for(i in 1:26) v2[i]=ifelse(f[i]<=v[13],1,
                            ifelse(f[i]<=v[26],2)) 

detach(dat)

#聚类离散化
result=kmeans(dat[,4],2)
v3=result$cluster 

#图示结果
plot(dat[,4],v1,xlab='肾细胞癌组织内微血管数',ylab='等宽离散化')
plot(dat[,4],v2,xlab='肾细胞癌组织内微血管数',ylab='等频离散化')
plot(dat[,4],v3,xlab='肾细胞癌组织内微血管数',ylab='聚类离散化')

Gary.R

　　等宽离散化：将连续数据按照等宽区间标准离散化数据

　　

setwd('D:\\data')

list.files()

dat=read.csv(file="癌症.csv",header=TRUE)

#等宽离散化
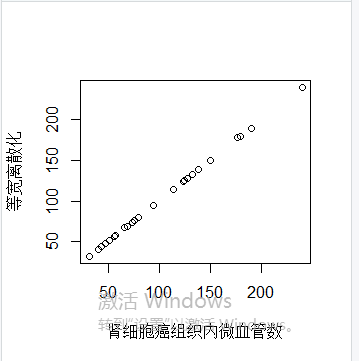
v1=ceiling(dat[,4])

#图示结果
plot(dat[,4],v1,xlab='肾细胞癌组织内微血管数',ylab="等宽离散化")

　　

　　等频离散化：将相同数量的数据放进一个区间

setwd('D:\\data')

list.files()

dat=read.csv(file="癌症.csv",header=TRUE)

#等频离散化
names(data)='f'#变量重命名
attach(dat)
seq(0,length(f),length(f)/2)#等频划分为6组
v=sort(f)#按大小排序作为离散化依据
v2=rep(0,26)#定义新变量
for(i in 1:26) v2[i]=ifelse(f[i]<=v[13],1,
                            ifelse(f[i]<=v[26],2)) 

#图示结果
plot(dat[,4],v2,xlab='肾细胞癌组织内微血管数',ylab="等频离散化")

　　

　　聚类离散化：一维聚类离散包括两个过程：通过聚类算法（K-Means算法）将连续属性值进行聚类，处理聚类之后的到的k个簇，得到每个簇对应的分类值（类似这个簇的标记）

setwd('D:\\data')

list.files()

dat=read.csv(file="癌症.csv",header=TRUE)

#聚类离散化
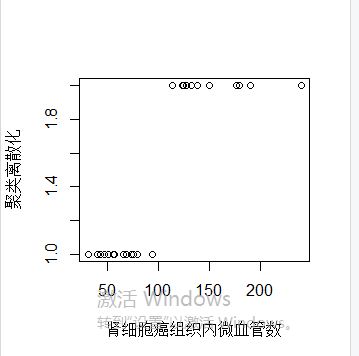
result=kmeans(dat[,4],2)
v3=result$cluster 

#图示结果
plot(dat[,4],v3,xlab='肾细胞癌组织内微血管数',ylab='聚类离散化')