[BZOJ 2989]数列(二进制分组+主席树)

[BZOJ 2989]数列(二进制分组+主席树)

题面

给定一个长度为n的正整数数列a[i]。

定义2个位置的graze值为两者位置差与数值差的和，即graze(x,y)=|x-y|+|a[x]-a[y]|。

2种操作（k都是正整数）：

1.Modify x k：将第x个数的值修改为k。

2.Query x k：询问有几个i满足graze(x,i)<=k。因为可持久化数据结构的流行，询问仅要考虑当前数列，还要考虑任意历史版本，即统计任意位置上出现过的任意数值与当前的a[x]的graze值<=k的对数。（某位置多次修改为同样的数值，按多次统计）

分析

预备知识

观察到\(|x-y|+|a[x]-a[y]|\),我们想到曼哈顿距离。于是我们把(x,a[x])看作一个二维平面上的点，而查询的是到平面上一定点距离<=k的点的个数。同时这样还避免了可持久化的问题，因为把a[x]修改成k，相当于新建了一个点。

到平面上一定点曼哈顿距离=k的点的集合（曼哈顿距离下的圆）是一个斜45°，边长为\(\frac{\sqrt{2}}{2}k\)的正方形。我们求的答案就是这个正方形里的点的个数

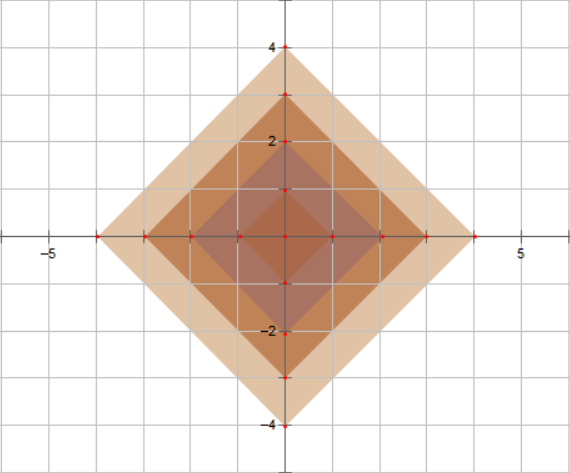
[图片转载自https://www.cnblogs.com/SGCollin/p/9636955.html]

这样的点距离不太好求。但是我们知道切比雪夫距离下的圆是一个四边都平行坐标轴的正方形。因此我们可以把曼哈顿距离转成对应的切比雪夫距离。注：\((x_1,y_1)和(x_2,y_2)的切比雪夫距离是max(|x_1-x_2|,|y_1-y_2|)\)

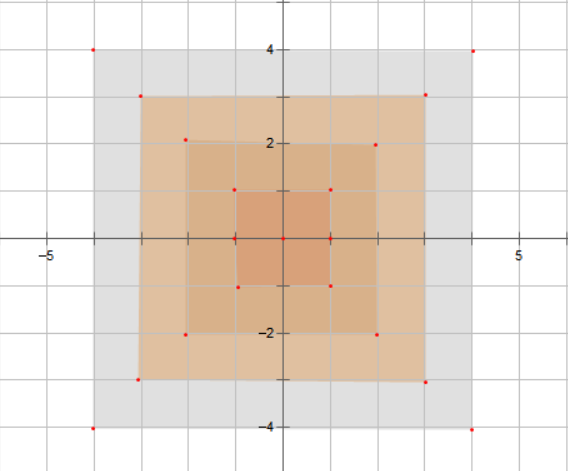
考虑把两个点转化成\((x_1+y_1,x_1-y_1),(x_2+y_2,x_2-y_2)\),容易发现新点的切比雪夫距离和原来点的曼哈顿距离相同.

那么我们只要把询问和修改的每个点都转成(x+y,x-y)的形式，然后问题就变成在把原来查询的正方形转换后新的正方形里点的个数。即查询(x-k,y-k)到(x+k,y+k)的二维前缀和

正文

当然可以离线cdq分治，方法见这篇博客。但是我们这里给出一个在线做法。

考虑没有修改的情况，把x坐标离散化，以x坐标为下标建n棵可持久化线段树维护前缀和，y坐标为线段树下标。在第x-k(离散化后)到第x+k棵线段树上查区间[y-k,y+k]就可以得到二维前缀和 .

有修改的情况下我们可以运用二进制分组的方法。

二进制分组的基本思想是把修改操作按二进制分组，遇到修改就在尾部加一个，并与之前的合并。因此，组数只有\(O(\log m)\)个

比如之前有23（16+4+2+1）个，加了1个后就变成16+4+2+1+1,把1和1合并变成 2,2和2合并...最后就变成了24(16+8),其中16对应的块存储前16组修改操作之后数据结构的状态。合并的时候暴力插入，然后重构合并块，相当于把原来的修改操作都撤销然后再加回去。

遇到查询就在每个组内查询，再加起来就好了。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<utility>
#include<vector>
#define maxn 100000
#define maxlogn 32
#define INF 0x3f3f3f3f
using namespace std;
int n,q;
int a[maxn+5];
struct mem_pool{//手写内存池，回收删除的点防止MLE
	 int top=0;
	 int stk[maxn*2*maxlogn+5];
	 inline void ini(int n){
	 	for(int i=n;i>=1;i--) stk[++top]=i;
	 }
	 inline int New(){
	 	return stk[top--];
	 }
	 inline void del(int x){
	 	stk[++top]=x;
	 }
}pool;

//把x坐标离散化，以x坐标为下标建n棵可持久化线段树维护前缀和，y坐标为线段树下标
//在第x-k(离散化后)到第x+k棵线段树上查区间[y-k,y+k]就可以得到二维前缀和
int root[maxlogn+5][maxn*2+5];//root[i][j],第i个分组区间里面第j小的x坐标对于的线段树
struct persist_segment_tree{
	#define lson(x) tree[x].ls
	#define rson(x) tree[x].rs
	struct node{
		int ls;
		int rs;
		int val;
	}tree[maxn*2*maxlogn+5];
	bool is_del[maxn*2*maxlogn+5];
	//因为一个点不能被删除两次(主席树上的一个点可能被多个节点指向)，打标记
	int New(){
		int x=pool.New();
		is_del[x]=0;
		return x;
	}
	void push_up(int x){
		tree[x].val=tree[lson(x)].val+tree[rson(x)].val;
	}
	void update(int &x,int last,int upos,int l,int r){
		x=New();
		tree[x]=tree[last];
		if(l==r){
			tree[x].val++;
			return;
		}
		int mid=(l+r)>>1;
		if(upos<=mid) update(tree[x].ls,tree[last].ls,upos,l,mid);
		else update(tree[x].rs,tree[last].rs,upos,mid+1,r);
		push_up(x);
	}
	int query(int xl,int xr,int ql,int qr,int l,int r){
		if(ql<=l&&qr>=r){
			return tree[xr].val-tree[xl].val;
		}
		int mid=(l+r)>>1;
		int ans=0;
		if(ql<=mid) ans+=query(tree[xl].ls,tree[xr].ls,ql,qr,l,mid);
		if(qr>mid) ans+=query(tree[xl].rs,tree[xr].rs,ql,qr,mid+1,r);
		return ans;
	}
	void del(int x){
		if(is_del[x]) return;
		is_del[x]=1;
		pool.del(x);
		if(tree[x].ls) del(tree[x].ls);
		if(tree[x].rs) del(tree[x].rs);
		tree[x].val=tree[x].ls=tree[x].rs=0;
	}
}T;

int top=0;
vector< pair<int,int> >v[maxlogn+5];//存储每个组里的修改操作
int sz[maxlogn+5];
void rebuild(int id){//重构某个组
	for(int i=1;i<=sz[id];i++){
		//把第i个y坐标更新
		T.update(root[id][i],root[id][i-1],v[id][i-1].second,1,maxn*2);
	}
}
void insert(pair<int,int> p){
	sz[++top]=1;
	v[top].push_back(p);
	rebuild(top);
	while(top>1&&sz[top-1]==sz[top]){//类似二进制加法进位，去合并
		for(int i=0;i<sz[top];i++) v[top-1].push_back(v[top][i]);
		sort(v[top-1].begin(),v[top-1].end());//排序，相当于离散化
		v[top].clear();
		for(int i=1;i<=sz[top];i++){
			if(root[top-1][i]) T.del(root[top-1][i]);//先删除，等下再暴力重构
			if(root[top][i]) T.del(root[top][i]);
		}
		sz[top-1]+=sz[top];
		rebuild(top-1);
		top--;
	}
}
int query(pair<int,int>p,int k){
	int x=p.first,y=p.second,l,r;
	int ans=0;
	for(int i=1;i<=top;i++){
		l=upper_bound(v[i].begin(),v[i].end(),make_pair(x-k,0))-v[i].begin();
		r=upper_bound(v[i].begin(),v[i].end(),make_pair(x+k,INF))-v[i].begin();
		if(l<=r) ans+=T.query(root[i][l],root[i][r],max(y-k,0),min(y+k,maxn*2),1,maxn*2);
	}
	return ans;
}

char s[10];
int main(){
	int x,k;
	scanf("%d %d",&n,&q);
	pool.ini(maxn*2*maxlogn);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		insert(make_pair(a[i]+i,a[i]-i+maxn));//为了防止负数，要+maxn，注意数组要开两倍
	}
	for(int i=1;i<=q;i++){
		scanf("%s",s);
		if(s[0]=='M'){
			scanf("%d %d",&x,&k);
			a[x]=k;
			insert(make_pair(a[x]+x,a[x]-x+maxn));
		}else{
			scanf("%d %d",&x,&k);
			printf("%d\n",query(make_pair(a[x]+x,a[x]-x+maxn),k));
		}
	}
}