【CF1257E】The Contest【线段树】

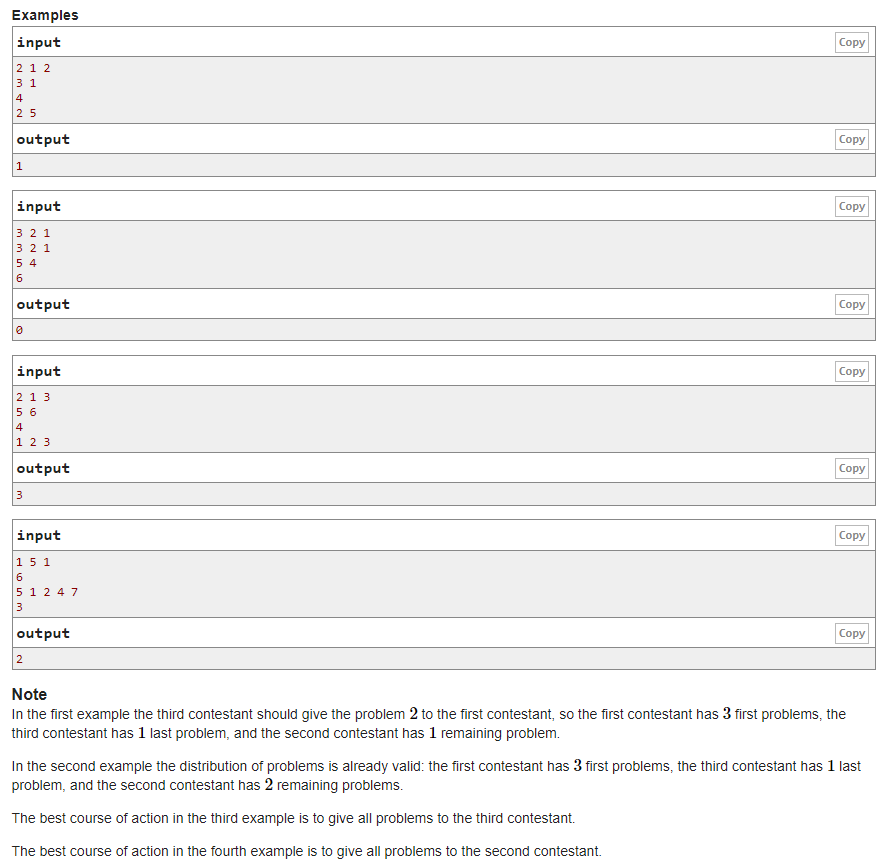
题意：给定三个序列abc，问最少操作几次使得满足a<b<c

题解：将三个序列合并起来，设cnt[i][1/2/3]表示前i个数有几个是来自序列1/2/3的。

枚举第一个序列要到i，此时对于第一个序列的操作次数就是cnt[i][2]+cnt[i][3]+cnt[n][1]-cnt[i][1]

对于第二个序列，暴力枚举要到j，此时的操作次数就是cnt[j][3]-cnt[i][3]+cnt[n][2]-cnt[j][2]

将两个加起来就是答案，求出最小的那个

显然这样做是O(n^2)的，考虑优化

可以观察到，对于一个确定的i，cnt[i][3]是定值，将式子改写为cnt[j][3]+cnt[n][2]-cnt[j][2]-cnt[i][3]，设f[i]=cnt[i][3]+cnt[n][2]-cnt[i][2]，那么f[i]是一个确定的函数，式子进一步改写为f[j]-cnt[i][3]

相当于对于每个i，求一个最小的f[j]-cnt[i][3]，用一个线段树即可

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;
int k1,k2,k3,a,n,ans=1e9;
int cnt[][];
struct node
{
    int v,bh;
}q[];
bool cmp(const node &T1,const node &T2){return T1.v<T2.v;}
class Segtree
{
public:
    int v[*],fl[*];

    void pushup(int fxy)
    {
      v[fxy]=min(v[fxy<<],v[fxy<<|]);
    }
    void pushdown(int fxy)
    {
      if(fl[fxy])
      {
        v[fxy<<]+=fl[fxy];
        v[fxy<<|]+=fl[fxy];
        fl[fxy<<]+=fl[fxy];
        fl[fxy<<|]+=fl[fxy];
        fl[fxy]=;
      }
    }
    void build(int l,int r,int fxy)
    {
      if(l==r)
      {
        v[fxy]=cnt[l][]+cnt[n][]-cnt[r][];
        return;
      }
      int mid=l+r>>;
      build(l,mid,fxy<<);
      build(mid+,r,fxy<<|);
      pushup(fxy);
    }
    void change(int l,int r,int al,int ar,int tv,int fxy)
    {
        if(l==al && r==ar)
        {
          v[fxy]+=tv;
          fl[fxy]+=tv;
          return;
        }
        pushdown(fxy);
        int mid=l+r>>;
        if(ar<=mid)change(l,mid,al,ar,tv,fxy<<);
        if(al>mid)change(mid+,r,al,ar,tv,fxy<<|);
        if(al<=mid && ar>mid)
        {
          change(l,mid,al,mid,tv,fxy<<);
          change(mid+,r,mid+,ar,tv,fxy<<|);
        }
        pushup(fxy);
    }
    int ask(int l,int r,int al,int ar,int fxy)
    {
        if(l==al && r==ar)return v[fxy];
        pushdown(fxy);
        int mid=l+r>>;
        if(ar<=mid)return ask(l,mid,al,ar,fxy<<);
        if(al>mid)return ask(mid+,r,al,ar,fxy<<|);
        return min(ask(l,mid,al,mid,fxy<<),ask(mid+,r,mid+,ar,fxy<<|));
    }
}segtree;
int main()
{
    scanf("%d%d%d",&k1,&k2,&k3);
    for(int i=;i<=k1;i++){scanf("%d",&a);q[i]=(node){a,};}
    for(int i=;i<=k2;i++){scanf("%d",&a);q[i+k1]=(node){a,};}
    for(int i=;i<=k3;i++){scanf("%d",&a);q[i+k1+k2]=(node){a,};}
    n=k1+k2+k3;
    sort(q+,q++n,cmp);
    for(int i=;i<=n;i++)
    {
      cnt[i][]=cnt[i-][]+(q[i].bh==);
      cnt[i][]=cnt[i-][]+(q[i].bh==);
      cnt[i][]=cnt[i-][]+(q[i].bh==);
    }
    int t;
    segtree.build(,n,);
    for(int i=;i<n;i++)
    {
      t=segtree.ask(,n,i+,n,);
      t=min(t,cnt[n][]-cnt[i][]);
      ans=min(ans,t+cnt[i][]+cnt[i][]+cnt[n][]-cnt[i][]);
      if(q[i+].bh==)segtree.change(,n,i+,n,-,);
    }
    ans=min(ans,cnt[n][]+cnt[n][]);
    printf("%d\n",ans);
    return ;
}