NOIp 2018 货币系统 贪心

题目描述

在网友的国度中共有 nnn 种不同面额的货币，第 iii 种货币的面额为 a[i]a[i]a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 nnn、面额数组为 a[1..n]a[1..n]a[1..n] 的货币系统记作 (n,a)(n,a)(n,a)。

在一个完善的货币系统中，每一个非负整数的金额 xxx 都应该可以被表示出，即对每一个非负整数 xxx，都存在 nnn 个非负整数 t[i]t[i]t[i] 满足 a[i]×t[i]a[i] \times t[i]a[i]×t[i] 的和为 xxx。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 xxx 不能被该货币系统表示出。例如在货币系统 n=3n=3n=3, a=[2,5,9]a=[2,5,9]a=[2,5,9] 中，金额 1,31,31,3 就无法被表示出来。

两个货币系统 (n,a)(n,a)(n,a) 和 (m,b)(m,b)(m,b) 是等价的，当且仅当对于任意非负整数 xxx，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)(m,b)(m,b)，满足 (m,b)(m,b)(m,b) 与原来的货币系统 (n,a)(n,a)(n,a) 等价，且 mmm 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 mmm。

输入输出格式

输入格式：

输入文件的第一行包含一个整数 TTT，表示数据的组数。

接下来按照如下格式分别给出 TTT 组数据。 每组数据的第一行包含一个正整数 nnn。接下来一行包含 nnn 个由空格隔开的正整数 a[i]a[i]a[i]。

输出格式：

输出文件共有 TTT 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a)(n,a)(n,a) 等价的货币系统 (m,b)(m,b)(m,b) 中，最小的 mmm。

输入输出样例

输入样例#1：
复制

2
4
3 19 10 6
5
11 29 13 19 17 

输出样例#1： 复制

2
5  

说明

在第一组数据中，货币系统 (2,[3,10])(2, [3,10])(2,[3,10]) 和给出的货币系统 (n,a)(n, a)(n,a) 等价，并可以验证不存在 m<2m < 2m<2 的等价的货币系统，因此答案为 222。 在第二组数据中，可以验证不存在 m<nm < nm<n 的等价的货币系统，因此答案为 555。

【数据范围与约定】

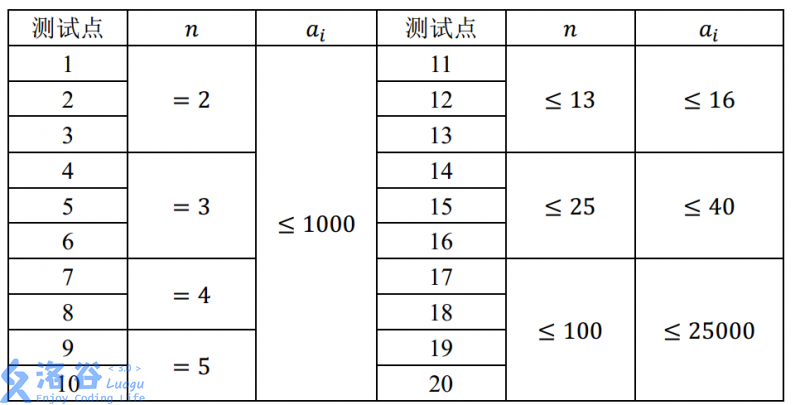
对于 100%100\%100% 的数据，满足 1≤T≤20,n,a[i]≥11 ≤ T ≤ 20, n,a[i] ≥ 11≤T≤20,n,a[i]≥1。

贪心地排序，那么问题就等价于如果大的数可以被小的数表示，那么就可以标记；

我们就可以用完全背包来做即可；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 400005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + ;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = ;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
    ll x = ;
    char c = getchar();
    bool f = false;
    while (!isdigit(c)) {
        if (c == '-') f = true;
        c = getchar();
    }
    while (isdigit(c)) {
        x = (x << ) + (x << ) + (c ^ );
        c = getchar();
    }
    return f ? -x : x;
}

ll gcd(ll a, ll b) {
    return b ==  ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1; y = 0; return a;
    }
    ans = exgcd(b, a%b, x, y);
    ll t = x; x = y; y = t - a / b * y;
    return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
    ll ans = ;
    a = a % c;
    while (b) {
        if (b % )ans = ans * a%c;
        b /= ; a = a * a%c;
    }
    return ans;
}

int T;
int n;
int a[maxn];
int Hash[maxn];

int main()
{
    //ios::sync_with_stdio(0);
    rdint(T);
    while (T--) {
        int ans = ;
        rdint(n); ms(a); ms(Hash);
        for (int i = ; i <= n; i++)rdint(a[i]);
        sort(a + , a +  + n);
        Hash[] = ;
        for (int i = ; i <= n; i++) {
            if (!Hash[a[i]])ans++;
            for (int j = a[i]; j <= ; j++)if (Hash[j - a[i]])Hash[j] = ;
        }
        cout << ans << endl;
    }
    return ;
}