P4345 [SHOI2015]超能粒子炮·改 Lucas

\(\color{#0066ff}{ 题目描述 }\)

曾经发明了脑洞治疗仪与超能粒子炮的发明家 SHTSC 又公开了他的新发明：超能粒子炮・改——一种可以发射威力更加强大的粒子流的神秘装置。

超能粒子炮・改相比超能粒子炮，在威力上有了本质的提升。它有两个参数\(n\),\(k\)，它会向每个编号为\(0\)到\(k\)（包含两端）的位置\(i\)发射威力为\(C_{n}^{i} mod 2333\)的粒子流。

现在 SHTSC 给出了他的超能粒子炮・改的参数，让你求出其发射的粒子流的威力之和除以\(2333\)所得的余数。

\(\color{#0066ff}{输入格式}\)

第一行一个整数\(t\)表示数据组数。 之后 \(t\) 行，每行两个整数 \(n\)、\(k\)，含义如题面描述。

\(\color{#0066ff}{输出格式}\)

t 行，每行一个整数，表示其粒子流的威力之和模 2333 的值。

\(\color{#0066ff}{输入样例}\)

3
5 5
10 7
1145 14

\(\color{#0066ff}{输出样例}\)

32
968
763

\(\color{#0066ff}{数据范围与提示}\)

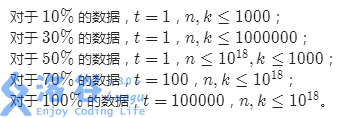
\(\color{#0066ff}{ 题解 }\)

令\(p=2333, f(n,k)=\begin{aligned}\sum_{i=0}^kC_n^i\end{aligned}\)

考虑将\([0,k]\)分成一些段

可以发现，对于\(i\in [0, p*\lfloor\frac k p \rfloor)\)，分成了\(\lfloor\frac k p \rfloor\)段，每段长度为p，根据\((\lfloor\frac i p\rfloor, i \% p)\)可以唯一确定一个i

据Lucas定理，有\(C_n^i=C_{n/p}^{i/p}*C_{n\%p}^{i\%p}\)

根据乘法原理，贡献为\(f(\lfloor\frac n p\rfloor,\lfloor\frac k p\rfloor - 1)*f(n\%p,p-1)\)

考虑剩下的部分，\(i\in[p*\lfloor\frac k p\rfloor,k]\)

显然剩下部分的\(\lfloor \frac i p\rfloor\)是一样的

贡献为\(C_{n/p}^{k/p}*f(n\%p,k\%p)\)

于是，总贡献为\(f(n,k)=C_{n/p}^{k/p}*f(n\%p,k\%p)+f(\lfloor\frac n p\rfloor,\lfloor\frac k p\rfloor - 1)*f(n\%p,p-1)\)

预处理出p以内的f值，在预处理阶乘和逆元之后，\(O(p^2)\)就能处理，这些值调用比较频繁

剩下的C直接Lucas就行了

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int mod = 2333;
const int maxn = 3e3 + 10;
LL f[maxn][maxn], fac[maxn], inv[maxn];
LL ksm(LL x, LL y) {
	LL re = 1LL;
	while(y) {
		if(y & 1) re = re * x % mod;
		x = x * x % mod;
		y >>= 1;
	}
	return re;
}
LL C(LL n, LL m) {
	if(m > n || m < 0) return 0;
	if(n >= mod || m >= mod) return C(n / mod, m / mod) * C(n % mod, m % mod) % mod;
	return ((fac[n] * inv[m] % mod) * inv[n - m]) % mod;
}
LL work(LL n, LL k) {
	if(n < mod && k < mod) return f[n][k];
	return ((C(n / mod, k / mod) * work(n % mod, k % mod) % mod) + (work(n / mod, k / mod - 1) * work(n % mod, mod - 1) % mod)) % mod;
}
void predoit() {
	fac[0] = 1;
	for(int i = 1; i < mod; i++) fac[i] = 1LL * i * fac[i - 1] % mod;
	inv[mod - 1] = ksm(fac[mod - 1], mod - 2);
	for(int i = mod - 2; i >= 0; i--) inv[i] = 1LL * inv[i + 1] * (i + 1) % mod;
	for(int i = 0; i < mod; i++) {
		f[i][0] = 1;
		for(int j = 1; j < mod; j++)
			f[i][j] = (f[i][j - 1] + C(i, j)) % mod;
	}
}
signed main() {
	predoit();
	for(int T = in(); T --> 0;) {
		LL n = in(), k = in();
		printf("%lld\n",  work(n, k));
	}
	return 0;
}