hdu 3718 Different Division

Different Division

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 234    Accepted Submission(s): 90

Problem Description

Now we will give you a graph, there are many points in the graph. We will choose two different points arbitrarily, and connect them as a line. Please tell us that whether these points (Include the two
points referred above) is on the left side of the line, or lying on the line. or on the right side of the line. For example,


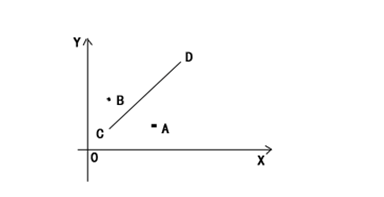
There are four points in the graph: A, B, C, D. we connect C and D. Now C and D form a new line “CD”. Obviously, C and D are lying on the line “CD”. A is on the right side of CD, and B is on the left side of CD. What’s more, A is on the left side of line DC,
and B is on the right side of line DC. So line “CD” and “DC” are different in this problem;

 

Input

The first line of input is a single integer T, indicating the number of test cases. Then exactly T test cases followed. In each case, the first line contains one integer: N, the number of points. Then
N lines followed, each line contains two real numbers X, Y, indicating the coordinates of points. Then one line follows, contains two integers P1 and P2 indicate the P1th point and the P2th point in this case.
1<= T <= 100
2 <= N <= 1000
1<= P1, P2 <= N, P1 != P2
-1000 < X, Y < 1000;

 

Output

For each case, print N lines. According to the order of input, for each point print “Left” if this point is on the left side of line P1P2 , or ”On” if this point is lying on line P1P2 , or ”Right” if this
is on the right side of line P1P2.

 

Sample Input

1
4
1 1
1 2
3 3
2 1
1 3

 

Sample Output

On
Left
On
Right

 

思路：叉积

<span style="font-size:18px;">#include <cstdio>
#include <iostream>
using namespace std;
#define N 1005
double a[N],b[N];

int main()
{
	int t;
	double x1,x2,y1,y2,sum;
	scanf("%d",&t);
	while(t--)
	{
		int n,i;
		scanf("%d",&n);
		for(i = 1; i <= n; i++)
			scanf("%lf%lf",&a[i],&b[i]);
		int p1,p2;
        scanf("%d%d",&p1,&p2);

		 x1 = a[p2] - a[p1];
		 y1 = b[p2] - b[p1];

		for(i=1; i<=n; i++)
		{
			 x2 = a[i] - a[p1];
			 y2 = b[i] - b[p1];

		    sum = x1*y2 - x2*y1;
			if(sum < 0)
				printf("Right\n");
			else if(sum > 0)
				printf("Left\n");
			else printf("On\n");
        }
	}
	return 0;
}</span>