BP神经网络（手写数字识别）

1实验环境

实验环境：CPU i7-3770@3.40GHz，内存8G，windows10 64位操作系统

实现语言：python

实验数据：Mnist数据集

程序使用的数据库是mnist手写数字数据库，数据库有两个版本，一个是别人做好的.mat格式，训练数据有60000条，每条是一个784维的向量，是一张28*28图片按从上到下从左到右向量化后的结果，60000条数据是随机的。测试数据有10000条。另一个版本是图片版的，按0~9把训练集和测试集分为10个文件夹。这里选取.mat格式的数据源。

2 BP（back propagation）神经网络

是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。从结构上讲，BP网络具有输入层、隐藏层和输出层。

3图像转换成数据

图像是由像素组成，每个像素点由红(Red)、绿(Green)、蓝(Blue)三原色组成的，可用RGB表示。例如一个28*28的图片

放大后

图像可以存储成3个28*28的矩阵，第一个表示R的取值（0~255）、第二个表示G的取值（0~255）、第三个表示B的取值（0~255）。

而本例只表示黑白颜色即可，可以将上图转换为1个28*28的矩阵，白~黑由0~255表示，例如颜色越浅数字越小，0表示白，255表示黑。而mnist的mat格式数据源已经将60000条训练集和10000条测试集做了上述处理。

4感知机

感知机接收一些二元变量，然后输出一个二元变量。

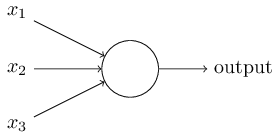
上图的感知机模型有三个输入，一个输出。 怎样计算输出值呢？ Rosenblatt提出了一个简单的算法。他引入了新的实数值变量：。用于表示相对于输出变量每个输入变量的重要性(权重)。

通过变化w和 threshold我们就得到了不同的感知机模型。

5 Sigmoid神经元

对于一个神经网络而言，什么是学习？我们可以认为学习就是给定输入，不断的调整各个权重和偏置，以使得神经网络的输出就是我们想要的结果。这就要求神经网络具有一种性质：改变某一个权重或偏置很小的值，整个神经网络的输出也应该改变很小（数学上，函数连续且可导）。否则这种学习就会非常困难。

不幸的是，感知机组成的神经网络就不具有这种性质。很可能你只是靴微改变某一个权重的值，整个神经网络的输出却会发生质变：原来输出0，现在输出1.

碰到这个问题怎么办呢？前人因此引入了一种新的神经元类型：Sigmoid神经元。

不同于感知机的是，输入变量不仅可以取值0或1，还可以取值0和1之间的任何实数！输出值也不局限于0或1，而是sigmoid函数

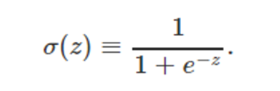
sigmoid神经元其实可以看作感知机的平滑化

6神经网络结构

三层结构，输入层有28*28=784个节点，隐藏层节点数可以变化，输出层有10个节点，表示0~9，若识别数字为1，则输出结果为0100000000，若识别数字为9，则输出结果为0000000001.

下面说明一下各层的表示和各层的关系：（以15个隐藏层节点为例）

输入层：X=(x1,x2,x3…x784)

隐藏层：Y=(y1,y2,y3…y15)

输出层：O=(o1,o2,o3…o10)

两个权重：

输入层到隐藏层的权重：V=(V1,V2,V3…V784)，Vj是一个列向量，表示输入层所有神经元通过Vj加权，得到隐藏层的第j个神经元

隐藏层到输出层的权重：W=(W1,W2,W3…W15)，Wk是一个列向量，表示隐藏层的所有神经元通过Wk加权，得到输出层的第k个神经元

根据我们上面说到的单个神经元的刺激传入和刺激传出，相信到这里很多人应该已经得出下面的各层之间的关系了：

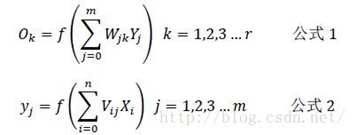
注意：上述公式还要加上偏移量

7误差反向传播算法

如何求得W和V呢，这里要用到一种算法，就是误差反向传播算法(Error Back Propagation Algorithm) ，简称BP 算法。

首先随机地初始化W和V的值，然后代入一些图片进行计算，得到一个输出，当然由于W和V参数不会刚好很完美，输出自然不会是像上文说的，刚好就是{1 0 0 0 0 0 0 0 0 0}这一类，例如{0.7 0 0 0.1 0.2 0 0 0 0 0.1}.所以存在误差，根据这个误差就可以反过来修正W和V的值，修正后的W和V可以使输出更加的靠近于理想的输出，这就是所谓的“误差反向传播”的意思，修正一次之后，再代入其他一些图片，输出离理想输出又靠近了一点，我们又继续计算误差，然后修正W和V的值，就这样经过很多次的迭代计算，最终多次修正得到了比较完美的W和V矩阵，它可以使得输出非常靠近于理想的输出，至此我们的工作完成度才是100%了。

逆向传播算法的数学推导.....(No figures are omitted below)

推导结果：

d表示正确标签，o表示训练输出，y表示隐藏层的值。另外为了使权值调整更加灵活加入一个放缩倍数η（权值学习率）使得，

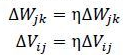
改变η的大小即可改变每一次调节的幅度，η大的话调节更快，小则调节慢，但是过大容易导致振荡。

8手写体数字识别算法实现步骤

1)      读入训练数据：训练样本、训练样本标签

2)      神经网络配置：参数的初始化（各层节点数、各层权值学习率、各层偏移量等）

3)      激活函数实现：sigmoid函数

4)      训练：60000个数据量的训练集；前向过程，后向过程（反馈调整各层权重和偏移量）

5)      测试：10000个数据量的测试集，获取正确率

9程序结果分析

主要参数：

输入层节点数，隐藏层节点数，输出层节点数，输入层权矩阵，隐藏层权矩阵，输入层偏置向量，隐藏层偏置向量，输入层权值学习率，隐藏层学权值习率

不可变参数：

输入层节点数（784），输出层节点数（10）

随机参数（随机数生成）：

输入层权矩阵，隐藏层权矩阵，输入层偏置向量，隐藏层偏置向量

可控参数：

隐藏层节点数，输入层权值学习率，隐藏层学权值习率

隐藏层节点数对算法的影响：

参数表1

隐藏层节点数	10
输入层权值学习率	0.3
隐藏层学权值习率	0.3

结果1（20s）

	0	1	2	3	4	5	6	7	8	9
测试集	980	1135	1032	1010	982	892	958	1028	974	1009
正确数	946	1111	860	906	915	754	887	896	800	903
正确率	96.5%	97.9%	83.3%	89.7%	93.2%	84.5%	92.6%	87.2%	82.1%	89.5%
总	89.78%

参数表2

隐藏层节点数	15
输入层权值学习率	0.3
隐藏层学权值习率	0.3

结果2（27s）

	0	1	2	3	4	5	6	7	8	9
测试集	980	1135	1032	1010	982	892	958	1028	974	1009
正确数	948	1117	873	909	872	751	929	898	867	950
正确率	96.7%	98.4%	84.6%	90.0%	88.8%	84.2%	97.0%	87.4%	89.0%	94.2%
总	91.14%

参数表3

隐藏层节点数	30
输入层权值学习率	0.3
隐藏层学权值习率	0.3

结果3（46s）

	0	1	2	3	4	5	6	7	8	9
测试集	980	1135	1032	1010	982	892	958	1028	974	1009
正确数	953	1124	913	963	931	796	919	919	892	952
正确率	97.2%	99.0%	88.5%	95.3%	94.8%	89.2%	95.9%	89.4%	91.6%	94.4%
总	93.62%

当隐藏层节点数增到100时，算法跑了137s，总正确率为94.94%

算法正确率收敛于95%……算法遇到了瓶颈......

权值学习率对算法的影响：

 

输入节点784，隐藏层节点10，输出层节点10

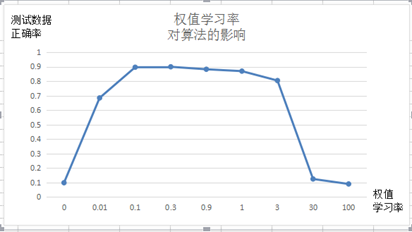
令输入层和隐藏层权值学习率共用一个参数的条件下，权值学习率n取值范围为[0.1,1]算法正确率最高。

算法手写体数字识别

正确率较高的数字是1、0

正确率较低的数字是2、5

谢 谢！     未 完 待 续 ...