Bezier贝塞尔曲线的原理、二次贝塞尔曲线的实现

Bezier曲线的原理

Bezier曲线是应用于二维图形的曲线。曲线由顶点和控制点组成，通过改变控制点坐标可以改变曲线的形状。

一次Bezier曲线公式：

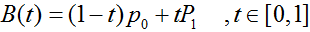
一次Bezier曲线是由P0至P1的连续点，描述的一条线段

二次Bezier曲线公式：

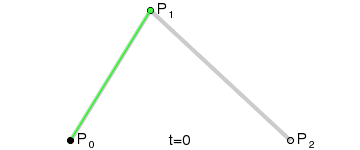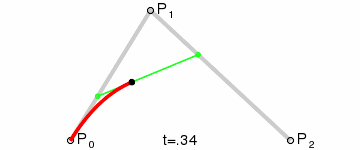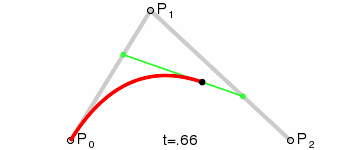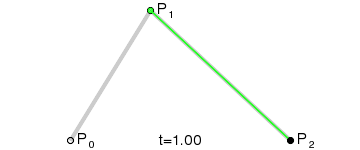
二次Bezier曲线是 P0至P1 的连续点Q0和P1至P2 的连续点Q1 组成的线段上的连续点B(t)，描述一条抛物线。

三次Bezier曲线公式：

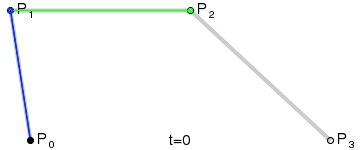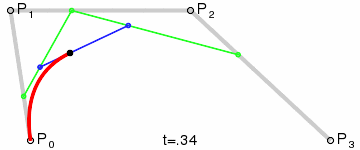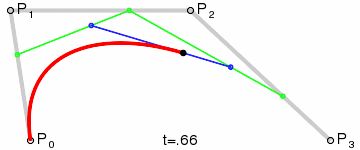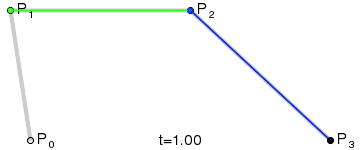
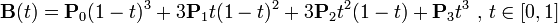
二次Bezier曲线的实现

#include <vector>

class CBezierCurve
{
public:
    CBezierCurve();
    ~CBezierCurve();

    void SetCtrlPoint(POINT& stPt);

    bool CreateCurve();

    void Draw(CDC* pDC);

private:
        // 主要算法，计算曲线各个点坐标
    void CalCurvePoint(float t, POINT& stPt);

private:
        // 顶点和控制点数组
    std::vector<POINT> m_vecCtrlPt;
        // 曲线上各点坐标数组
    std::vector<POINT> m_vecCurvePt;
};

    #include <math.h>
    #include "BezierCurve.h"  

    CBezierCurve::CBezierCurve()
    {
    }  

    CBezierCurve::~CBezierCurve()
    {
    }  

    void CBezierCurve::SetCtrlPoint(POINT& stPt)
    {
        m_vecCtrlPt.push_back(stPt);
    }  

    void CBezierCurve::CreateCurve()
    {
        // 确保是二次曲线，2个顶点一个控制点
        assert(m_vecCtrlPt.size() == );  

        // t的增量， 可以通过setp大小确定需要保存的曲线上点的个数
        float step = 0.01;
        for (float t = 0.0; t <= 1.0; t += step)
        {
            POINT stPt;
            CalCurvePoint(t, stPt);
            m_vecCurvePt.push_back(stPt);
        }
    }  

    void CBezierCurve::Draw(CDC* pDC)
    {
        // 画出曲线上个点，若不连续可以用直线连接各点
        int nCount = m_vecCurvePt.size();
        for (int i = ; i < nCount; ++i)
        {
            pDC->SetPixel(m_vecCurvePt[i], 0x000000);
        }
    }  

    void CBezierCurve::CalCurvePoint(float t, POINT& stPt)
    {
            // 确保是二次曲线，2个顶点一个控制点
        assert(m_vecCtrlPt.size() == );  

        // 计算曲线点坐标，此为2次算法，改变此处可以实现多次曲线
        float x = (float)m_vecCtrlPt[].x * pow( - t, )   +
                  (float)m_vecCtrlPt[].x * t * ( - t) *  +
                  (float)m_vecCtrlPt[].x * pow(t, );
        float y = (float)m_vecCtrlPt[].y * pow( - t, )   +
                  (float)m_vecCtrlPt[].y * t * ( - t) *  +
                  (float)m_vecCtrlPt[].y * pow(t, );
        stPt.x =x;
        stPt.y= y;
    }