Normal Equation

一、Normal Equation

　我们知道梯度下降在求解最优参数\(\theta\)过程中需要合适的\(\alpha\)，并且需要进行多次迭代，那么有没有经过简单的数学计算就得到参数\(\theta\)呢？

　下面我们看看Ng 4-6 中的房价预测例子：

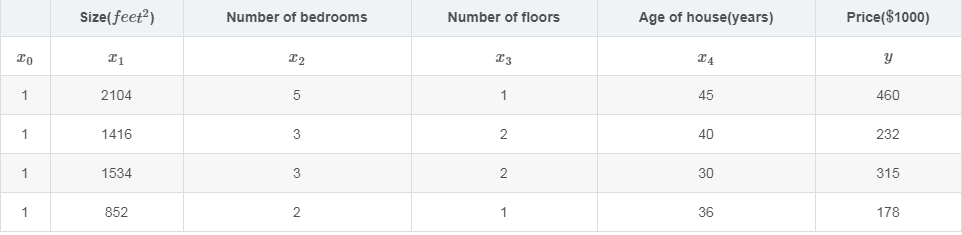
　其中\( m = 4, n = 4 \)。在机器学习中，线性回归一般都增加额外的一列特征\(x_0 = 1\)，其中我们特征矩阵\(X\)和值向量\(y\)分别为：

\begin{bmatrix}1 & 2104 & 5 & 1 & 45 \\ 1 & 1416 & 3 & 2 & 40 \\ 1 & 1534 & 3 & 2 & 30 \\ 1 & 852 & 2 & 1 & 36 \end{bmatrix}

\begin{bmatrix}460\\ 232\\ 315\\178\end{bmatrix}

　而我们的参数\(\theta\)为：

\begin{bmatrix}\theta_0\\ \theta_1\\ \theta_2\\ ...\\\theta_n\end{bmatrix}

　那最终的参数\(\theta\)应该为：

\(\theta = (X^TX)^{-1}X^Ty\)

二、证明

　我们知道单位矩阵\(E\)有一个性质：

\( A \times A^{-1} = A^{-1} \times A = E \)

 　首先：

\( y = X \cdot \theta \)

　左右同时乘\(X^T\)：

\(X^Ty = X^TX \cdot \theta\)

　左右再同时乘\(X^TX^{-1}\)：

\((X^TX)^{-1}X^Ty = (X^TX)^{-1}X^TX \cdot \theta\)

　而我们已知矩阵的逆乘以矩阵得到单位矩阵\(E\)：

\((X^TX)^{-1}X^Ty = \theta\)

三、和梯度下降作比较

　Normal Equation有一个好处：不需要进行Feature scaling，而Feature scaling对于梯度下降是必须的

　如何来选择使用哪种方法么呢？一般如果特征维度不超过1000的话，Normal Equation还是可选的。

　此外，如果\((X^TX)^{-1}\)不可逆怎么办？

　　1）确保不存在冗余特征，比如

　　因为\(1m = 3.28feet\)，所以\(x_1 = (3.28)^2 * x_2\)，我们知道线性代数中出现这种线性相关的情况，其行列式值为0，所以不可逆，我们只需确保不会出现冗余特征即可。

　　2）特征数量\(n\)过多，而样本数量\(m\)过少：解决方法为删除一部分特征，或者增加样本数量。

四、说明

　此文参考：https://blog.csdn.net/artprog/article/details/51172025