JavaScript 浮点数运算的精度问题

问题描述

在 JavaScript 中整数和浮点数都属于 Number 数据类型，所有数字都是以 64 位浮点数形式储存，即便整数也是如此。 所以我们在打印 1.00 这样的浮点数的结果是 1 而非 1.00 。在一些特殊的数值表示中，例如金额，这样看上去有点变扭，但是至少值是正确了。然而要命的是，当浮点数做数学运算的时候，你经常会发现一些问题，举几个例子：

JavaScript 代码:

// 加法 =====================

// 0.1 + 0.2 = 0.30000000000000004

// 0.7 + 0.1 = 0.7999999999999999

// 0.2 + 0.4 = 0.6000000000000001

// 2.22 + 0.1 = 2.3200000000000003

// 减法 =====================

// 1.5 - 1.2 = 0.30000000000000004

// 0.3 - 0.2 = 0.09999999999999998

// 乘法 =====================

// 19.9 * 100 = 1989.9999999999998

// 19.9 * 10 * 10 = 1990

// 1306377.64 * 100 = 130637763.99999999

// 1306377.64 * 10 * 10 = 130637763.99999999

// 0.7 * 180 = 125.99999999999999

// 9.7 * 100 = 969.9999999999999

// 39.7 * 100 = 3970.0000000000005

// 除法 =====================

// 0.3 / 0.1 = 2.9999999999999996

// 0.69 / 10 = 0.06899999999999999

问题的原因

似乎是不可思议。小学生都会算的题目，JavaScript 不会？我们来看看其真正的原因。

JavaScript 里的数字是采用 IEEE 754 标准的 64 位双精度浮点数。该规范定义了浮点数的格式，对于64位的浮点数在内存中的表示，最高的1位是符号位，接着的11位是指数，剩下的52位为有效数字，具体：

第0位：符号位， s 表示 ，0表示正数，1表示负数；

第1位到第11位：储存指数部分， e 表示 ；

第12位到第63位：储存小数部分（即有效数字），f 表示，

如图：

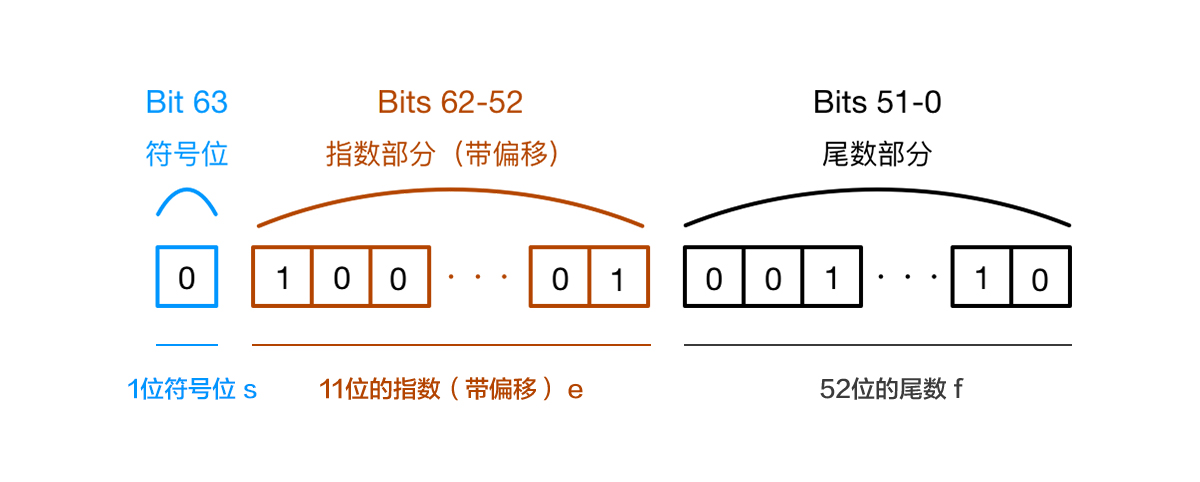
符号位决定了一个数的正负，指数部分决定了数值的大小，小数部分决定了数值的精度。 IEEE 754规定，有效数字第一位默认总是1，不保存在64位浮点数之中。也就是说，有效数字总是1.xx…xx的形式，其中xx..xx的部分保存在64位浮点数之中，最长可能为52位。因此，JavaScript提供的有效数字最长为53个二进制位（64位浮点的后52位+有效数字第一位的1）。

计算过程

比如在 JavaScript 中计算 0.1 + 0.2时，到底发生了什么呢？

首先，十进制的0.1和0.2都会被转换成二进制，但由于浮点数用二进制表达时是无穷的，例如。

JavaScript 代码:

0.1 -> 0.0001100110011001...(无限)

0.2 -> 0.0011001100110011...(无限)

IEEE 754 标准的 64 位双精度浮点数的小数部分最多支持 53 位二进制位，所以两者相加之后得到二进制为：

JavaScript 代码:

0.0100110011001100110011001100110011001100110011001100

因浮点数小数位的限制而截断的二进制数字，再转换为十进制，就成了 0.30000000000000004。所以在进行算术计算时会产生误差。

整数的精度问题

在 Javascript 中，整数精度同样存在问题，先来看看问题：

JavaScript 代码:

console.log(19571992547450991); //=> 19571992547450990

console.log(19571992547450991===19571992547450992); //=> true

同样的原因，在 JavaScript 中 Number类型统一按浮点数处理，整数是按最大54位来算最大(253

- 1，Number.MAX_SAFE_INTEGER,9007199254740991) 和最小(-(253

- 1)，Number.MIN_SAFE_INTEGER,-9007199254740991) 安全整数范围的。所以只要超过这个范围，就会存在被舍去的精度问题。

当然这个问题并不只是在 Javascript 中才会出现，几乎所有的编程语言都采用了 IEEE-745 浮点数表示法，任何使用二进制浮点数的编程语言都会有这个问题，只不过在很多其他语言中已经封装好了方法来避免精度的问题，而 JavaScript 是一门弱类型的语言，从设计思想上就没有对浮点数有个严格的数据类型，所以精度误差的问题就显得格外突出。

解决方案

方案一：如果有精度要求，可以用toFixed方法处理

var num1 = 0.1;

var num2 = 0.2;

alert( parseFloat((num1 + num2).toFixed(2)) === 0.30 );

方案二：通用处理方案：把需要计算的数字乘以 10 的 n 次幂，换算成计算机能够精确识别的整数，然后再除以 10 的 n 次幂

复制代码

formatNum = function(f, digit) {

var m = Math.pow(10, digit);

return parseInt(f * m, 10) / m;

}

var num1 = 0.1;

var num2 = 0.2;

alert(Math.formatFloat(num1 + num2, 1) === 0.3)

方案三

还有一些其他的解决方案，简单的说需要将浮点数转换字符串，分隔成为整数部分和小数部分，小数部分再转换为整数，计算结果后，再转换为浮点数。这过程有点复杂.

加法函数

JavaScript 代码:

/**

** 加法函数，用来得到精确的加法结果

** 说明：javascript的加法结果会有误差，在两个浮点数相加的时候会比较明显。这个函数返回较为精确的加法结果。

** 调用：accAdd(arg1,arg2)

** 返回值：arg1加上arg2的精确结果

**/

function accAdd(arg1, arg2) {

var r1, r2, m, c;

try {

r1 = arg1.toString().split(".")[1].length;

}

catch (e) {

r1 = 0;

}

try {

r2 = arg2.toString().split(".")[1].length;

}

catch (e) {

r2 = 0;

}

c = Math.abs(r1 - r2);

m = Math.pow(10, Math.max(r1, r2));

if (c > 0) {

var cm = Math.pow(10, c);

if (r1 > r2) {

arg1 = Number(arg1.toString().replace(".", ""));

arg2 = Number(arg2.toString().replace(".", "")) * cm;

} else {

arg1 = Number(arg1.toString().replace(".", "")) * cm;

arg2 = Number(arg2.toString().replace(".", ""));

}

} else {

arg1 = Number(arg1.toString().replace(".", ""));

arg2 = Number(arg2.toString().replace(".", ""));

}

return (arg1 + arg2) / m;

}

//给Number类型增加一个add方法，调用起来更加方便。

Number.prototype.add = function (arg) {

return accAdd(arg, this);

};

减法函数

JavaScript 代码:

/**

** 减法函数，用来得到精确的减法结果

** 说明：javascript的减法结果会有误差，在两个浮点数相减的时候会比较明显。这个函数返回较为精确的减法结果。

** 调用：accSub(arg1,arg2)

** 返回值：arg1加上arg2的精确结果

**/

function accSub(arg1, arg2) {

var r1, r2, m, n;

try {

r1 = arg1.toString().split(".")[1].length;

}

catch (e) {

r1 = 0;

}

try {

r2 = arg2.toString().split(".")[1].length;

}

catch (e) {

r2 = 0;

}

m = Math.pow(10, Math.max(r1, r2)); //last modify by deeka //动态控制精度长度

n = (r1 >= r2) ? r1 : r2;

return ((arg1 * m - arg2 * m) / m).toFixed(n);

}

// 给Number类型增加一个mul方法，调用起来更加方便。

Number.prototype.sub = function (arg) {

return accMul(arg, this);

};

乘法函数

JavaScript 代码:

/**

** 乘法函数，用来得到精确的乘法结果

** 说明：javascript的乘法结果会有误差，在两个浮点数相乘的时候会比较明显。这个函数返回较为精确的乘法结果。

** 调用：accMul(arg1,arg2)

** 返回值：arg1乘以 arg2的精确结果

**/

function accMul(arg1, arg2) {

var m = 0, s1 = arg1.toString(), s2 = arg2.toString();

try {

m += s1.split(".")[1].length;

}

catch (e) {

}

try {

m += s2.split(".")[1].length;

}

catch (e) {

}

return Number(s1.replace(".", "")) * Number(s2.replace(".", "")) / Math.pow(10, m);

}

// 给Number类型增加一个mul方法，调用起来更加方便。

Number.prototype.mul = function (arg) {

return accMul(arg, this);

};

除法函数

JavaScript 代码:

/**

** 除法函数，用来得到精确的除法结果

** 说明：javascript的除法结果会有误差，在两个浮点数相除的时候会比较明显。这个函数返回较为精确的除法结果。

** 调用：accDiv(arg1,arg2)

** 返回值：arg1除以arg2的精确结果

**/

function accDiv(arg1, arg2) {

var t1 = 0, t2 = 0, r1, r2;

try {

t1 = arg1.toString().split(".")[1].length;

}

catch (e) {

}

try {

t2 = arg2.toString().split(".")[1].length;

}

catch (e) {

}

with (Math) {

r1 = Number(arg1.toString().replace(".", ""));

r2 = Number(arg2.toString().replace(".", ""));

return (r1 / r2) * pow(10, t2 - t1);

}

}

//给Number类型增加一个div方法，调用起来更加方便。

Number.prototype.div = function (arg) {

return accDiv(this, arg);

};