[matlab] 10.最小覆盖

clear all;
close all;
clc;

n=100;
p=rand(n,2);

p1=p(1,:); %取第一行的值 P1点
p2=p(2,:); %取第二行的值 P2点
r=sqrt((p1(1)-p2(1))^2+(p1(2)-p2(2))^2)/2; %求两点半径
cenp=(p1+p2)/2;   %求两点中点

for i=3:n
    newp=p(i,:);    %从第三行开始 储存新的点
    d=sqrt((cenp(1)-newp(1))^2+(cenp(2)-newp(2))^2);  %圆心到新的点的距离为d
    if d>r %当距离大于现有半径的时候,赋值更大的半径
        r=(r+d)/2;
        cenp=cenp+(d-r)/d*(newp-cenp); %按比例位移中心
    end
end

hold on;
plot(p(:,1),p(:,2),'rs');
x0=cenp(1); %圆心横坐标
y0=cenp(2);
theta=0:0.01:2*pi;
x=x0+r*cos(theta);
y=y0+r*sin(theta);
plot(x,y,'k-',x0,y0,'k.');
axis equal

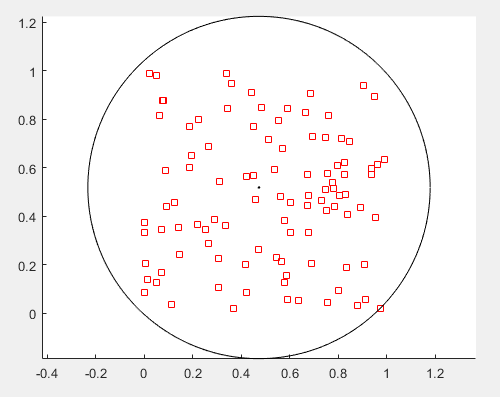
最小覆盖圆

最小覆盖矩形可能是倾斜的。

求法如下：

1.求多边形凸包，这里凸包直接调用系统函数了。

2.将凸包两个相邻的点连线作为矩形一条边。

3.寻找凸包上距离已得到的边最远的点，过该点做平行线，得到矩形第二条边。

4.将凸包上点向已求得的边投影，求得投影点相距最远的两个点，过该两点做直线，作为矩形另外两条边。

5.遍历凸包所有相邻两点从新运行2~4，将面积最小的矩形作为求得结果。

通常情况下，矩形会过随机点中的5个点。

clear all;close all;clc;

n=30;
p=rand(n,2);

ind=convhull(p(:,1),p(:,2));
l=length(ind);

hull=p(ind,:);          %随机点凸包

area=inf;
for i=2:l
    p1=hull(i-1,:);     %凸包上两个点
    p2=hull(i,:);

    k1=(p1(2)-p2(2))/(p1(1)-p2(1));     %连接两点的直线，作为矩形的一条边
    b1=p1(2)-k1*p1(1);

    d=abs(hull(:,1)*k1-hull(:,2)+b1)/sqrt(k1^2+1);  %所有凸包上的点到k1,b1直线的距离

    [h ind]=max(d);                     %得到距离最大的点距离，即为高，同时得到该点坐标
    b2=hull(ind,2)-k1*hull(ind,1);      %相对k1,b1直线相对的另一条平行边k1,b2;

    k2=-1/k1;                           %以求得的直线的垂线斜率

    b=hull(:,2)-k2*hull(:,1);           %过凸包所有点构成的k2,b直线系
    x1=-(b1-b)/(k1-k2);                 %凸包上所有点在已求得的第一条边的投影
    y1=-(-b*k1+b1*k2)/(k1-k2);

    x2=-(b2-b)/(k1-k2);                 %凸包上所有点在已求得的第二条边的投影
    y2=-(-b*k1+b2*k2)/(k1-k2);

    [junk indmax1]=max(x1);             %投影在第一条边上x方向最大与最小值
    [junk indmin1]=min(x1);

    [junk indmax2]=max(x2);             %投影在第二条边上x方向最大与最小值
    [junk indmin2]=min(x2);

    w=sqrt((x1(indmax1)-x1(indmin1))^2+(y1(indmax1)-y1(indmin1))^2);    %矩形的宽

    if area>=h*w                        %使面积最小
        area=h*w;
        pbar=[x1(indmax1) y1(indmax1);  %矩形四个角点
              x2(indmax2) y2(indmax2);
              x2(indmin2) y2(indmin2);
              x1(indmin1) y1(indmin1)];
    end
end
pbar(5,:)=pbar(1,:);

hold on;
plot(p(:,1),p(:,2),'.');
plot(pbar(:,1),pbar(:,2),'r')
axis equal;

最小覆盖矩形