c/c++ 有向无环图 directed acycline graph

c/c++ 有向无环图 directed acycline graph

概念：

图中点与点之间的线是有方向的，图中不存在环。用邻接表的方式，实现的图。

名词：

• 顶点的入度：到这个顶点的线的数量。
• 顶点的出度：从这个顶点出发的线的数量。

实现思路：

1，计算出每个顶点的入度，存放到辅助数组cnt中

2，找到入度为0的顶点集合。

3，从入度为0的顶点集合，拿出一个顶点，这个顶点就是第一个顶点（不唯一）。

4，找到与以3处顶点为出发点的顶点，然后把这些顶点的入度减一，减一后发现如果入度为0了，更新辅助数组cnt

5，重复2-4

难点：

辅助数组cnt的作用：

• 刚开始是存放每个顶点的入度
• 找到入度为0的顶点后，入栈；出栈的元素就是找到的顶点，发现入度为0的顶点后，继续入栈，然后出栈...

辅助数组cnt的运用，建议用gdb，多debug几次，就能明白了。

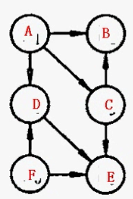
图为下图1：

图1

graph_link.h

#ifndef __graph_link__
#define __graph_link__

#include <stdio.h>
#include <malloc.h>
#include <assert.h>
#include <memory.h>

#define default_vertex_size 10
#define T char

//边的结构
typedef struct Edge{
  //顶点的下标
  int idx;
  //指向下一个边的指针
  struct Edge* link;
}Edge;

//顶点的结构
typedef struct Vertex{
  //顶点的值
  T data;
  //边
  Edge* adj;
}Vertex;

//图的结构
typedef struct GraphLink{
  int MaxVertices;
  int NumVertices;
  int NumEdges;

  Vertex* nodeTable;
}GraphLink;

//初始化图
void init_graph_link(GraphLink* g);
//显示图
void show_graph_link(GraphLink* g);
//插入顶点
void insert_vertex(GraphLink* g, T v);
//插入边尾插
void insert_edge_tail(GraphLink* g, T v1, T v2);
//插入边头插
void insert_edge_head(GraphLink* g, T v1, T v2);
//取得指定顶点的第一个后序顶点
int get_first_neighbor(GraphLink* g, T v);
//取得指定顶点v1的临街顶点v2的第一个后序顶点
int get_next_neighbor(GraphLink* g, T v1, T v2);

//拓扑排序
void topo_sort(GraphLink* g);

#endif

graph_link.c

#include "graph_link.h"

//初始化图
void init_graph_link(GraphLink* g){
  g->MaxVertices = default_vertex_size;
  g->NumVertices = g->NumEdges = 0;

  g->nodeTable = (Vertex*)malloc(sizeof(Vertex) * g->MaxVertices);
  assert(NULL != g->nodeTable);
  for(int i = 0; i < g->MaxVertices; ++i){
    g->nodeTable[i].adj = NULL;
  }
}

//显示图
void show_graph_link(GraphLink* g){
  if(NULL == g)return;
  for(int i = 0; i < g->NumVertices; ++i){
    printf("%d %c->", i, g->nodeTable[i].data);
    Edge* p = g->nodeTable[i].adj;
    while(NULL != p){
      printf("%d->", p->idx);
      p = p->link;
    }
    printf(" NULL\n");
  }
}

//插入顶点
void insert_vertex(GraphLink* g, T v){
  if(g->NumVertices >= g->MaxVertices)return;
  g->nodeTable[g->NumVertices++].data = v;
}

//查找顶点的index
int getVertexIndex(GraphLink* g, T v){
  for(int i = 0; i < g->NumVertices; ++i){
    if(v == g->nodeTable[i].data)return i;
  }
  return -1;
}

//创建边
void buyEdge(Edge** e, int idx){
  Edge* p = (Edge*)malloc(sizeof(Edge));
  p->idx = idx;
  p->link = NULL;
  if(NULL == *e){
    *e = p;
  }
  else{
    Edge* tmp = *e;
    while(tmp->link != NULL){
      tmp = tmp->link;
    }
    tmp->link = p;
  }
}
//插入边(尾插）
void insert_edge_tail(GraphLink* g, T v1, T v2){
  int p1 = getVertexIndex(g, v1);
  int p2 = getVertexIndex(g, v2);

  if(p1 == -1 || p2 == -1)return;

  buyEdge(&(g->nodeTable[p1].adj), p2);
  g->NumEdges++;
  buyEdge(&(g->nodeTable[p2].adj), p1);
  g->NumEdges++;

}
//插入边(头插）
void insert_edge_head(GraphLink* g, T v1, T v2){
  int p1 = getVertexIndex(g, v1);
  int p2 = getVertexIndex(g, v2);

  if(p1 == -1 || p2 == -1)return;

  Edge* p = (Edge*)malloc(sizeof(Edge));
  p->idx = p2;
  p->link = g->nodeTable[p1].adj;
  g->nodeTable[p1].adj = p;

  /*
  p = (Edge*)malloc(sizeof(Edge));
  p->idx = p1;
  p->link = g->nodeTable[p2].adj;
  g->nodeTable[p2].adj = p;
  */
}

//取得指定顶点的第一个后序顶点
int get_first_neighbor(GraphLink* g, T v){
  int i = getVertexIndex(g, v);
  if (-1 == i)return -1;
  Edge* p = g->nodeTable[i].adj;
  if(NULL != p)
    return p->idx;
  else
    return -1;
}

//取得指定顶点v1的临街顶点v2的第一个后序顶点
int get_next_neighbor(GraphLink* g, T ve1, T ve2){
  int v1 = getVertexIndex(g, ve1);
  int v2 = getVertexIndex(g, ve2);
  if(v1 == -1 || v2 == -1)return -1;

  Edge* t = g->nodeTable[v1].adj;
  while(t != NULL && t->idx != v2){
    t = t->link;
  }
  if(NULL != t && t->link != NULL){
    return t->link->idx;
  }
  return -1;
}

//拓扑排序
void topo_sort(GraphLink* g){
  int n = g->NumVertices;

  //表示各个顶点的入度，先都初始化为0
  int* cnt = (int*)malloc(sizeof(int) * n);
  assert(NULL != cnt);
  for(int i = 0; i < n; ++i){
    cnt[i] = 0;
  }

  Edge* p;
  //算出各个顶点的入度
  for(int i = 0; i < n; ++i){
    p = g->nodeTable[i].adj;
    while(p != NULL){
      cnt[p->idx]++;
      p = p->link;
    }
  }

  int top = -1;
  for(int i = 0; i < n; ++i){
    if(cnt[i] == 0){
      //入度为0的顶点入栈（模拟入栈）
      cnt[i] = top; //push
      top = i;
    }
  }

  int v,w;
  for(int i = 0; i < n; ++i){
    if(top == -1)return;//有回路存在

    v = top;         //模拟出栈
    top = cnt[top];
    printf("%c->", g->nodeTable[v].data);
    w = get_first_neighbor(g, g->nodeTable[v].data);
    while(-1 != w){
      if(--cnt[w] == 0){
        //入度为0的顶点入栈（模拟入栈）
	cnt[w] = top;
	top = w;
      }
      w = get_next_neighbor(g,g->nodeTable[v].data,g->nodeTable[w].data);
    }
  }
  free(cnt);
}

graph_linkmain.c

#include "graph_link.h"

int main(){
  GraphLink gl;
  //初始化图
  init_graph_link(&gl);
  //插入节点
  insert_vertex(&gl, 'A');
  insert_vertex(&gl, 'B');
  insert_vertex(&gl, 'C');
  insert_vertex(&gl, 'D');
  insert_vertex(&gl, 'E');
  insert_vertex(&gl, 'F');

  //插入边(头插)
  insert_edge_head(&gl, 'A', 'B');
  insert_edge_head(&gl, 'A', 'C');
  insert_edge_head(&gl, 'A', 'D');
  insert_edge_head(&gl, 'C', 'B');
  insert_edge_head(&gl, 'C', 'E');
  insert_edge_head(&gl, 'D', 'E');
  insert_edge_head(&gl, 'F', 'D');
  insert_edge_head(&gl, 'F', 'E');

  //显示图
  show_graph_link(&gl);

  //拓扑排序
  topo_sort(&gl);

  printf("\n");
}

完整代码

编译方法：gcc -g graph_link.c graph_linkmain.c