贝叶斯定理推导（Bayes' Theorem Induction）

这里用Venn diagram来不严谨地推导一下贝叶斯定理。

假设A和B为两个不相互独立的事件。

交集（intersection）：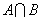 

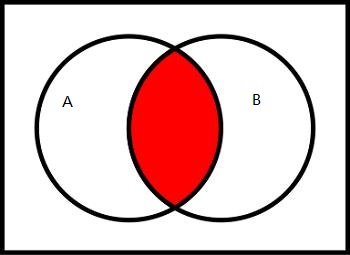
上图红色部分即为事件A和事件B的交集。

并集（union）：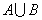 

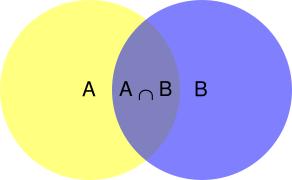
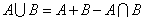
由Venn diagram可以看出，在事件B已经发生的情况下，事件A发生的概率为事件A和事件B的交集除以事件B：

同理，在事件A已经发生的情况下，事件B发生的概率为事件A和事件B的交集除以事件A：

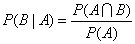
注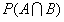：表示 A，B 事件同时发生的概率，如果 A 和 B 是相互独立的两个事件，那么：。

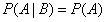由上面的公式可以得到：

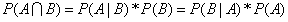
然后，我们就可以得到贝叶斯定理：

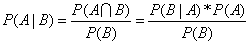
其中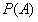： 是先验概率（prior probability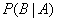），是条件概率（conditional probability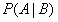），是后验概率（posterior probability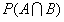）。是联合概率（joint probability），通常写成P(A,B)。

注：条件概率 P(B|A) ---> 给定事件A，事件B发生的概率（probability of event B occuring given event A）。

又根据Law of Total Probability：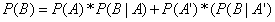 

注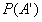：表示事件A不发生的概率。

这个可以用probability tree来帮助理解一下：

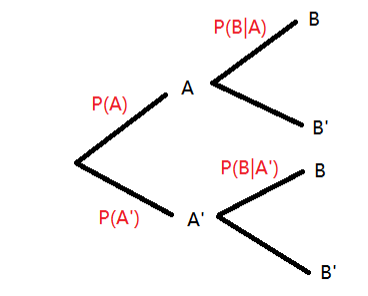
因此，贝叶斯定理可以扩展为：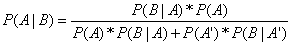 

贝叶斯定理通常用于由已知的先验概率和条件概率，推算出后验概率。

举一个简单的例子：某地平时下雨的概率是0.3，小明平时带伞的概率是0.4，小明下雨天带伞的概率是0.8。某一天小明带了伞，请问这天下雨的概率是多少？

解答：也就是需要求P(下雨|小明带伞)，把上面的数字代入公式即：

这个例子的先验概率是平时下雨的概率0.3，由于我们已知小明带了伞这一信息，因此我们可以估算出后验概率，也就是当天下雨的概率是0.6。

先验概率是怎么得来的呢？通常是人们的经验总结或者说是估算，比如说某地一个月里面下了3天雨，我们就估算某地平时下雨的概率是0.3。

如果条件不止一个呢？让我们把上面的例子改一下：某地平时下雨的概率是0.3，平时刮风的概率是0.4，下雨天刮风的概率是0.6，小明平时带伞的概率是0.4，小明下雨天带伞的概率是0.8。某一天小明带了伞，且当天在刮风，请问这天下雨的概率是多少？

解答：也就是需要求P(下雨|小明带伞，刮风)，把上面的数字代入公式即：

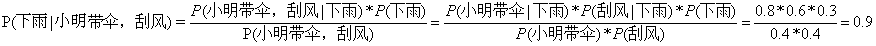
注：这里假设小明带伞和刮风之间没有关联，两条件互不影响（条件独立假设），因此属于朴素贝叶斯的范畴。

长久以来，人们信奉的是频率主义。比如把一枚硬币抛10000次，有5000次正面朝上，5000次反面朝上，那么我们就可以得知抛这枚硬币，其正面朝上的概率是0.5。通常，我们需要某一事件发生足够多的次数，我们才可以观察到它的规律。

在现实生活中，很多事件并不会在相对较短的时间内多次发生。这时候，贝叶斯定理就发挥作用了。比如说我们想知道刮风天下雨的概率是多少，我们不用等10000个刮风天，看其中有几天下了雨。我们只需要估算出下雨天会刮风的概率，平时下雨的概率，平时刮风的概率，就可以估算出刮风天会下雨的概率是多少了。先验概率估算得不准确并没有关系，人们可以通过未来事件的发生情况，不断对后验概率做出调整。