LCA的几种做法

P3379 LCA

---

$ 1:$蜗牛爬式

void dfs(int u,int fa) {
    f[u]=fa;//预处理father
    for(int i=head[u]; i; i=e[i].nxt) if(e[i].v!=fa) {
            int &w=e[i].w,&v=e[i].v;
            dis[v]=dis[u]+w;
            h[v]=h[u]+1;//预处理深度
            dfs(v,u);
        }
}
int LCA(int x,int y) {
    while(h[x]<h[y])y=f[y];
    while(h[x]>h[y])x=f[x];//移动至同一深度
    while(x!=y) x=f[x],y=f[y];
    return x;
}

复杂度:\(O( log(n) )\) ~ \(O(n)\)

当然,这东西非常好卡，一卡就凉\(->\) \(O(n)\)

事实上，这种暴力算法，数据达到5e5时绝对会T(不卡你也会)...

\(2:\) 倍增大法

复杂度 预处理:\(O(nlog(n))\) 查询:\(O(log(n))\),有常数

算法核心:

\(1.\) 预处理\(fa[i][k]\):i上的第\(2^k\)个祖先(如果没有,记为\(-1\))

--- 预处理方法 \(O(n log(log(n)))\)

--- 递推式 \(fa[i][k]=fa[fa[i][k-1][k-1]\)

--- 外层接k的循环,内层接i的循环

void dfs(int u,int f) {
    fa[u][0]=f;
    for(reg int i=head[u]; i; i=nxt[i]) if(to[i]!=f) {
            reg int &v=to[i],&w=x[i];
            h[v]=h[u]+1;
            dis[v]=dis[u]+w;
            dfs(v,u);
        }
}
void LCA_init() {
    dfs(1,-1);
    for(reg int j=0; j+1<L; j++)
        for(reg int i=1; i<=n; i++) {
            if(fa[i][j]<0)fa[i][j+1]=-1;
            else fa[i][j+1]=fa[f[i][j]][j];
        }
}

\(2.\)通过一种类似于二进制枚举的方法找爸爸,其原理与蜗牛爬式类似

--- \(step1:\)将x,y移动到同一深度

--- \(step2:\)枚举x,y的上层祖先,防止过度移动,倒着循环

int LCA(int x,int y) {
    if(h[x]>h[y])swap(x,y);
    int del=h[y]-h[x];
    for(int i=0; (1<<i)<=del; i++)
        if(del&(1<<i))
            y=f[y][i];
    if(x==y)return x;//这句话很关键,很容易忘,不加会过度
    for(int i=ceil(log(h[x])); i>=0; i--)
        if(fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}

优化\(1:\)预处理 $log[N] $数组

for(int i=2;i<=n;i++)
    Log[i]=Log[i-1]+((1<<Log[i-1]+1)==i);

优化\(2:\) \(dfs\)同时预处理 \(f[i][k]\) 数组

----因为深搜时根的数组会先被处理,不会调用到未处理的区域

void dfs(int u,int f) {
    fa[u][0]=f;
    for(int j=1;j<L;j++)
        if(fa[u][j-1]<0)fa[u][j]=-1;
        else fa[u][j]=fa[fa[u][j-1]][j-1];
    for(reg int i=head[u]; i; i=nxt[i]) if(to[i]!=f) {
            reg int &v=to[i],&w=x[i];
            h[v]=h[u]+1;
            dis[v]=dis[u]+w;
            dfs(v,u);
        }
}

整体代码\(Show\)

#include<cstdio>
#include<cstring>
#include <algorithm>
#include<cmath>
using namespace std;
#define reg register
const int N=5e5+10,LN=23;
int n,m,L,st;
int f[N][LN],h[N];
int to[N<<1],head[N<<1],nxt[N<<1],cnt,Log[N];
#define add(u,v) nxt[++cnt]=head[u],head[u]=cnt,to[head[u]]=v
int rd() {
    int s=0;
    char x=getchar();
    while(x<'0'||x>'9')x=getchar();
    while(x>='0'&&x<='9')s=(s<<1)+(s<<3)+(x^'0'),x=getchar();
    return s;
}

void dfs(int u,int fa) {
    f[u][0]=fa;
    for(int j=1;j<L;j++)
        if(f[u][j-1]<0)f[u][j]=-1;
        else f[u][j]=f[f[u][j-1]][j-1];
    for(int i=head[u]; i; i=nxt[i]) if(to[i]!=fa) {
            reg int &v=to[i];
            h[v]=h[u]+1;
            dfs(v,u);
        }
}
void LCA_init() {
    dfs(st,-1);
    for(int i=2;i<=n;i++)
        Log[i]=Log[i-1]+((1<<Log[i-1]+1)==i);
}
int LCA(int x,int y) {
    if(h[x]>h[y])swap(x,y);
    int del=h[y]-h[x];
    for(int i=0; (1<<i)<=del; i++)
        if(del&(1<<i))
            y=f[y][i];
    if(x==y)return x;
    for(int i=Log[h[x]]+1; i>=0; i--)
        if(f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][0];
}
int main() {
    n=rd(),m=rd(),st=rd();
    L=ceil(log(n));
    for(int i=1,u,v,w; i<n; i++)
        u=rd(),v=rd(),add(u,v),add(v,u);
    LCA_init();
    for(int i=1,a,b; i<=m; i++)
        a=rd(),b=rd(),printf("%d\n",LCA(a,b));
}

\(3.\)重链剖分

查询原理:与蜗牛爬类似

实际上,我们可以注意到蜗牛爬式大部分时间的浪费在一个个找上

而我们通过重链剖分使这个过程加快

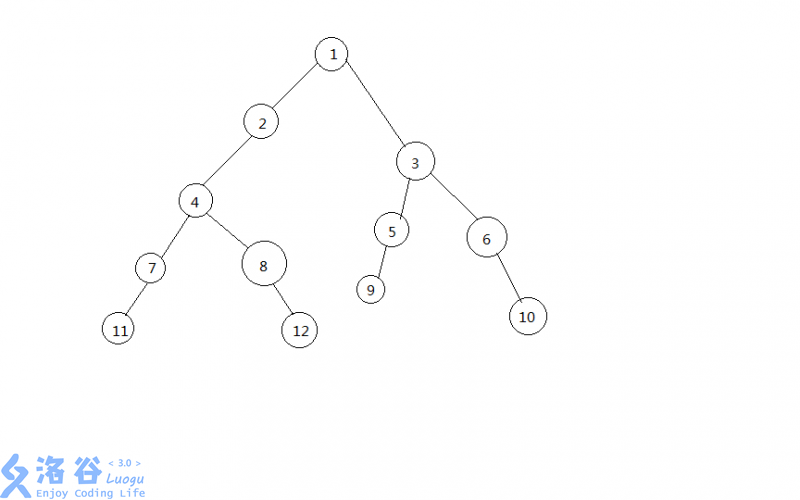
对于查询\(LCA(11,9)\),蜗牛爬式给出的过程是

11,9

7,9

4,5

2,3

1,1

1

一个个爬上去

事实上 \(11-7-4\)的过程可以化为\(11-4\)

同样的 \(4-2-1\) 化为\(4-1\) 等等

这条链越长,其中无用的部分越多,所以把一条条链分出来非常有必要

所以有了重链剖分,这是它的过程

11,9

4,9

4,3

4,1

1

过程简化了不少,当链越长,效果越好

算法核心:

维护\(size[N],son[N],top[N],fa[N],depth[N]\)数组

\(size[N]:\)这个子树的结点数量

\(son[N]:\)这个结点下最重的儿子

\(top[N]:\)这条链的顶端

\(fa[N]:\)这个结点的父亲

\(depth[N]:\)这个节点的深度

这个过程可以在两次深搜内解决

void dfs1(int u,int f) {
    fa[u]=f;
    son[u]=0,size[u]=1;
    for(int i=head[u]; i; i=e[i].nxt) if(e[i].v!=f) {
            int &v=e[i].v;
            depth[v]=depth[u]+1;
            dfs1(v,u);
            if(size[son[u]]<size[v])son[u]=v;
            size[u]+=size[v];
        }
}

这里处理了\(fa[N],son[N],size[N],depth[N]\)数组

也就是说,只剩\(top[N]\)了

void dfs2(int u,int t) {
    top[u]=t;
    if(son[u])dfs2(son[u],t);//把这一条链连到底,top都设成t
    else return;//如果是叶节点就不用找了
    for(int i=head[u]; i; i=e[i].nxt) {
        int &v=e[i].v;
        if(v==f[u]||v==son[u])continue;
        dfs2(v,v);//对于其他的轻链,分开处理,以它自己为top
    }
}

查询部分:

int LCA(int x,int y) {
    while(top[x]!=top[y]) {
        if(depth[top[x]]>depth[top[y]])x=fa[top[x]];
        else y=fa[top[y]];
    }
    return depth[x]<depth[y]?x:y;
}

其实与蜗牛爬式类似,跳过了这条链上的移动过程

\(code\)整体\(Show\)

#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
#define add(__u,__v) e[++cnt].nxt=head[__u],e[head[__u]=cnt].v=__v
#define reg register
inline void rd(reg int &s){
    s=0;
    reg char x=getchar();
    while(x<'0'||x>'9')x=getchar();
    while(x>='0'&&x<='9')s=(s<<1)+(s<<3)+(x^'0'),x=getchar();
}
inline void wt(reg int x){
    reg char buf[10]={0,0},l=0;
    do buf[++l]=x%10;
    while(x/=10);
    if(!l)l=1;
    for(;l;l--)putchar(buf[l]+'0');
}
const int N=1e5+10;
int n,m,st;
int fa[N],head[N<<1],cnt;
struct node {
    int v,nxt;
} e[N<<1];
int depth[N],top[N],son[N],size[N];
void dfs1(int u,int f) {
    fa[u]=f;
    son[u]=0,size[u]=1;
    for(int i=head[u]; i; i=e[i].nxt) if(e[i].v!=f) {
            int &v=e[i].v;
            depth[v]=depth[u]+1;
            dfs1(v,u);
            if(size[son[u]]<size[v])son[u]=v;
            size[u]+=size[v];
        }
}

void dfs2(int u,int t) {
    top[u]=t;
    if(son[u])dfs2(son[u],t);
    else return;
    for(int i=head[u]; i; i=e[i].nxt) {
        int &v=e[i].v;
        if(v==fa[u]||v==son[u])continue;
        dfs2(v,v);
    }
}

int LCA(int x,int y) {
    while(top[x]!=top[y]) {
        if(depth[top[x]]>depth[top[y]])x=fa[top[x]];
        else y=fa[top[y]];
    }
    return depth[x]<depth[y]?x:y;
}

int main() {
    scanf("%d%d%d",&n,&m,&st);
    for(int i=1,u,v; i<n; i++)rd(u),rd(v),add(u,v),add(v,u);
    dfs1(st,0),dfs2(st,st);
    for(int i=1,a,b; i<=m; i++) rd(a),rd(b),wt(LCA(a,b)),putchar('\n');
}