混合高斯模型(Gaussian mixture model, GMM)
1. 前言
这就是为什么我要学习一下二维高斯分布的原因:
总感觉数学知识不够用呐,顺带把混合高斯模型也回顾一下。

2. 单高斯模型(Gaussian single model, GSM)
2.1 一维高斯模型
高斯分布(Gaussian distribution)有时也被称为正态分布(normal distribution),是一种在自然界大量的存在的、最为常见的分布形式。
如果我们对大量的人口进行身高数据的随机采样,并且将采得的身高数据画成柱状图,将会得到如下图1所示的图形。这张图模拟展示了334个成人的统计数据,可以看出图中最多出现的身高在180cm左右2.5cm的区间里。
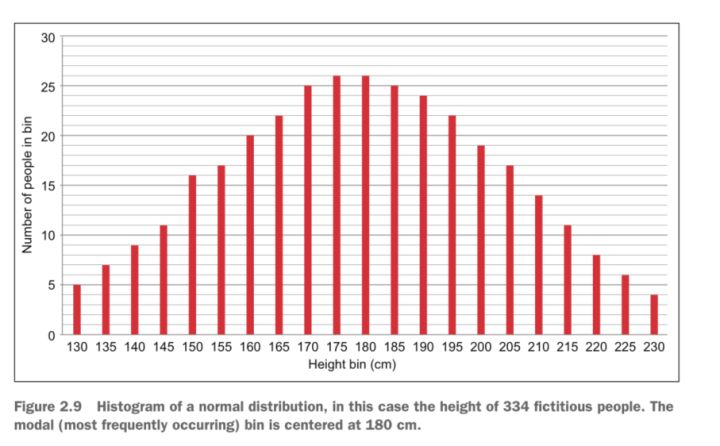
一维高斯分布的概率密度函数如下:

其中 为数据均值(期望),
为数据标准差(Standard deviation)。均值对应正态分布的中间位置,在本例中我们可以推测均值在180cm附近。标准差衡量了数据围绕均值分散的程度。
上面的公式是概率密度函数,也就是在已知参数的情况下,输入变量指x,可以获得相对应的概率密度。还要注意一件事,就是在实际使用前,概率分布要先进行归一化,也就是说曲线下面的面积之和需要为1,这样才能确保返回的概率密度在允许的取值范围内。
如果需要计算指定区间内的分布概率,则可以计算在区间首尾两个取值之间的面积的大小。另外除了直接计算面积,还可以用更简便的方法来获得同样的结果,就是减去区间x对应的累积密度函数(cumulative density function,CDF)。因为CDF表示的是数值小于等于x的分布概率。
3.高斯混合模型(Gaussian mixture model, GMM)
3.1 公式
高斯混合模型是对高斯模型进行简单的扩展,GMM使用多个高斯分布的组合来刻画数据分布。
举例来说:
想象下现在咱们不再考察全部用户的身高,而是要在模型中同时考虑男性和女性的身高。假定之前的样本里男女都有,那么之前所画的高斯分布其实是两个高斯分布的叠加的结果。相比只使用一个高斯来建模,现在我们可以用两个(或多个)高斯分布
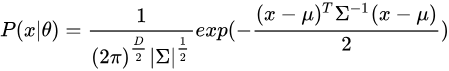
其中, 为数据均值(期望),
为协方差(Covariance),D 为数据维度。
3.2 高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。一般来说,一个混合模型可以使用任何概率分布,这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。
举个不是特别稳妥的例子,比如我们现在有一组狗的样本数据,不同种类的狗,体型、颜色、长相各不相同,但都属于狗这个种类,此时单高斯模型可能不能很好的来描述这个分布,因为样本数据分布并不是一个单一的椭圆,所以用混合高斯分布可以更好的描述这个问题,如下图所示
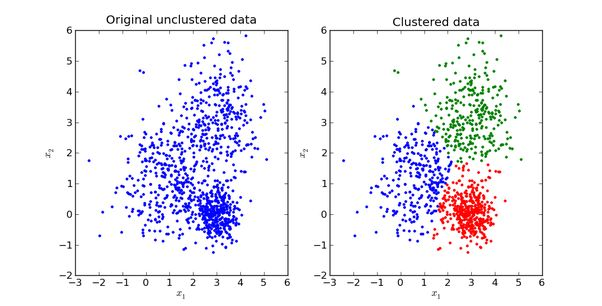
首先定义如下信息:
表示第
个观测数据,
是混合模型中子高斯模型的数量,
是观测数据属于第
个子模型的概率,
,
是第
个子模型的高斯分布密度函数,
。其展开形式与上面介绍的单高斯模型相同
表示第
个观测数据属于第
个子模型的概率
高斯混合模型的概率分布为:
对于这个模型而言,参数 ,也就是每个子模型的期望、方差(或协方差)、在混合模型中发生的概率。
4. 二维高斯分布的参数理解
4.1 均值和协方差矩阵对二维高斯分布的影响
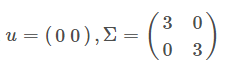
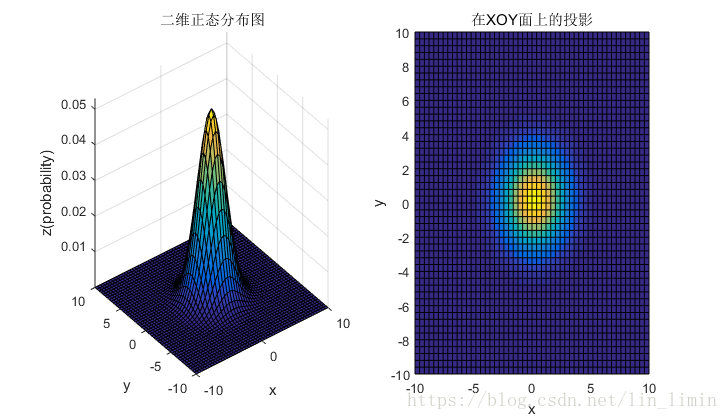

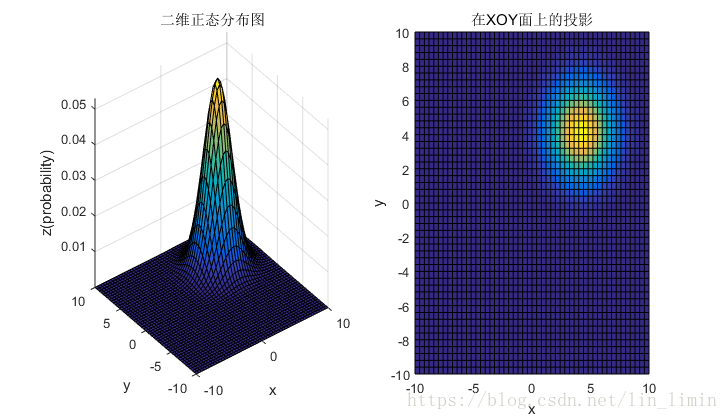

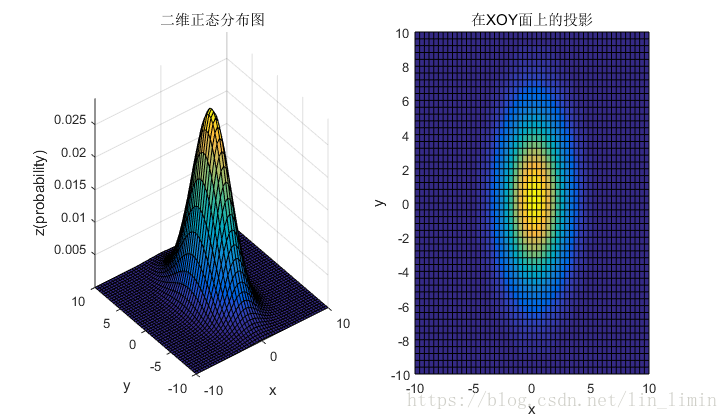
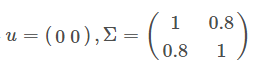
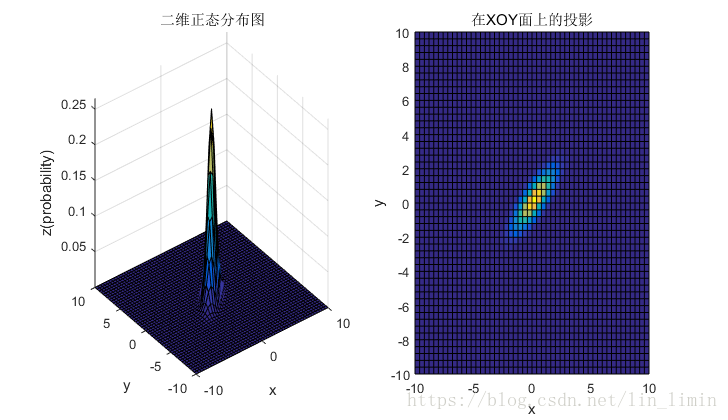
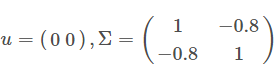
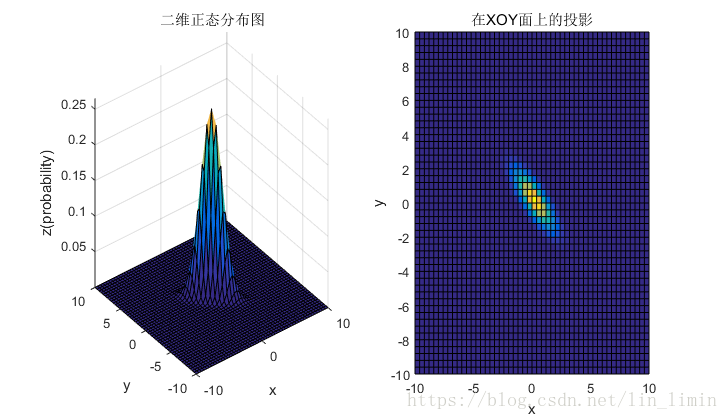
4.2 总结

参考链接:
https://blog.csdn.net/lin_limin/article/details/81024228
https://blog.csdn.net/lin_limin/article/details/81048411
https://zhuanlan.zhihu.com/p/31103654
https://zhuanlan.zhihu.com/p/30483076
混合高斯模型(Gaussian mixture model, GMM)的更多相关文章
- [zz] 混合高斯模型 Gaussian Mixture Model
聚类(1)——混合高斯模型 Gaussian Mixture Model http://blog.csdn.net/jwh_bupt/article/details/7663885 聚类系列: 聚类( ...
- 高斯混合模型Gaussian Mixture Model (GMM)——通过增加 Model 的个数,我们可以任意地逼近任何连续的概率密分布
从几何上讲,单高斯分布模型在二维空间应该近似于椭圆,在三维空间上近似于椭球.遗憾的是在很多分类问题中,属于同一类别的样本点并不满足“椭圆”分布的特性.这就引入了高斯混合模型.——可以认为是基本假设! ...
- 高斯混合模型Gaussian Mixture Model (GMM)
混合高斯模型GMM是指对样本的概率密度分布进行估计,而估计采用的模型(训练模型)是几个高斯模型的加权和(具体是几个要在模型训练前建立好).每个高斯模型就代表了一个类(一个Cluster).对样本中的数 ...
- sklearn聚类模型:基于密度的DBSCAN;基于混合高斯模型的GMM
1 sklearn聚类方法详解 2 对比不同聚类算法在不同数据集上的表现 3 用scikit-learn学习K-Means聚类 4 用scikit-learn学习DBSCAN聚类 (基于密度的聚类) ...
- 混合高斯模型(GMM)推导及实现
作者:桂. 时间:2017-03-20 06:20:54 链接:http://www.cnblogs.com/xingshansi/p/6584555.html 声明:欢迎被转载,不过记得注明出处哦 ...
- 聚类之高斯混合模型(Gaussian Mixture Model)【转】
k-means应该是原来级别的聚类方法了,这整理下一个使用后验概率准确评测其精度的方法—高斯混合模型. 我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussia ...
- 漫谈 Clustering (3): Gaussian Mixture Model
上一次我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussian Mixture Model (GMM).事实上,GMM 和 k-means 很像,不过 GMM ...
- Gaussian Mixture Model
Gaussian Mixture Model (GMM).事实上,GMM 和 k-means 很像,不过 GMM 是学习出一些概率密度函数来(所以 GMM 除了用在 clustering 上之外,还经 ...
- 我自己用C++写了个GMM(Gaussian mixture model)模型
我自己用C++写了个GMM(Gaussian mixture model)模型 Written for an assignment 之前粗粗了解了GMM的原理,但是没有细看,现在有个Assignmen ...
随机推荐
- Spring Cloud Gateway 结合配置中心限流
前言 上篇文章我讲过复杂的限流场景可以通过扩展RedisRateLimiter来实现自己的限流策略. 假设你领导给你安排了一个任务,具体需求如下: 针对具体的接口做限流 不同接口限流的力度可以不同 可 ...
- MySQL的SQL语句——常见报错
Eclipse连接MySQL数据库 — 8.0版jdbc驱动 键知识 https://blog.csdn.net/jenminzhang/article/details/9816853 [必应翻译] ...
- DVWA XSS (Stored) 通关教程
Stored Cross Site Scripting 存储型XSS,持久化,代码是存储在服务器中的,如在个人信息或发表文章等地方,加入代码,如果没有过滤或过滤不严,那么这些代码将储存到服务器中,用户 ...
- Salesforce 开发整理(十一) 自定义放大镜查找效果
有时候在自定义的visualforce页面上,需要实现系统标准的查找样式,当不能使用标准的style的时候,我们只能选择自定义实现,下面分享一个demo,预览效果如下: 实现代码,Visualforc ...
- linux内核动态调试技术
动态调试功能就是你可以决定在程序运行过程中是否要 pr_debug(), dev_dbg(), print_hex_dump_debug(), print_hex_dump_bytes() 这些函数正 ...
- gulp的初阶使用方法(转)
安装好gulp之后接下来就是使用了,此文主要介绍一些前端开发时常用的一些插件及其用法 http://www.imooc.com/article/tag/26/hot/12插件安装 安装本地服务器插件: ...
- 基于hash的AB测试
AB测试 为同一个目标,设计两种方案,将两种方案随机投放市场中,让组成成分相同(相似)用户去随机体验两种方案之一,根据观测结果,判断哪个方案效果更好. 基于hash的AB测试 具体的实现方法为: 在A ...
- POJ 1146 ID Codes 用字典序思想生成下一个排列组合
ID Codes Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 7644 Accepted: 4509 Descript ...
- JSON.parse() 与 JSON.stringify()
JSON.parse() 方法用来解析JSON字符串,构造由字符串描述的JavaScript值或对象.提供可选的reviver函数用以在返回之前对所得到的对象执行变换(操作). 语法 JSON.par ...
- CMake方式编译
[1]CMake基础 CMake是一种跨平台编译工具 CMake主要是编写CMakeLists.txt文件 通过CMake命令将CMakeLists.txt文件转化为make所需的Makefile文件 ...
