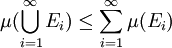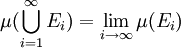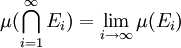测度(Measure)
测度概述
数学上,测度(Measure)是一个函数,它对一个给定集合的某些子集指定一个数,这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的,后来人们希望把积分推广到任意的集合上,就发展出测度的概念,它在数学分析和概率论有重要的地位。
测度论是实分析的一个分支,研究对象有σ代数、测度、可测函数和积分,其重要性在概率论和统计学中有所体现的。
测度的定义
形式上说,一个测度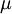 (详细的说法是可列可加的正测度)是个函数。设
(详细的说法是可列可加的正测度)是个函数。设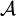 是集合
是集合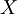 上的一个σ代数,
上的一个σ代数,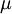 在上
在上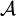 定义,于扩充区间
定义,于扩充区间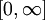 中取值,并且满足以下性质:
中取值,并且满足以下性质:
- 空集的测度为零:
-
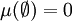 。
。
- 可数可加性,或称σ可加性:若
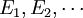 为
为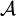 中可数个两两不交的集合的序列,则所有
中可数个两两不交的集合的序列,则所有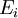 的并集的测度,等于每个
的并集的测度,等于每个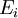 的测度之总和:
的测度之总和:
-
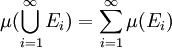 。
。
这样的三元组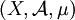 称为一个测度空间,而
称为一个测度空间,而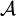 中的元素称为这个空间中的可测集。
中的元素称为这个空间中的可测集。
测度的性质
下面的一些性质可从测度的定义导出:
单调性
测度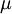 的单调性:
的单调性:
若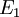 和
和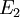 为可测集,而且
为可测集,而且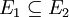 ,则
,则 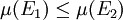 。
。
可数个可测集的并集的测度
若 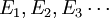 为可测集(不必是两两不交的),并且对于所有的
为可测集(不必是两两不交的),并且对于所有的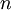 ,
, ⊆
⊆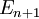 ,则集合
,则集合 的并集是可测的,且有如下不等式(「次可列可加性」):
的并集是可测的,且有如下不等式(「次可列可加性」):
以及如下极限:
可数个可测集的交集的测度
若 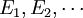 为可测集,并且对于所有的
为可测集,并且对于所有的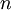 ,
,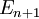 ⊆
⊆ ,则
,则 的交集是可测的。进一步说,如果至少一个
的交集是可测的。进一步说,如果至少一个 的测度有限,则有极限:
的测度有限,则有极限:
如若不假设至少一个 的测度有限,则上述性质一般不成立。例如对于每一个
的测度有限,则上述性质一般不成立。例如对于每一个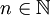 ,令
,令
这里,全部集合都具有无限测度,但它们的交集是空集。
σ有限测度
如果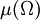 是一个有限实数(而不是
是一个有限实数(而不是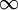 ),则测度空间
),则测度空间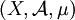 称为有限测度空间。如果
称为有限测度空间。如果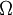 可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合
可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合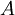 具有σ有限测度,如果
具有σ有限测度,如果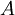 可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
作为例子,实数集赋以标准勒贝格测度是σ有限的,但不是有限的。为说明之,只要考虑闭区间族[k, k+1],k 取遍所有的整数;这样的区间共有可数多个,每一个的测度为1,而且并起来就是整个实数集。作为另一个例子,取实数集上的计数测度,即对实数集的每个有限子集,都把元素个数作为它的测度,至于无限子集的测度则令为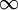 。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
完备性
一个可测集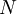 称为零测集,如果
称为零测集,如果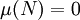 。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
一个测度可以按如下的方式延拓为完备测度:考虑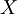 的所有这样的子集
的所有这样的子集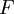 ,它与某个可测集
,它与某个可测集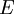 仅差一个可去集,也就是说
仅差一个可去集,也就是说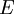 与
与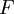 的对称差包含于一个零测集中。由这些子集
的对称差包含于一个零测集中。由这些子集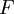 生成的σ代数,并定义
生成的σ代数,并定义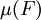 的值就等于
的值就等于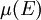 。
。
例子
下列是一些测度的例子(重要性与顺序无关)。
- 计数测度 定义为
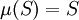 的‘元素个数’。
的‘元素个数’。 - 一维勒贝格测度 是定义在
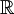 的一个含所有区间的σ代数上的、完备的、平移不变的、满足
的一个含所有区间的σ代数上的、完备的、平移不变的、满足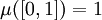 的唯一测度。
的唯一测度。 - Circular angle 测度 是旋转不变的。
- 局部紧拓扑群上的哈尔测度是勒贝格测度的一种推广,而且也有类似的刻划。
- 恆零测度 定义为
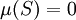 ,对任意的
,对任意的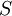 。
。 - 每一个概率空间都有一个测度,它对全空间取值为1(于是其值全部落到单位区间[0,1]中)。这就是所谓概率测度。
- 其它例子,包括:狄拉克测度、波莱尔测度、若尔当测度、遍历测度、欧拉测度、高斯测度、贝尔测度、拉东测度。
测度(Measure)的更多相关文章
- [实变函数]3.1 外测度 (outer measure)
1 并不是所有的集合都可求测度. 我们的想法是先对 $\bbR^n$ 中的任一集合定义一个``外 测度'' (outer measure), 然后再加上适当的条件 (Caratheodory 条件), ...
- 深度学习-Wasserstein GAN论文理解笔记
GAN存在问题 训练困难,G和D多次尝试没有稳定性,Loss无法知道能否优化,生成样本单一,改进方案靠暴力尝试 WGAN GAN的Loss函数选择不合适,使模型容易面临梯度消失,梯度不稳定,优化目标不 ...
- 测度论--长度是怎样炼成的[zz]
http://www.58pic.com/newpic/27882296.html http://www.58pic.com/newpic/27893137.html http://699pic.co ...
- An Introduction to Measure Theory and Probability
目录 Chapter 1 Measure spaces Chapter 2 Integration Chapter 3 Spaces of integrable functions Chapter 4 ...
- Android measure过程分析
作为一名Android开发人员,我们都知道一个View从无到有,会经历3个阶段: 1. measure/测量阶段,也就是确定某个view大小的过程: 2. layout/布局阶段,也就是确定其左上右下 ...
- \(\S1 \) Gaussian Measure and Hermite Polynomials
Define on \(\mathbb{R}^d\) the normalized Gaussian measure\[ d \gamma(x)=\frac{1}{(2\pi)^{\frac{d}{2 ...
- 通过Measure & Arrange实现UWP瀑布流布局
简介 在以XAML为主的控件布局体系中,有用于完成布局的核心步骤,分别是measure和arrange.继承体系中由UIElement类提供Measure和Arrange方法,并由其子类Framewo ...
- 普通View的measure流程
对于普通的view,其测量在ViewGroup中的measureChildWithMargins函数中调用child view的measure开始测量. 1:从measure函数开始 public f ...
- [CareerCup] 16.2 Measure Time in a Context Switch 测量上下文转换的时间
16.2 How would you measure the time spent in a context switch? 上下文转换发生在两个进程之间,比如让一个等待进程进入执行和让一个运行进程进 ...
随机推荐
- [技术博客]利用第三方框架react-native-swipeout实现左右滑动出现按钮
在之前的开发中,为了实现用户不同手势操作能够对应不同的功能,我们考虑使用React-Native的API--PanResponder,实现识别用户的手势,实现不同的功能.但我们很快就发现,这样简单的实 ...
- [Beta]Scrum Meeting#8
github 本次会议项目由PM召开,时间为5月13日晚上10点30分 时长10分钟 任务表格 人员 昨日工作 下一步工作 木鬼 撰写博客整理文档 撰写博客整理文档 swoip 为适应新功能调整布局 ...
- Python3+mitmproxy安装使用教程(Windows)(转载)
mitmproxy 是用于MITM的proxy,MITM中间人攻击.说白了就是服务器和客户机中间通讯多增加了一层.跟Fiddler和Charles最大的不同就是,mitmproxy可以进行二次开发,尤 ...
- OpenTK学习笔记:C#的中开发OpenGL程序的4种开源封包库SharpGL、CsGL、OpenTK、Tao框架的简单对比
最近要在C#的语言环境下开发OpenGL程序,参考了网上的博客论坛http://www.cnblogs.com/hanyonglu/archive/2012/06/12/2546581.html,总结 ...
- Appium脚本(5) 元素等待方法示例
思考 在自动化过程中,元素出现受网络环境,设备性能等多种因素影响.因此元素加载的时间可能不一致,从而会导致元素无法定位超时报错,但是实际上元素是正常加载了的,只是出现时间晚一点而已.那么如何解决这个问 ...
- hashMap的原理
hashMap的原理分析(转载) 1.总结: HashMap是基于哈希表实现的,用Entry[]来存储数据,而Entry中封装了key.value.hash以及Entry类型的next HashMap ...
- Nginx - 安装并启动Nginx
1 - 安装Nginx 官网步骤:http://nginx.org/en/linux_packages.html#RHEL-CentOS [Anliven@h202 ~]$ sudo vim /etc ...
- 右键管理员身份打开 命令行cmd
添加到注册表将下面命令保存为reg文件: Windows Registry Editor Version 5.00 [-HKEY_CLASSES_ROOT\Directory\shell\runas] ...
- 静默安装weblogic12c提示INST-07319: Oracle 主目录(O) 位置的验证失败。指定的位置已存在, 是非空目录并且不是有效的 Oracle 主目录
[xxx@localhost bea12c3]$ java -jar fmw_12.2.1.3.0_wls.jar -silent -responseFile /app/bea12c3/weblogi ...
- DOM事件: DOM事件级别、DOM事件流、DOM事件模型、DOM事件捕获过程、自定义事件
前端面试中只要问到事件,就肯定会有DOM事件:如果回答出来了,就会一直向下延申,其实这些东西都很简单,但我第一次被问到的时候,也是懵的: DOM事件级别: DOM0 element.onclick = ...