[NOIP2017] 逛公园 解题报告(DP)

我很不想说 在我的AC代码上我打了表，但实在没有办法了。莫名的8，9个点RE。然而即便是打表。。。也花了我很久。

这大概是NOIP2017最难的题了，为了让不懂的人更容易理解，这篇题解会比较详细

我的做法是DP，在程序中写的是记忆化搜索，下面我着重讲一下状态转移方程和程序中的一些小细节

SPFA

首先对于每组数据，SPFA直接算出dist[i],表示从节点i到节点n的最短距离。是的没有看错，是到节点n的最短距离，至于为什么呢？我在下面会很详细地讲解。但我们先得完成这个SPFA，很容易，对于题目中给的每一条边反着建，得到另外一张图，姑且叫反向图。（当然原图也还是要建的，叫正向图）

状态设计

设计状态f[u][know]表示在反向图中从节点u到节点n，与从节点u到节点n的最短路径相差等于know的路径数,即可表示为f[u][know]是满足dis(u,n)==MinDis(u,n)+know 的方案数

那么答案就是∑f[1][know] (0<=know<=k)，我们会在程序之中枚举know把每个都算出来

状态转移方程

int sum=;
for (int i=head[u];i!=-;i=edge[i].next)
{
    int tmp=know-(dist[edge[i].to]+edge[i].val-dist[u]);
    if (tmp<||tmp>k) continue;
    sum=(sum+dfs(edge[i].to,tmp))%p;
    if (flag) return ;
}

直接说不好讲，现在对代码进行直接讲解

首先明确，最后sum的值就是f[u][know]的值。tmp表示得是转移到v的新的know的值（know'） 也就是说，我们将状态f[u][know]由f[v][know']转移得到

也就是简单的相加统计方案数了

那么现在进入最重要的环节，这个状态转移方程式怎么推出来的。请看

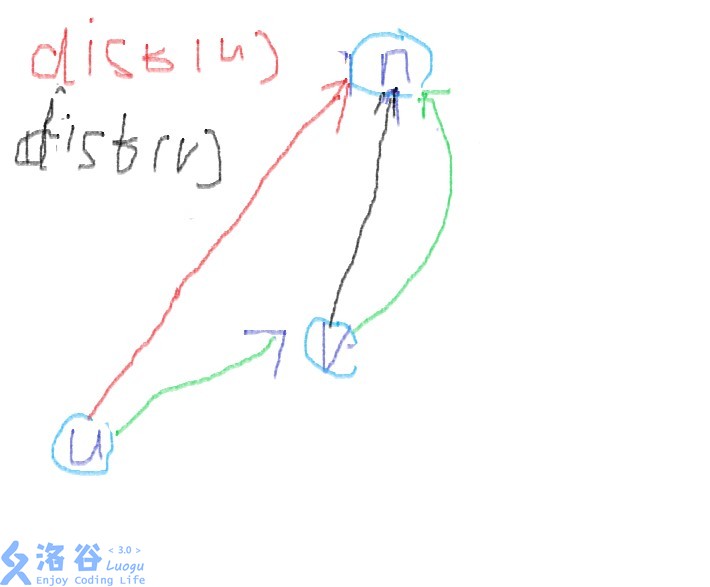
<v,n>(那条绿的)减去黑边(dist[v])就是know' <u,n>（一条绿的加上黑的）减去红边（dist[u]）就是know 这样的话就麻烦读者自己手推一下立马就得到状态转移方程了

方程的初始值就是f[know][0]=1

好的现在解释为什么要建反向图。

因为不是每个节点都能够到达节点n的，毕竟这是有向图，反向建图的好处就是可以完全回避进入死胡同的情况，同时也是为了spfa算出到节点n的值，这是一种常用的技巧。

下面附上代码

#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#define re register int
#define fo(i,a,b) for (re i=a;i<=b;i++)
using namespace std;

const int inf=0x3f;
const int maxn=+;
const int mxn=+;
int T,n,m,k,p,sum1,sum2;
int head[mxn],rev[mxn],dist[mxn],vis[mxn],wd[mxn][+],f[mxn][+];//设f[u][know]为到u点时与从终点开始的最短路的偏移量为know的时候的总方案数目。
bool flag;
struct EDGE
{
    int to,next,val;
}edge[maxn],reve[maxn];
inline int read() {
    char ch = getchar();int ret=;
    while(ch<''||ch >'') ch=getchar();
    while(ch<=''&&ch>='') ret=ret*+ch-'',ch=getchar();
    return ret;
}
void init()
{
    memset(head,-,sizeof(head));
    memset(rev,-,sizeof(rev));
    sum1=;sum2=;
    memset(edge,,sizeof(edge));
    memset(reve,,sizeof(reve));
    memset(f,-,sizeof(f));
    flag=false;
}
void add(int x,int y,int z)
{
    edge[++sum1]=(EDGE){y,head[x],z};
    head[x]=sum1;
}
void addr(int x,int y,int z)
{
    reve[++sum2]=(EDGE){y,rev[x],z};
    rev[x]=sum2;
}
void spfa()
{
    queue <int> q;
    memset(dist,inf,sizeof(dist));
    memset(vis,,sizeof(vis));
    dist[n]=;
    vis[n]=;
    q.push(n);
    while (!q.empty())
    {
        int x=q.front();q.pop();vis[x]=;
        for (int i=rev[x];i!=-;i=reve[i].next)
        if (dist[reve[i].to]>dist[x]+reve[i].val){
            dist[reve[i].to]=dist[x]+reve[i].val;
            if (!vis[reve[i].to])
            {
              vis[reve[i].to]=;
              q.push(reve[i].to);
            }
        }
    }
}
int dfs(int u,int know)
{
    if (wd[u][know]) {flag=true;return ;}
    if (f[u][know]>) return f[u][know];
    wd[u][know]=;
    int sum=;
    for (int i=head[u];i!=-;i=edge[i].next)
    {
        int tmp=know-(dist[edge[i].to]+edge[i].val-dist[u]);
        if (tmp<||tmp>k) continue;
        sum=(sum+dfs(edge[i].to,tmp))%p;
        if (flag) return ;
    }
    if (u==n&&know==) sum=;
    wd[u][know]=;
    return f[u][know]=sum;
}
int main()
{
    T=read();
    while (T--)
    {
    init();
    scanf("%d%d%d%d",&n,&m,&k,&p);
    fo(i,,m)
    {
        int x=read(),y=read(),z=read();
        add(x,y,z);
        addr(y,x,z);
     }
    spfa();
    int ans=;
    fo(i,,k)
    {
    memset(wd,,sizeof(wd));
    ans=(ans+dfs(,i))%p;
}
    if (flag) puts("-1");else printf("%d\n",ans);
    }
    return ;
}

需要注意的有几个点（我自己调试中出现的问题） 1.一定加上快读。。莫名快读比scanf快了5s，怀疑洛谷评测机出了问题 2.memset不要用for循环代替（我看到讨论里有人说用for循环，我用了之后从两个RE变成了三个TLE） 3.记得每次都要初始化

那么就是这样了（省选前交篇题解膜一下）