深度神经网络（DNN）

深度神经网络（Deep Neural Networks，以下简称DNN）是深度学习的基础，而要理解DNN，首先我们要理解DNN模型，下面我们就对DNN的模型与前向传播算法做一个总结。

1. 从感知机到神经网络

　　　　在感知机原理小结中，我们介绍过感知机的模型，它是一个有若干输入和一个输出的模型，如下图:

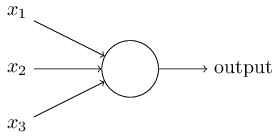
　　　　输出和输入之间学习到一个线性关系，得到中间输出结果：

z=∑i=1mwixi+bz=∑i=1mwixi+b

　　　　接着是一个神经元激活函数:

sign(z)={−11z<0z≥0sign(z)={−1z<01z≥0

　　　　从而得到我们想要的输出结果1或者-1。

　　　　这个模型只能用于二元分类，且无法学习比较复杂的非线性模型，因此在工业界无法使用。

　　　　而神经网络则在感知机的模型上做了扩展，总结下主要有三点：

　　　　1）加入了隐藏层，隐藏层可以有多层，增强模型的表达能力，如下图实例，当然增加了这么多隐藏层模型的复杂度也增加了好多。

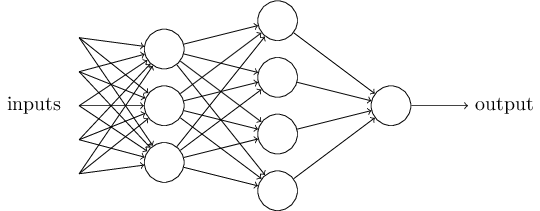
　　　　2）输出层的神经元也可以不止一个输出，可以有多个输出，这样模型可以灵活的应用于分类回归，以及其他的机器学习领域比如降维和聚类等。多个神经元输出的输出层对应的一个实例如下图，输出层现在有4个神经元了。

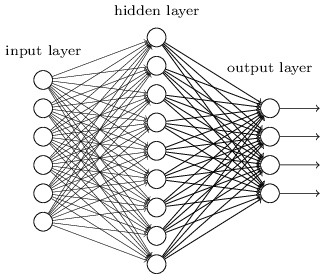
　　　　3）对激活函数做扩展，感知机的激活函数是sign(z)sign(z),虽然简单但是处理能力有限，因此神经网络中一般使用的其他的激活函数，比如我们在逻辑回归里面使用过的Sigmoid函数，即：

f(z)=11+e−zf(z)=11+e−z

　　　　还有后来出现的tanx, softmax,和ReLU等。通过使用不同的激活函数，神经网络的表达能力进一步增强。对于各种常用的激活函数，我们在后面再专门讲。

2. DNN的基本结构

　　　　上一节我们了解了神经网络基于感知机的扩展，而DNN可以理解为有很多隐藏层的神经网络。这个很多其实也没有什么度量标准, 多层神经网络和深度神经网络DNN其实也是指的一个东西，当然，DNN有时也叫做多层感知机（Multi-Layer perceptron,MLP）, 名字实在是多。后面我们讲到的神经网络都默认为DNN。

　　　　从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层,如下图示例，一般来说第一层是输出层，最后一层是输出层，而中间的层数都是隐藏层。

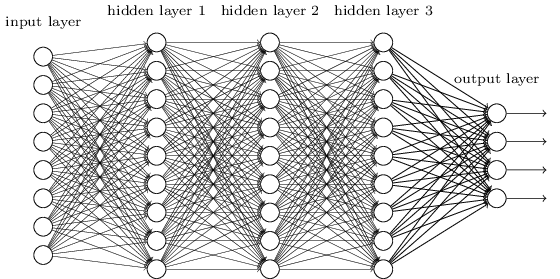
　　　　层与层之间是全连接的，也就是说，第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂，但是从小的局部模型来说，还是和感知机一样，即一个线性关系z=∑wixi+bz=∑wixi+b加上一个激活函数σ(z)σ(z)。

　　　　由于DNN层数多，则我们的线性关系系数ww和偏倚bb的数量也就是很多了。具体的参数在DNN是如何定义的呢？

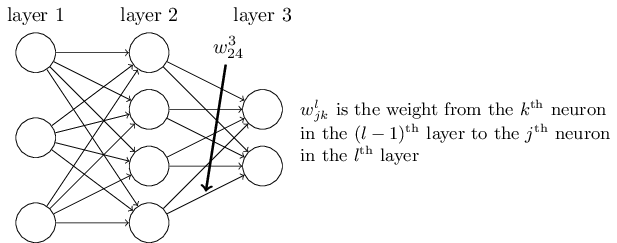
　　　　首先我们来看看线性关系系数ww的定义。以下图一个三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的线性系数定义为w324w243。上标3代表线性系数ww所在的层数，而下标对应的是输出的第三层索引2和输入的第二层索引4。你也许会问，为什么不是w342w423, 而是w324w243呢？这主要是为了便于模型用于矩阵表示运算，如果是w324w243而每次进行矩阵运算是wTx+bwTx+b，需要进行转置。将输出的索引放在前面的话，则线性运算不用转置,即直接为wx+bwx+b。总结下，第l−1l−1层的第k个神经元到第ll层的第j个神经元的线性系数定义为wljkwjkl。注意，输入层是没有ww参数的。

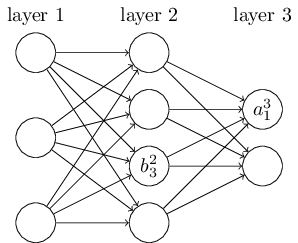
　　　　再来看看偏倚bb的定义。还是以这个三层的DNN为例，第二层的第三个神经元对应的偏倚定义为b23b32。其中，上标2代表所在的层数，下标3代表偏倚所在的神经元的索引。同样的道理，第三个的第一个神经元的偏倚应该表示为b31b13。同样的，输入层是没有偏倚参数bb的。

3. DNN前向传播算法数学原理

　　　　在上一节，我们已经介绍了DNN各层线性关系系数ww,偏倚bb的定义。假设我们选择的激活函数是σ(z)σ(z)，隐藏层和输出层的输出值为aa，则对于下图的三层DNN,利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。

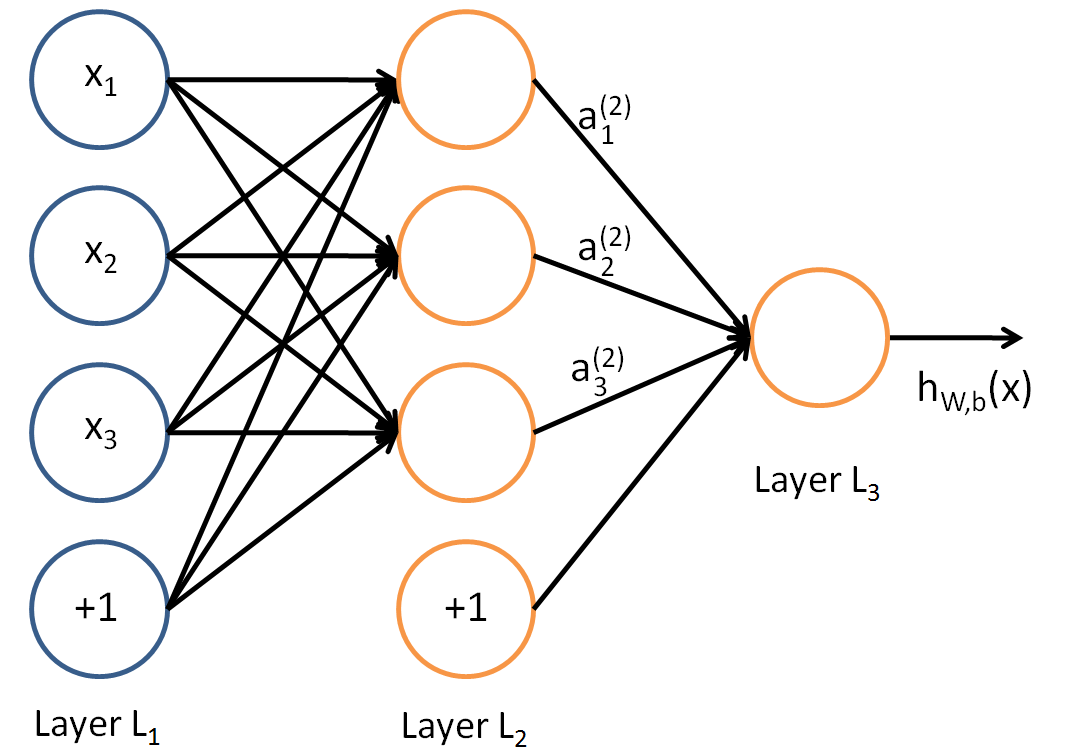
　　　　对于第二层的的输出a21,a22,a23a12,a22,a32，我们有：

a21=σ(z21)=σ(w211x1+w212x2+w213x3+b21)a12=σ(z12)=σ(w112x1+w122x2+w132x3+b12)

a22=σ(z22)=σ(w221x1+w222x2+w232x3+b22)a22=σ(z22)=σ(w212x1+w222x2+w322x3+b22)

a23=σ(z23)=σ(w231x1+w232x2+w233x3+b23)a32=σ(z32)=σ(w312x1+w322x2+w332x3+b32)

　　　　对于第三层的的输出a31a13，我们有：

a31=σ(z31)=σ(w311a21+w312a22+w313a23+b33)a13=σ(z13)=σ(w113a12+w123a22+w133a32+b33)

　　　　将上面的例子一般化，假设第l−1l−1层共有m个神经元，则对于第ll层的第j个神经元的输出aljajl，我们有：

alj=σ(zlj)=σ(∑k=1mwljkal−1k+blj)ajl=σ(zjl)=σ(∑k=1mwjklakl−1+bjl)

　　　　其中，如果l=2l=2,则对于的a1kak1即为输入层的xkxk。

　　　　从上面可以看出，使用代数法一个个的表示输出比较复杂，而如果使用矩阵法则比较的简洁。假设第l−1l−1层共有m个神经元，而第ll层共有n个神经元，则第ll层的线性系数ww组成了一个n×mn×m的矩阵WlWl, 第ll层的偏倚bb组成了一个n×1n×1的向量blbl , 第l−1l−1层的的输出aa组成了一个m×1m×1的向量al−1al−1，第ll层的的未激活前线性输出zz组成了一个n×1n×1的向量zlzl, 第ll层的的输出aa组成了一个n×1n×1的向量alal。则用矩阵法表示，第l层的输出为：

al=σ(zl)=Wlal−1+blal=σ(zl)=Wlal−1+bl

　　　　这个表示方法简洁漂亮，后面我们的讨论都会基于上面的这个矩阵法表示来。

4. DNN前向传播算法

　　　　有了上一节的数学推导，DNN的前向传播算法也就不难了。所谓的DNN的前向传播算法也就是利用我们的若干个权重系数矩阵WW,偏倚向量bb来和输入值向量xx进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。

　　　　输入: 总层数L，所有隐藏层和输出层对应的矩阵WW,偏倚向量bb，输入值向量xx

　　　　输出：输出层的输出aLaL

　　　　1）初始化a1=xa1=x

　　　　2) for l=2l=2 to LL, 计算：

al=σ(zl)=Wlal−1+blal=σ(zl)=Wlal−1+bl

　　　　最后的结果即为输出aLaL。

5. DNN前向传播算法小结

　　　　单独看DNN前向传播算法，似乎没有什么大用处，而且这一大堆的矩阵WW,偏倚向量bb对应的参数怎么获得呢？怎么得到最优的矩阵WW,偏倚向量bb呢？这个我们在讲DNN的反向传播算法时再讲。而理解反向传播算法的前提就是理解DNN的模型与前向传播算法。这也是我们这一篇先讲的原因。

（欢迎转载，转载请注明出处。欢迎沟通交流： pinard.liu@ericsson.com）

参考资料：

1） Neural Networks and Deep Learning by By Michael Nielsen

2） Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville

3） UFLDL Tutorial