tsp问题——遗传算法解决

TSP问题最简单的求解方法是枚举法。

它的解是多维的、多局部极值的、趋于无穷大的复杂解的空间。搜索空间是n个点的全部排列的集合。大小为（n-1）！

。能够形象地把解空间看成是一个无穷大的丘陵地带，各山峰或山谷的高度即是问题的极值。求解TSP，则是在此不能穷尽的丘陵地带中攀登以达到山顶或谷底的过程。

这一篇将用遗传算法解决TSP问题。

1）评价。

这个评价算法应该比較简单了，就是找计算总距离，小的为优。目标函数转化为适应度函数能够取倒数。

2）突变。为了防止反复訪问，不能随机的进行突变。由于每一个城市仅仅能訪问一次。我们仅仅须要随意的交换两个城市就可以。

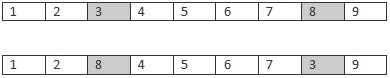
上一行是突变之前。以下一行是突变之后的。

3）交叉。这个操作是个比較关键的步骤。如何交叉才干才干父母的优秀基因呢？对于TSP问题，我们要找的是一个最优的排列。当中排列的顺序应该是最重要的。

因此在交叉的时候。分别随机的取 父母的部分序列，要保持原有的顺序。

Parents

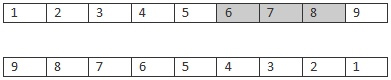
先随机的选取 Parent1 的 一部分。比如 678 部分，。然后把剩下的城市 安装 Parent2 中的顺序，遗传下去。

Chlid

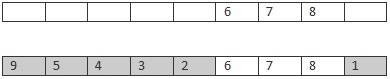
其他基本依照遗传算法的框架来即可了

// TSP.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include<iostream>
//#include <stdio.h>
#include <time.h>
//#include <stdlib.h>

using namespace std;
#define   POPSIZE      200   //种群总数
#define rdint(i)(rand()%(int)(i))
#define rdft()((float)rdint(16384)/(16383.0))
typedef unsigned char BYTE;

//31个城市的坐标
int city[31][2] = { { 1304, 2312 }, 3639, 1315, 4177, 2244, 3712, 1399, 3488, 1535, 3326, 1556, 3238, 1229,
4196, 1004, 4312, 790, 4386, 570, 3007, 1970, 2562, 1756, 2788, 1491, 2381, 1676, 1332, 695, 3715, 1678,
3918, 2179, 4061, 2370, 3780, 2212, 3676, 2578, 4029, 2838, 4263, 2931, 3429, 1908, 3507, 2367, 3394, 2643,
3439, 3201, 2935, 3240, 3140, 3550, 2545, 2357, 2778, 2826, 2370, 2975 };

int* my_unrepeat_rand(int L, int H)
{
	const int LEN = H - L + 1;
	//int n[LEN];
	int *n = new int[LEN];
	for (int i = 0; i < LEN; ++i)
	{
		n[i] = L + i;
	}

	for (int j = LEN; j > 0; --j)
	{
		int m = j*rand() /(RAND_MAX + 1.0);
		int temp = n[m];
		n[m] = n[j - 1];
		n[j - 1] = temp;
	}
	return n;
}

class Chromosome
{
	friend class Population;
public:
	static const int length = 31;

private:
	BYTE gene[length];
	double fitness;
	double distance;
public:
	void initial_chromosome()//初始化染色体
	{
		distance = 0;
		fitness = 0;
		int*b = my_unrepeat_rand(0, length - 1);
		for (int i = 0; i < length; i++)
			gene[i] = b[i];
		delete[]b;
	}
	BYTE*get_gene()
	{
		return this->gene;
	}
	double get_distance()
	{
		return distance;
	}
	void calculate_distance()//计算适应度。这里直接取总距离，越小越好
	{
		distance = 0;
		for (int i = 0; i < length - 1; i++)
		{
			distance += sqrt(pow(double(city[gene[i]][0] - city[gene[i + 1]][0]), double(2)) +
				pow(double(city[gene[i]][1] - city[gene[i + 1]][1]), double(2)));
		}
		distance += sqrt(pow(double(city[gene[0]][0] - city[gene[length - 1]][0]), double(2)) + pow(double(city[gene[0]][1] - city[gene[length - 1]][1]), double(2)));
	}

	pair<Chromosome, Chromosome> cross(Chromosome p1)//交叉操作，选中区间的基因不改变。孩子基因的其它位置的基因从配偶处获得，要保持顺序
	{
		pair<Chromosome, Chromosome>child;
		//srand(time(0));
		int m = rand() % length ;
		int n = rand() % length;
		if (m > n)
		{
			int temp = m;
			m = n;
			n = temp;
		}
		int j = 0,p=0;
		for (int i = 0; i < length; i++)
		{
			if (i >= m&&n >= i)
			{
				child.first.gene[i] = gene[i];
				child.second.gene[i] = p1.gene[i];
				continue;
			}
			bool flag = true;
			while (flag)
			{
				flag = false;
				for (int k = m; k <= n; k++)
					if (p1.gene[j] == gene[k])
					{
					flag = true;
					break;
					}
				if (flag)
					j++;
			}
			child.first.gene[i] = p1.gene[j];
			j++;
			flag = true;
			while (flag)
			{
				flag = false;
				for (int k = m; k <= n; k++)
					if (gene[p] == p1.gene[k])
					{
					flag = true;
					break;
					}
				if (flag)
					p++;
			}
			child.second.gene[i] = gene[p];
			p++;
		}

		return child;
	}

	Chromosome mutation()//变异。选择两个位置交换基因
	{
		int m = rand() % (length - 1);
		int n = rand() % (length - 1);
		while (n == m)
		{
			n = rand() % (length - 1);
		}
		int temp = gene[m];
		gene[m] = gene[n];
		gene[n] = temp;
		return *this;
	}

};

class Population
{
private:
	Chromosome pop[POPSIZE];
	Chromosome best;
	Chromosome worst;
	unsigned int Generation;
	unsigned int maxgeneration;
	double m_dCrossoverRate;//交叉率0.6
	double m_dMutationRate;//变异率0.01
	bool elitism;//是否在新一代中保存前一代的最优个体
	double m_dTotalFitnessScore;
	void initial_pop()
	{
		for (int i = 0; i < POPSIZE; i++)
			pop[i].initial_chromosome();
	};
public:
	Population(double pc, double pM, bool ISelitism, unsigned int maxgen) :m_dCrossoverRate(pc), m_dMutationRate(pM), elitism(ISelitism), maxgeneration(maxgen)//构造函数
	{
		Generation = 1;
		initial_pop();
	}
	void Calcu_fit()//计算适应值
	{
		m_dTotalFitnessScore = 0;
		for (int i = 0; i < POPSIZE; i++)
		{
			pop[i].calculate_distance();
		}
		find_best_worst();
		//sort_by_distance(POPSIZE);
		double mindis = best.distance;
		double maxdis = worst.distance;
		for (int i = 0; i < POPSIZE; i++)
		{
			pop[i].fitness = 1 - (pop[i].distance - mindis) / (maxdis - mindis + 0.0001);//double(1000) / pop[i].distance;//
			m_dTotalFitnessScore += pop[i].fitness;
		}

	}
	//fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.0001)))
	void sort_by_distance(int k)
	{
		if (k == 1)
			return;
		for (int i = 0; i < k-1; i++)
		{
			if (pop[i].distance < pop[i + 1].distance)
			{
				double temp = pop[i].distance;
				pop[i].distance = pop[i + 1].distance;
				pop[i + 1].distance = temp;
			}
		}
		sort_by_distance(k - 1);
	}
	void find_best_worst()
	{
		double mindis = 100000000;
		double maxdis = 0;
		for (int i = 0; i < POPSIZE; i++)
		{
			if (pop[i].distance > maxdis)
			{
				maxdis = pop[i].distance;
				worst = pop[i];
			}
			if (pop[i].distance < mindis)
			{
				mindis = pop[i].distance;
				best = pop[i];
			}
		}
	}

	int RouletteWheelSelection()
	{
		double fSlice = rdft() * m_dTotalFitnessScore;
		double cfTotal = 0.0;

		for (int i = 0; i<POPSIZE; ++i)
		{
			cfTotal += pop[i].fitness;
			if (cfTotal > fSlice)
			{
				return i;
			}
		}
	}
	void Epoch()
	{
		Calcu_fit();
		Chromosome new_pop[POPSIZE+1];
		int NewBabies = 0;
		if (elitism)
		{
			NewBabies = 1;
			new_pop[0] = best;
		}

		while (NewBabies < POPSIZE)
		{
			//select 2 parents
			int mum = RouletteWheelSelection();
			int dad = RouletteWheelSelection();
			while (dad == mum)
			{
				dad = RouletteWheelSelection();
			}pair<Chromosome, Chromosome>child;
			if (rdft() < m_dCrossoverRate)
			{
				child = pop[mum].cross(pop[dad]);
			}
			else
			{
				child.first = pop[mum];
				child.second = pop[dad];
			}
			if (rdft() < m_dMutationRate)
			{
				child.first.mutation();
			}
			if (rdft() < m_dMutationRate)
			{
				child.second.mutation();
			}
			new_pop[NewBabies]=child.first;
			new_pop[NewBabies+1] = child.second;
			NewBabies += 2;
		}

		for (int i = 0; i < POPSIZE; i++)
			pop[i] = new_pop[i];
		++Generation;
	}

	Chromosome get_best()
	{
		return best;
	}
	void run()
	{
		while (Generation < maxgeneration)
		{
			Epoch();
		}
	}

};

int _tmain(int argc, _TCHAR* argv[])
{
	time_t t;
	srand((unsigned)time(&t));

	Population tsp(0.6,0.1,true,1000);
	tsp.run();

	cout << tsp.get_best().get_distance()<<endl;
	system("pause");
	return 0;
}