算法导论————EXKMP

【例题传送门：caioj1461】

---

【EXKMP】最长共同前缀长度

【题意】
给出模板串A和子串B，长度分别为lenA和lenB，要求在线性时间内，对于每个A[i](1<=i<=lenA)，求出A[i..lenA]与B的最长公共前缀长度
【输入文件】
输入A，B两个串，（lenB<=lenA<=1000000) 
【输出文件】
输出lenA个数，表示A[i...lenA]与B的最长公共前缀长度，每个数之前有空格 
【样例输入】
aabbabaaab
aabb
【样例输出】
4 1 0 0 1 0 2 3 1 0

---

算法分析：

　　学EXKMP前，必须将KMP学透，如果仍未学KMP，请出门左转【传送门】

　　我们在KMP算法中可以理解，p数组是KMP的核心，p[i]代表着以i为结尾和以开头为首的最长公共子串长度，也就是说对于st字符串数组的p[i]代表的就是st字符串数组从1开始到p[i]和从i-p[i]+1到i是完全相同的（st[1...p[i]]=st[i-p[i]+1...i]）

　　那么扩展KMP就高级了。一样还是p数组（还是原来的配方，还是熟悉的味道！），但是既然是扩展KMP就不要用p，我就改成extend数组了，表示的意义与普通KMP就大有不同。extend[i]表示的是以i为首和以开头为首的最长前缀，也就是说对于st字符串数组中的extend[i]表示的就是st字符串数组从1开始到extend[i]和从i到i+extend[i]-1是完全相同的（st[1...extend[i]]=st[i...i+extend[i]-1]）

　　首先extend[1]就不用说了，直接等于len这个没有问题吧，那么因为extend[1]这个是具有一定性，所以我们基本把这东西废掉..那么我们就直接从extend[2]开始。然后我们就定义一个k，这个k表示的就是在当前搜索过的范围以内（因为这是线性算法，所以是从1到len）能到达最远（也就是说k+extend[k]-1最大的）的编号，为什么要定义一个这样子的东西，等下你们就知道了。

　　我们先定义一个p，让它等于k+extend[k]-1，那么由extend这个数组的定义我们就可以得到一个等式：st[1...extend[k]]=st[k...p]。因为p=k+extend[k]-1，所以我们又可以得到一条等式：extend[k]=p-k+1，把这个代换到上一条等式上，就会——瞬间爆炸！（好吧开个玩笑..）就会变成：st[1...p-k+1]=st[k...p]，如下图：

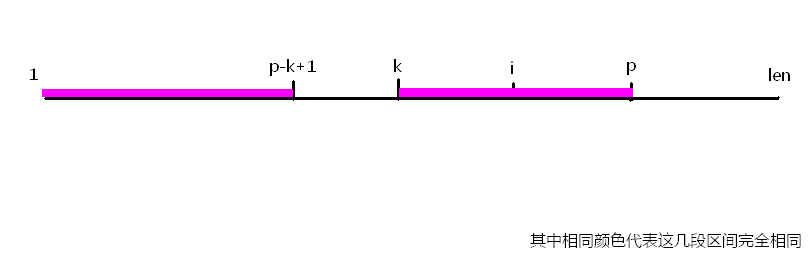
　　　因为我们现在要求从extend[i]，那么由上面这条等式又可以得到另一条等式：st[i-k+1...p-k+1]=st[i...p]，如下图：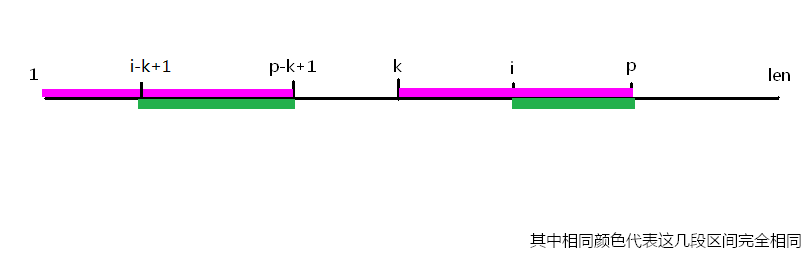

　　在看此证明过程中请各位一直记住extend数组所表达的含义，不然会有很多地方不懂的。那么我们再定义一个L=extend[i-k+1]，我们又可以得到一条等式：st[i-k+1...i-k+L]（注意：本来得到的应该是i-k+1+L-1，我直接把+1-1省略了）=st[1...L]，如下图：

　　这个时候有人就会问了：为什么你上面的图不和前几个合在一起呢？这个就是本算法的一个难点了！因为L的不定性，这个时候我们需要考虑i-k+L和p-k+1的大小！那我们就来分开来考虑。

　　（1）i-k+L<p-k+1，如下图：

　　从上图我们可以看到因为st[1...L]=st[i-k+1...i-k+L]，st[i-k+1...p-k+1]=st[i...p]，所以在st[i...p]中肯定含有一段（从i开始）和st[1...L]是完全相同的，也就是上图标出来的蓝色部分st[i...i+L-1]。因为st[i-k+1...p-k+1]=st[i...p]又因为i-k+L<p-k+1，所以我们又可以得到：st[i-k+L+1]=st[i+L]（也就是上图所标的黄色位置），而因为extend[i-k+1]的定义，所以st[L+1]（也就是上图所标棕色位置）!=st[i-k+L+1]，所以我们可以得到：st[i+L]!=st[L+1]，那么extend[i]就直接等于L了。

　　（2）i-k+L>p-k+1，如下图：

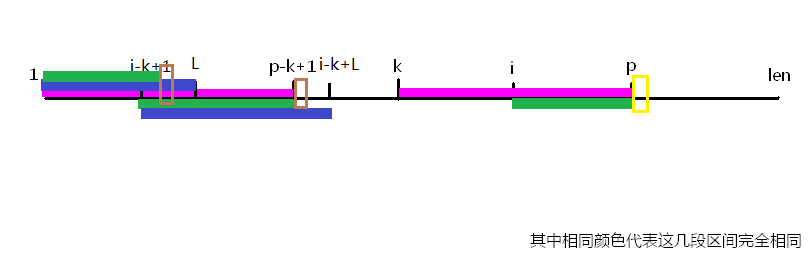
　　从上图中我们看到因为st[1...L]=st[i-k+1...i-k+L]，又因为i-k+L>p-k+1，所以在st[1...L]中肯定含有一段和st[i-k+1...p-k+1]完全相同的（图中绿色部分）。因为extend[k]的意义，所以st[p+1]!=st[p-k+2]（图中第二个棕色和黄色位置，为什么不相同不用解释吧），又因为st[1...L]=st[i-k+1...i-k+L]，所以st[p-i+2]（图中并未标出，第一个棕色位置）=st[p-k+2]，那么就会得到：st[p-i+2]!=st[p+1]，所以extend[i]就等于p-i+1了。

　　（3）i-k+L=p-k+1，如下图：

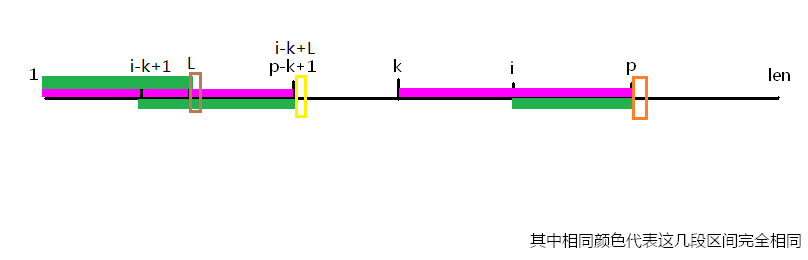
　　从上图我们可以发现因为st[i-k+1...i-k+L]=st[1..L]，st[i-k+1...p-k+1]=st[i...p]，又因为i-k+L=p-k+1，所以st[1...L]=st[i-k+1...p-k+1（可换成i-k+L）]=st[i...p]（也就是指上图中三段绿色部分）。那么由于extend[i-k+1]和extend[k]的意义表达，我们可以得到：st[L+1]!=st[i-k+L+1]，st[i-k+L+1]!=st[p+1]，但是我们不能确定st[L+1]和st[p+1]是否相同，我们只能确定从i开始和从1开始有p-i+1这么长的公共前缀但并不一定是最长的（这句话要好好理解，这很重要）。

　　那么我们就设一个变量j=p-i+1，表示当前从i开始和从1开始的公共前缀长度，由于上面加粗的那句话，我们可以直接从st[j+1]和st[i+j]来累加j的值来得出最长的公共前缀。

　　注意事项：

　　因为p是一个不定的数（由k和extend[k]来定），所以说有可能p-i+1是有可能为负数，那么第二种情况显然不对，公共前缀怎么样也不能等于负数吧，最小也会是0吧！这个时候也许你就会冒出一个想法，在第二种情况下取p-i+1和0的最大值。很显然这是不对的。请看下图：

　　从上图我们可以发现，因为p-i+1是负数，所以上面所有条件都用不了，因为对i后面的字符没有作任何的计算，但这个时候是绝对不可以肯定st[1]和st[i]是不同的（也就是最长公共前缀为0），那么我们需要从st[1]和st[i]开始继续判断后面的字符是否相同。于是我们把第二种情况和第三种情况归纳为一种情况，因为两者都是要暴力处理未知的点，只是起始点不同

　　这仅仅是求extend数组的证明，也仅仅是在同一个字符串里的基本操作，接下来我就来讲下扩展KMP（简称EXKMP）的实际用途。EXKMP主要是利用于解决处理两个字符串的最长公共前缀长度，假如A是主串，B是副串，那么这时我们定义一个ex数组，ex[i]就表示A[i...Alen]和B[1...Blen]的最长公共前缀长度（这个概念需要好好注意）

　　其实在处理两者的匹配时，只需要注意将A串中的子串转移到B串中进行处理，那么这样我们实际上在求ex数组时，操作仍与上面的步骤相似

---

参考代码：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
char sa[],sb[];
int lena,lenb;
int p[],ex[];
//p数组是用来让B串自己匹配自己的
void exkmp()
{
    p[]=lenb;
    int x=;
    while(sb[x]==sb[x+]&&x+<=lenb) x++;//因为我们p[1]是具有一定性，所以我们不能直接用，所以要先暴力求出p[2]
    p[]=x-;
    int k=;
    for(int i=;i<=lenb;i++)
    {
        int pp=k+p[k]-,L=p[i-k+];//pp实际上是p
        if(i+L<pp+) p[i]=L;//i-k+L<pp-k+1化简后i+L<pp
        else
        {
            int j=pp-i+;
            if(j<) j=;
            while(sb[j+]==sb[i+j]&&i+j<=lenb) j++;
            p[i]=j;
            k=i;
        }
    }
    x=;
    while(sa[x]==sb[x]&&x<=lenb) x++;//ex[1]并不具有一定性，所以我们暴力求出ex[1]
    ex[]=x-;
    k=;
    for(int i=;i<=lena;i++)
    {
        int pp=k+ex[k]-,L=p[i-k+];
        if(i+L<pp+) ex[i]=L;
        else
        {
            int j=pp-i+;
            if(j<) j=;
            while(sb[j+]==sa[i+j]&&i+j<=lena&&j<=lenb) j++;
            ex[i]=j;
            k=i;
        }
    }
}
int main()
{
    scanf("%s%s",sa+,sb+);
    lena=strlen(sa+);lenb=strlen(sb+);
    exkmp();
    for(int i=;i<lena;i++) printf("%d ",ex[i]);
    printf("%d\n",ex[lena]);
    return ;
}