曲线生成与求交—B样条曲线

B样条曲线生成

Bezier曲线缺点：改变任一控制点的位置，将影响整条曲线的形状。

B样条曲线是对Bezier曲线的改进，可进行局部控制，生成的曲线与控制多边形的外形更接近，将Bezier曲线作为一特例。

三次B样条曲线的矩阵表达式

\[\begin{aligned}P(t) &= \frac 1 6 \begin{bmatrix} t^3 & t^2 &t & 1\end{bmatrix}\begin{bmatrix}-1 & 3 & -3 & 1\\ 3& -6 & 3 & 0\\ -3 & 0 & 0 & 0\\ 1& 4& 1& 0\end{bmatrix} \begin{bmatrix} P_0 \\ P_1 \\P_2 \\ P_3\end{bmatrix}\quad 0\le t \le 1\end{aligned}
\]

\[\begin{aligned}P'(t) &= \frac 1 2 \begin{bmatrix} t^2 &t & 1\end{bmatrix}\begin{bmatrix}-1 & 3 & -3 & 1\\ 2& -4 & 2 & 0\\ -1 & 0 & 1& 0\end{bmatrix} \begin{bmatrix} P_0 \\ P_1 \\P_2 \\ P_3\end{bmatrix}\end{aligned}
\]

\[\begin{aligned}P''(t) &= \begin{bmatrix} t & 1\end{bmatrix}\begin{bmatrix}-1 & 3 & -3 & 1\\ 1& -2 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} P_0 \\ P_1 \\P_2 \\ P_3\end{bmatrix}\end{aligned}
\]

根据以上三式，得

\[P(0)=\frac 16 (P_0+4P_1+P_2)
\]

\[P(1)=\frac 16 (P_1+4P_2+P_3)
\]

\[ P’(0)=\frac 1 2(P_2-P_0)
\]

\[P’(1)=\frac 1 2(P_3-P_1)
\]

\[P’’(0)= P_0-2P_1+P_2
\]

\[P’’(1)= P_1-2P_2+P_3
\]

起点\(P(0)\)和终点\(P(1)\)不在特征多边形的顶点上。

\(P’(0)\)平行于\(P_0P_2\) ，\(P’(1)\)平行于\(P_1P_3\)

Bezier曲面

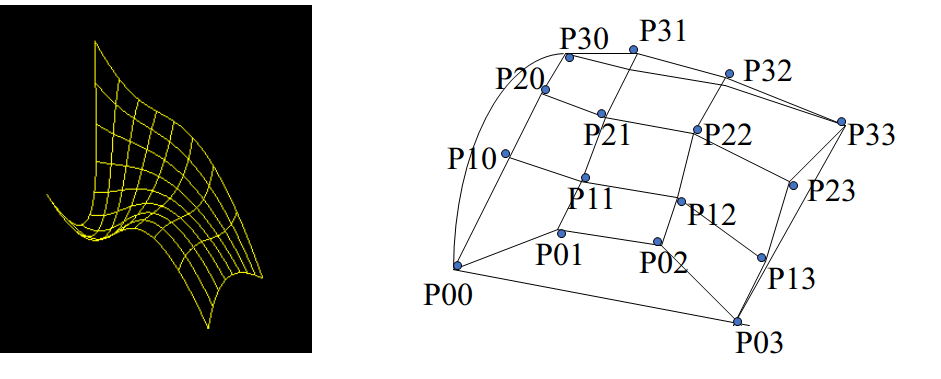
讨论双三次Bezier曲面，通过给顶的\(4\times 4\)个空间网格点来控制的。16个控制点决定了Bezier曲面的形状。

将16 个控制点写成矩阵：

\[B=
\begin{bmatrix}
P_{00} & P_{01} & P_{02} & P_{03}\\
P_{10} & P_{11} & P_{12} & P_{13}\\
P_{20} & P_{21} & P_{22} & P_{23}\\
P_{30} & P_{31} & P_{32} & P_{33}
\end{bmatrix}
\]

Bezier曲面的表达式为：

\[r(u,w)=U\cdot N\cdot B\cdot N^T\cdot W^T\qquad 0≤u≤1, 0≤w≤1
\]

写成x，y，z三个方向分量的形式，则Bezier曲面可表示为：

\[x(u,w)=U\cdot N\cdot B_x\cdot N^T\cdot W^T
\]

\[y(u,w)=U\cdot N\cdot B_y\cdot N^T\cdot W^T
\]

\[z(u,w)=U\cdot N\cdot B_z\cdot N^T\cdot W^T
\]

\[0≤u≤1, 0≤w≤1
\]