Pytorch_第九篇_神经网络中常用的激活函数

神经网络中常用的激活函数

---

Introduce

理论上神经网络能够拟合任意线性函数，其中主要的一个因素是使用了非线性激活函数（因为如果每一层都是线性变换，那有啥用啊，始终能够拟合的都是线性函数啊）。本文主要介绍神经网络中各种常用的激活函数。

以下均为个人学习笔记，若有错误望指出。

---

各种常用的激活函数

早期研究神经网络常常用sigmoid函数以及tanh函数（下面即将介绍的前两种），近几年常用ReLU函数以及Leaky Relu函数（下面即将介绍的后两种）。对于各个激活函数，以下分别从其函数拱墅、函数图像、导数图像以及优缺点来进行介绍。

(1) sigmoid 函数:

sigmoid函数是早期非常常用的一个函数，但是由于其诸多缺点现在基本很少使用了，基本上只有在做二分类时的输出层才会使用。

sigmoid 的函数公式如下：

\[sigmoid(x) = {1 \over (1+exp(-x))}
\]

sigmoid函数的导数有一个特殊的性质（导数是关于原函数的函数），导数公式如下：

\[sigmoid'(x) = sigmoid(x)*(1-sigmoid(x))
\]

sigmoid 的函数图形如下：

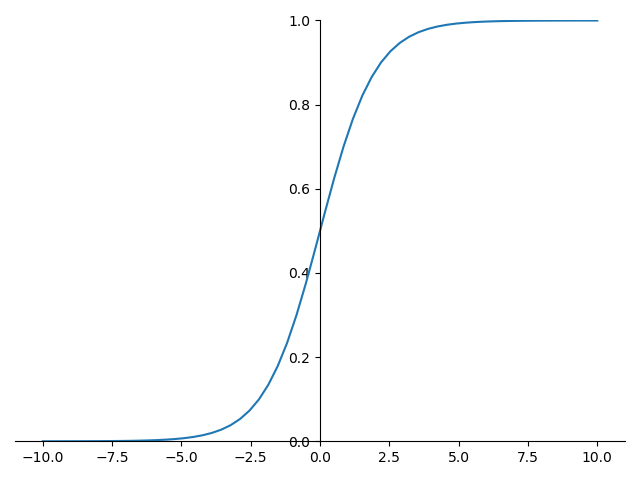
sigmoid 的导数图形如下：

sigmoid 优点：

• 能够把输入的连续值变换为0和1之间的输出 (可以看成概率)。
• 如果是非常大的负数或者正数作为输入的话，其输出分别为0或1，即输出对输入比较不敏感，参数更新比较稳定。

sigmoid 缺点：

• 在深度神经网络反向传播梯度时容易产生梯度消失（大概率）和梯度爆炸（小概率）问题。根据求导的链式法则，我们都知道一般神经网络损失对于参数的求导涉及一系列偏导以及权重连乘，那连乘会有什么问题呢？如果随机初始化各层权重都小于1（注意到以上sigmoid导数不超过0.25，也是一个比较小的数），即各个连乘项都很小的话，接近0，那么最终很多很多连乘（对应网络中的很多层）会导致最终求得梯度为0，这就是梯度消失现象（大概率发生）。同样地，如果我们随机初始化权重都大于1（非常大）的话，那么一直连乘也是可能出现最终求得的梯度非常非常大，这就是梯度爆炸现象（很小概率发生）。
• sigmoid函数的输出是0到1之间的，并不是以0为中心的（或者说不是关于原点对称的）。这会导致什么问题呢？神经网络反向传播过程中各个参数w的更新方向（是增加还是减少）是可能不同的，这是由各层的输入值x决定的（为什么呢？推导详见）。有时候呢，在某轮迭代，我们需要一个参数w0增加，而另一个参数w1减少，那如果我们的输入都是正的话（sigmoid的输出都是正的，会导致这个问题），那这两个参数在这一轮迭代中只能都是增加了，这势必会降低参数更新的收敛速率。当各层节点输入都是负数的话，也如上分析，即所有参数在这一轮迭代中只能朝同一个方向更新，要么全增要么全减。（但是一般在神经网络中都是一个batch更新一次，一个batch中输入x有正有负，是可以适当缓解这个情况的）
• sigmoid涉及指数运算，计算效率较低。

(2) tanh 函数

tanh是双曲正切函数。（一般二分类问题中，隐藏层用tanh函数，输出层用sigmod函数，但是随着Relu的出现所有的隐藏层基本上都使用relu来作为激活函数了）

tanh 的函数公式如下：

\[tanh(x) = {exp(x)-exp(-x) \over exp(x)+exp(-x) }
\]

其导数也具备同sigmoid导数类似的性质，导数公式如下：

\[tanh'(x) = 1 - tanh^2(x)
\]

tanh 的函数图形如下：



tanh 的导数图形如下：



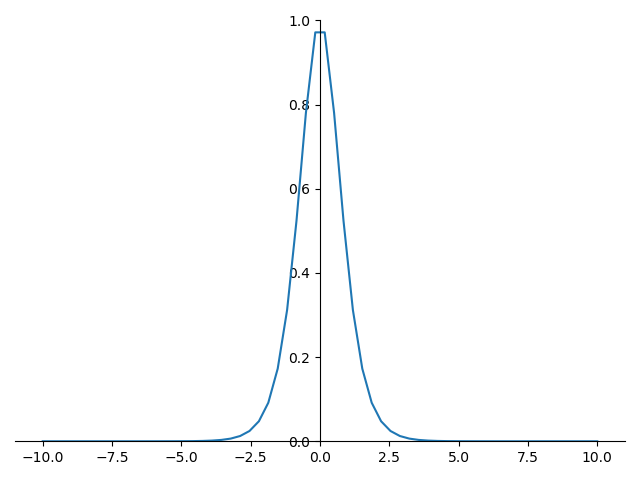
tanh 优点：

• 输出区间在(-1,1)之间，且输出是以0为中心的，解决了sigmoid的第二个问题。
• 如果使用tanh作为激活函数，还能起到归一化（均值为0）的效果。

tanh 缺点：

• 梯度消失的问题依然存在（因为从导数图中我们可以看到当输入x偏离0比较多的时候，导数还是趋于0的）。
• 函数公式中仍然涉及指数运算，计算效率偏低。

(3) ReLU 函数

ReLU (Rectified Linear Units) 修正线性单元。ReLU目前仍是最常用的activation function，在隐藏层中推荐优先尝试！

ReLU 的函数公式如下：

\[ReLU = max(0,x)
\]

ReLU 的函数图形如下：



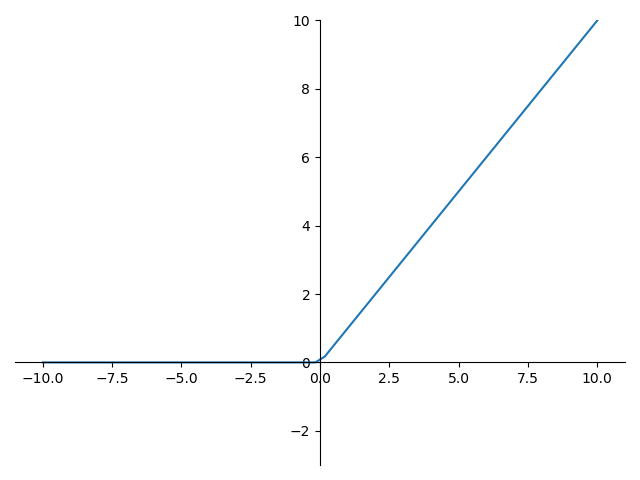
ReLU 的导数图形如下：



ReLU 优点：

• 梯度计算很快，只要判断输入是否大于0即可，这一点加快了基于梯度的优化算法的计算效率，收敛速度远快于Sigmoid和tanh。
• 在正区间上解决了梯度消失（因为梯度永远为1，不会连乘等于0）的问题。

ReLU 缺点：

• ReLU 的输出不是以0为中心的，但是这点可以通过一个batch更新一次参数来缓解。
• Exist Dead ReLU Problem，某些神经元存在死机的问题（永远不会被激活），这是由于当输入x小于0的时候梯度永远为0导致的，梯度为0代表参数不更新（加0减0），这个和sigmoid、tanh存在一样的问题，即有些情况下梯度很小很小很小，梯度消失。但是实际的运用中，该缺陷的影响不是很大。 因为比较难发生，为什么呢？因为这种情况主要有两个原因导致，其一：非常恰巧的参数初始化。神经元的输入为加权求和，除非随机初始化恰好得到了一组权值参数使得加权求和变成负数，才会出现梯度为0的现象，然而这个概率是比较低的。其二：学习率设置太大，使得某次参数更新的时候，跨步太大，得到了一个比原先更差的参数。选择已经有一些参数初始化的方法以及学习率自动调节的算法可以防止出现上述情况。（具体方法笔者暂时还未了解！了解了之后再进行补充）

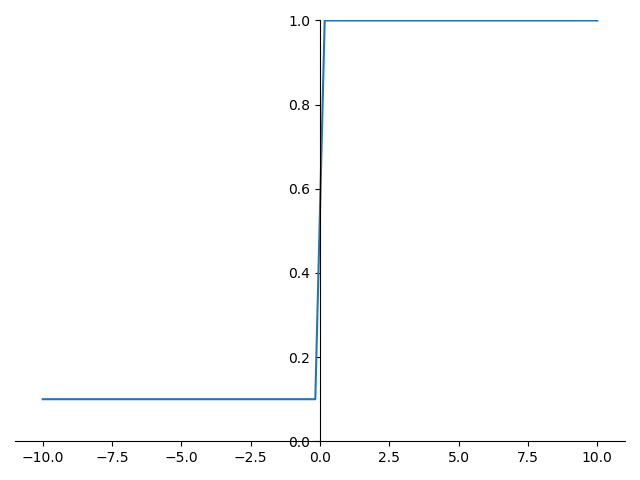
(4) Leaky Relu 函数（PRelu）

Leaky Relu 的函数公式如下：

\[PRelu(α,x)=max(αx,x)
\]

以下以α为0.1的情况为例，通常α=0.01，这边取0.1只是为了图形梯度大一点，画出来比较直观。

Leaky Relu 的函数图形如下：



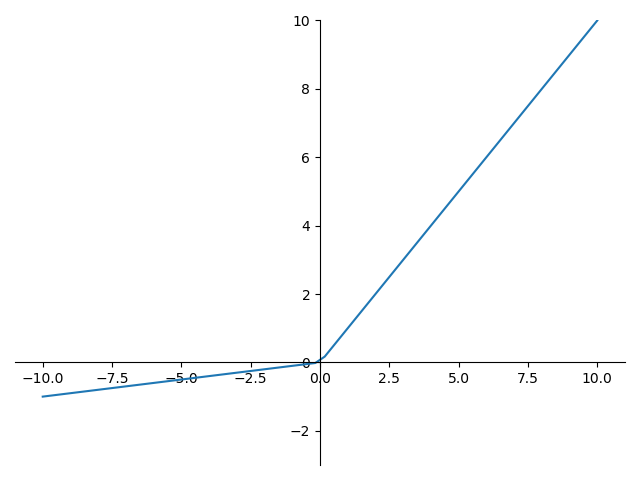
Leaky Relu 的导数图形如下：



Leaky Relu 优点：

• 解决了relu函数输入小于0时梯度为0的问题。
• 与ReLU一样梯度计算快，是常数，只要判断输入大于0还是小于0即可。

对于Leaky Relu 的缺点笔者暂时不了解，但是实际应用中，并没有完全证明Leaky ReLU总是好于ReLU，因此ReLU仍是最常用的激活函数。

---

本文参考-1

本文参考-2

本文参考-3